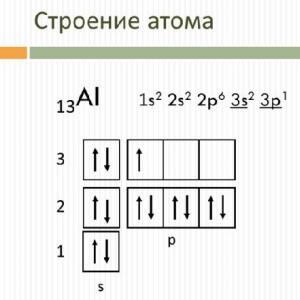
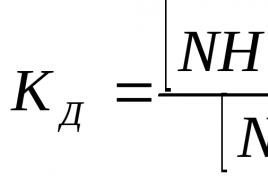Jeden a 0 pythagorejských nohavíc. Rôzne spôsoby dokázania Pytagorovej vety: príklady, popisy a recenzie

V jednej veci si môžete byť stopercentne istí, že na otázku, aký je štvorec prepony, odpovedá každý dospelý odvážne: „Súčet štvorcov nôh.“ Táto veta je pevne zakorenená v mysliach každého vzdelaného človeka, ale stačí niekoho požiadať, aby to dokázal, a potom môžu nastať ťažkosti. Preto si pripomeňme a zvážime rôzne spôsoby dokazovania Pytagorovej vety.

Stručný životopis

Pytagorovu vetu pozná takmer každý, ale z nejakého dôvodu nie je biografia osoby, ktorá ju narodila, taká populárna. Toto je opraviteľné. Preto predtým, ako začnete študovať rôzne spôsoby dokazovania Pytagorovej vety, musíte sa v krátkosti oboznámiť s jeho osobnosťou.

Pythagoras je filozof, matematik, mysliteľ pôvodne z roku Dnes je veľmi ťažké odlíšiť jeho biografiu od legiend, ktoré sa sformovali na pamiatku tohto velikána. Ako ale vyplýva zo spisov jeho nasledovníkov, Pythagoras zo Samosu sa narodil na ostrove Samos. Jeho otec bol obyčajný rezač kameňa, ale jeho matka pochádzala zo šľachtickej rodiny.

Podľa legendy pôrod Pytagoriády predpovedala žena menom Pythia, na počesť ktorej bol chlapec pomenovaný. Podľa jej predpovede mal narodený chlapec ľudstvu priniesť veľa výhod a dobroty. Čo vlastne urobil.

Zrod teorémy

V mladosti sa Pythagoras presťahoval do Egypta, aby sa tam stretol so slávnymi egyptskými mudrcami. Po stretnutí s nimi bol prijatý na štúdium, kde sa dozvedel všetky veľké úspechy egyptskej filozofie, matematiky a medicíny.

Pravdepodobne to bolo v Egypte, keď sa Pytagoras inšpiroval majestátom a krásou pyramíd a vytvoril svoju veľkú teóriu. To môže čitateľov šokovať, ale moderní historici sa domnievajú, že Pytagoras svoju teóriu nedokázal. Svoje vedomosti odovzdával iba svojim nasledovníkom, ktorí neskôr dokončili všetky potrebné matematické výpočty.

Nech je to už akokoľvek, dnes nie je známy jeden spôsob dokázania tejto vety, ale hneď niekoľko. Dnes zostáva len hádať, ako presne starí Gréci vykonali svoje výpočty, takže tu zvážime rôzne spôsoby dokázania Pytagorovej vety.

Pytagorova veta

Pred začatím akýchkoľvek výpočtov musíte zistiť, ktorá teória sa má dokázať. Pytagorova veta znie takto: "V trojuholníku, v ktorom je jeden z uhlov 90 o, sa súčet štvorcov nôh rovná štvorcu prepony."

Celkovo existuje 15 rôznych spôsobov, ako dokázať Pytagorovu vetu. Toto je dosť veľká postava, venujme preto pozornosť najobľúbenejším z nich.

Metóda jedna

Najskôr si poďme určiť, čo sa nám dáva. Tieto údaje budú platiť aj pre ďalšie metódy dokazovania Pytagorovej vety, takže by ste si mali okamžite zapamätať všetky dostupné notácie.

Povedzme, že je daný pravouhlý trojuholník s nohami a, b a preponou rovnou c. Prvá metóda dokazovania je založená na skutočnosti, že štvorec musí byť nakreslený z pravouhlého trojuholníka.

Aby ste to dosiahli, musíte nakresliť segment rovný nohe b k nohe dĺžky a a naopak. Toto by malo robiť dva rovnaké strany námestie. Zostáva iba nakresliť dve rovnobežné čiary a štvorec je pripravený.

Vo vnútri výsledného obrázku musíte nakresliť ďalší štvorec so stranou rovnajúcou sa prepočtu pôvodného trojuholníka. Za týmto účelom musíte z vrcholov ac a sv nakresliť dva rovnobežné segmenty rovné c. Získame teda tri strany štvorca, z ktorých jedna je prepona pôvodného pravouhlého trojuholníka. Zostáva len dokončiť štvrtý segment.

Na základe výsledného obrázku môžeme konštatovať, že plocha vonkajšieho štvorca je (a + b) 2. Ak sa pozriete dovnútra figúry, uvidíte, že okrem vnútorného štvorca obsahuje štyri pravouhlé trojuholníky. Plocha každého z nich je 0,5 av.

Preto je táto oblasť: 4 * 0,5av + s 2 \u003d 2av + s 2

Preto (a + b) 2 \u003d 2ab + c 2

A preto c 2 \u003d a 2 + b 2

Veta je dokázaná.

Druhá metóda: podobné trojuholníky

Tento vzorec pre dôkaz Pytagorovej vety bol odvodený na základe výroku z časti o geometrii o podobných trojuholníkoch. Hovorí sa v ňom, že rameno pravouhlého trojuholníka je proporcionálnym priemerom jeho prepočtu a segmentom prepočtu vychádzajúcim z vrcholu uhla 90 °.

Počiatočné údaje zostávajú nezmenené, začnime teda hneď s dôkazom. Nakreslíme segment SD kolmo na stranu AB. Na základe vyššie uvedeného tvrdenia sú nohy trojuholníkov:

AC \u003d √AB * HELL, SV \u003d √AB * DV.

Aby sme odpovedali na otázku, ako dokázať Pytagorovu vetu, musí byť dôkaz doplnený druhou mocninou oboch nerovností.

AC 2 \u003d AB * HELL a SV 2 \u003d AB * DV

Teraz musíte spočítať výsledné nerovnosti.

AC 2 + SV 2 \u003d AB * (BP * DV), kde BP + DV \u003d AB

Ukázalo sa, že:

AC 2 + SV 2 \u003d AB * AB

A preto:

AC 2 + CB 2 \u003d AB 2

Dôkaz Pytagorovej vety a rôzne spôsoby jej riešenia si vyžadujú všestranný prístup k tomuto problému. Táto možnosť je však jednou z najjednoduchších.

Ďalšia technika výpočtu

Opis rôznych metód dokazovania Pytagorovej vety nemusí hovoriť nič, kým nezačneš cvičiť sám. Mnoho techník zahŕňa nielen matematické výpočty, ale aj zostrojenie nových čísel z pôvodného trojuholníka.

V tomto prípade je potrebné z nohy BC dokončiť ďalší pravouhlý trojuholník VSD. Teraz teda existujú dva trojuholníky so spoločnou nohou BC.

S vedomím, že oblasti týchto obrázkov majú pomer ako štvorce ich podobných lineárnych rozmerov, potom:

S avd * s 2 - S avd * a 2 \u003d S avd * a 2 - S awd * a 2

S abc * (s 2 -v 2) \u003d a 2 * (S abd -S vd)

s 2-v 2 \u003d a 2

c 2 \u003d a 2 + b 2

Pretože táto možnosť je ťažko vhodná z rôznych metód dokazovania Pytagorovej vety pre 8. ročník, môžete použiť nasledujúcu techniku.

Najjednoduchší spôsob, ako dokázať Pytagorovu vetu. Recenzie

Historici sa domnievajú, že táto metóda bola prvýkrát použitá na dokázanie vety ešte v starovekom Grécku. Je to najjednoduchší, pretože nevyžaduje absolútne žiadne výpočty. Ak nakreslíte postavu správne, bude zreteľne viditeľný dôkaz o tom, že 2 + v 2 \u003d c 2.

Podmienky pre túto metódu sa budú mierne líšiť od predchádzajúcej. Na dokázanie vety predpokladajme, že pravouhlý trojuholník ABC je rovnoramenný.

Vezmeme AC preponu ako stranu štvorca a rozdelíme jeho tri strany. Vo výslednom štvorci musíte navyše nakresliť dve diagonálne čiary. Takže vnútri sú štyri rovnoramenné trojuholníky.

K nohám AB a CB musíte tiež nakresliť štvorec a do každej z nich nakresliť jednu diagonálnu čiaru. Prvý riadok je nakreslený z vrcholu A, druhý z C.

Teraz sa musíte podrobne pozrieť na výsledný výkres. Pretože na AC prepone sú štyri trojuholníky, ktoré sa rovnajú pôvodnému, a na nohách dva, hovorí to o pravdivosti tejto vety.

Mimochodom, vďaka tejto metóde dokazovania Pytagorovej vety sa zrodila slávna fráza: „ Pytagorove nohavice vo všetkých smeroch sú si rovní. ““

Dôkaz J. Garfielda

James Garfield je 20. prezidentom Spojených štátov amerických. Okrem toho, že zanechal svoju stopu v dejinách ako vládca USA, bol tiež nadaným samoukom.

Na začiatku svojej kariéry bol radovým učiteľom v ľudovej škole, čoskoro sa však stal riaditeľom jednej z vysokých škôl. Túžba po sebarozvoji mu umožnila navrhnúť novú teóriu na dokázanie Pytagorovej vety. Veta a príklad jej riešenia sú nasledujúce.

Najskôr musíte na list papiera nakresliť dva pravouhlé trojuholníky, aby noha jedného z nich bola pokračovaním druhého. Vrcholy týchto trojuholníkov musia byť spojené, aby nakoniec vytvorili lichobežník.

Ako viete, plocha lichobežníka sa rovná súčinu polovičného súčtu jeho základov a výšky.

S \u003d a + b / 2 * (a + b)

Ak výsledný lichobežník považujeme za útvar pozostávajúci z troch trojuholníkov, potom jeho plochu nájdeme takto:

S \u003d av / 2 * 2 + s 2/2

Teraz musíte vyrovnať dva pôvodné výrazy

2av / 2 + s / 2 \u003d (a + b) 2/2

c 2 \u003d a 2 + b 2

O Pytagorovej vete a metódach jej dôkazu možno napísať viac ako jeden diel. Má však zmysel, keď sa tieto vedomosti nedajú uplatniť v praxi?

Praktická aplikácia Pytagorovej vety

Bohužiaľ, v modernej školské programy použitie tejto vety je uvedené iba v geometrických úlohách. Absolventi čoskoro opustia múry školy a nikdy nevedia, ako môžu svoje vedomosti a zručnosti uplatniť v praxi.

V skutočnosti použite Pythagorovu vetu vo vašom každodenný život kazdy moze. A nielen v profesionálna činnosť, ale aj v bežných domácich prácach. Uvažujme o niekoľkých prípadoch, keď môže byť Pytagorova veta a metódy jej dôkazu mimoriadne potrebné.

Súvislosť medzi vetou a astronómiou

Zdalo by sa, ako môžu byť hviezdy a trojuholníky na papieri spojené. Astronómia je v skutočnosti vedný odbor, v ktorom sa široko používa Pytagorova veta.

Zvážte napríklad pohyb svetelného lúča v priestore. Je známe, že svetlo sa pohybuje v oboch smeroch rovnakou rýchlosťou. Nazýva sa trajektória AB, ktorou sa pohybuje svetelný lúč l. A polovicu času, ktorý trvá svetlo, kým sa dostaneme z bodu A do bodu B, zavoláme t... A rýchlosť lúča - c. Ukázalo sa, že: c * t \u003d l

Ak sa pozriete na tento veľmi lúč z inej roviny, napríklad z vesmírnej lode, ktorá sa pohybuje rýchlosťou v, potom sa pri takomto pozorovaní telies zmení ich rýchlosť. V takom prípade sa aj stacionárne prvky budú pohybovať s rýchlosťou v v opačnom smere.

Povedzme, že komická línia sa plaví vpravo. Potom sa body A a B, medzi ktorými sa lúč odhodí, presunú doľava. Navyše, keď sa lúč pohybuje z bodu A do bodu B, bod A má čas sa pohybovať a podľa toho už svetlo dorazí do nového bodu C. Ak chcete zistiť polovicu vzdialenosti, o ktorú sa posunul bod A, musíte vynásobiť rýchlosť vložky polovicou doby jazdy lúča (t „).

Ak chcete zistiť, akú veľkú vzdialenosť môže lúč svetla v tomto období prejsť, musíte označiť polovicu cesty novými písmenami s a získať nasledujúci výraz:

Ak si predstavíme, že body svetla C a B, rovnako ako vesmírna vložka, sú vrcholy rovnoramenného trojuholníka, potom segment z bodu A do vložky ju rozdelí na dva pravouhlé trojuholníky. Preto vďaka Pytagorovej vete nájdete vzdialenosť, ktorú by mohol lúč svetla prejsť.

Tento príklad samozrejme nie je najúspešnejším príkladom, pretože iba pár ľudí môže mať šťastie, aby si to vyskúšali v praxi. Preto zvážime pozemskejšie aplikácie tejto vety.

Polomer prenosu mobilného signálu

Moderný život si už nemožno predstaviť bez existencie inteligentných telefónov. Boli by však veľmi užitočné, keby sa nemohli spojiť s predplatiteľmi prostredníctvom mobilnej komunikácie?!

Kvalita mobilnej komunikácie priamo závisí od výšky antény mobilného operátora. Ak chcete vypočítať, ako ďaleko dokáže telefón prijať signál z mobilnej veže, môžete použiť Pytagorovu vetu.

Povedzme, že musíte nájsť približnú výšku stacionárnej veže, aby mohla šíriť signál v okruhu 200 kilometrov.

AB (výška veže) \u003d x;

Lietadlo (polomer prenosu signálu) \u003d 200 km;

OS (polomer zemegule) \u003d 6380 km;

OB \u003d OA + ABOV \u003d r + x

Pomocou Pytagorovej vety sme zistili, že minimálna výška veže by mala byť 2,3 kilometra.

Pytagorova veta v každodennom živote

Pytagorova veta je čudná, môže byť užitočná aj v každodenných veciach, napríklad pri určovaní výšky šatníka. Na prvý pohľad nie je potrebné používať také zložité výpočty, pretože merania môžete jednoducho vykonať pomocou pásky. Ale mnohí sa čudujú, prečo počas procesu montáže vznikajú určité problémy, ak boli všetky merania urobené viac než presne.

Faktom je, že šatníková skriňa je zostavená vo vodorovnej polohe a až potom sa zdvihne a namontuje sa na stenu. Preto by strana skrinky v procese zdvíhania konštrukcie mala prechádzať voľne tak vo výške, ako aj v uhlopriečke miestnosti.

Predpokladajme, že máte šatníkovú skriňu s hĺbkou 800 mm. Vzdialenosť od podlahy k stropu - 2 600 mm. Skúsený výrobca nábytku vám povie, že výška skrinky by mala byť o 126 mm menšia ako výška miestnosti. Prečo však presne 126 mm? Pozrime sa na príklad.

Pri ideálnych rozmeroch skrinky kontrolujeme činnosť Pytagorovej vety:

AC \u003d √AB 2 + √BC 2

AC \u003d √ 2474 2 +800 2 \u003d 2600 mm - všetko sa spája.

Povedzme, že výška skrinky nie je 2474 mm, ale 2505 mm. Potom:

AC \u003d √2505 2 + √800 2 \u003d 2629 mm.

Preto nie je táto skrinka vhodná na inštaláciu v tejto miestnosti. Pretože jeho zdvihnutie do zvislej polohy môže poškodiť jeho telo.

Možno, keď zvážime rôzne spôsoby dokazovania Pytagorovej vety rôznymi vedcami, môžeme dospieť k záveru, že je to viac ako pravda. Teraz môžete použiť informácie prijaté vo vašom každodennom živote a byť si úplne istí, že všetky výpočty budú nielen užitočné, ale aj správne.

»Významný profesor matematiky na univerzite vo Warwicku, slávny popularizátor vedy Ian Stewart, ktorý sa venuje úlohe čísel v dejinách ľudstva a dôležitosti ich štúdia v našej dobe.

Pytagorova prepona

Pytagorove trojuholníky majú pravý uhol a celé číslo. Najjednoduchší z nich má najdlhšiu stranu dĺžky 5, zvyšok - 3 a 4. Existuje celkom 5 pravidelných mnohostenov. Rovnicu piateho stupňa nie je možné vyriešiť pomocou koreňov piateho stupňa - ani iných koreňov. Mriežky v rovine a v trojrozmernom priestore nemajú päťlalokovú symetriu rotácie, preto také symetrie absentujú ani v kryštáloch. Možno ich však nájsť v mriežkach v štvorrozmernom priestore a v zaujímavých štruktúrach známych ako kvázikryštály.

Hypotenáza najmenšieho pytagorejského trojčaťa

Pytagorova veta hovorí, že najdlhšia strana pravého trojuholníka (povestná prepona) súvisí s ostatnými dvoma stranami tohto trojuholníka veľmi jednoducho a nádherne: štvorec prepony sa rovná súčtu štvorcov ostatných dvoch strán.

Tradične túto vetu nazývame Pythagoras, ale jej história je v skutočnosti dosť nejasná. Hlinené tablety naznačujú, že starí Babylončania poznali Pytagorovu vetu dávno pred samotným Pytagorasom; slávu objaviteľa mu priniesol matematický kult Pytagorejcov, ktorých priaznivci verili, že vesmír je založený na numerických zákonoch. Starovekí autori pripisovali Pytagorejčanom - a teda Pytagorovi - rôzne matematické vety, ale v skutočnosti vôbec netušíme, čo matematika Pythagoras sám robil. Ani nevieme, či by Pytagorovci mohli dokázať Pytagorovu vetu, alebo či jednoducho verili, že je to pravda. Alebo s najväčšou pravdepodobnosťou mali presvedčivé dôkazy o jej pravdivosti, ktoré by však nestačili na to, čo dnes považujeme za dôkaz.

Dôkazy Pytagoriády

Prvý známy dôkaz Pytagorovej vety nájdeme v Euklidových prvkoch. Toto je dosť komplikovaný dôkaz pomocou kresby, na ktorej viktoriánski školáci okamžite rozpoznajú „Pytagorove nohavice“; kresba skutočne pripomína spodky, ktoré sa sušia na lane. Existujú doslova stovky ďalších dôkazov, z ktorých väčšina zvyšuje zreteľnosť tvrdenia.

// Obr. 33. Pytagorove nohavice

Jedným z najjednoduchších dôkazov je druh matematickej hádanky. Vezmite ľubovoľný pravý trojuholník, vytvorte z neho štyri kópie a zhromaždite ich vo vnútri štvorca. Pri jednom stohovaní vidíme štvorec na preponu; na druhej strane štvorce na ostatných dvoch stranách trojuholníka. Zároveň je zrejmé, že oblasti sú v obidvoch prípadoch rovnaké.

// Obr. 34. Vľavo: štvorec na preponu (plus štyri trojuholníky). Vpravo: súčet štvorcov na ostatných dvoch stranách (plus rovnaké štyri trojuholníky). Teraz vylúčte trojuholníky

Perigalova pitva je ďalšou dôkazovou hádankou.

// Obr. 35. Pitva Perigale

Existuje aj dôkaz o vete, ktorá používa štvorce v rovine. Asi takto objavili túto vetu Pytagorejci alebo ich neznámi predchodcovia. Ak sa pozriete na to, ako šikmý štvorec prekrýva dva ďalšie štvorce, uvidíte, ako rozrezať veľký štvorec na kúsky a potom ich zložiť na dva menšie štvorce. Môžete tiež vidieť pravouhlé trojuholníky, ktorých strany dávajú rozmery troch zapojených štvorcov.

// Obr. 36. Dlažobný dôkaz

Existujú zaujímavé dôkazy o použití podobných trojuholníkov v trigonometrii. Je známych najmenej päťdesiat rôznych dôkazov.

Pytagorejské trojčatá

V teórii čísel sa Pytagorova veta stala zdrojom plodnej myšlienky: nájsť celočíselné riešenia algebraických rovníc. Pytagorova trojka je množina celých čísel a, b a c taká, že

Geometricky táto trojka definuje pravouhlý trojuholník s celočíselnými stranami.

Najmenšia prepona Pytagorovej trojice je 5.

Ďalšie dve strany tohto trojuholníka sú 3 a 4. Tu

32 + 42 = 9 + 16 = 25 = 52.

Ďalšia najväčšia prepona je 10, pretože

62 + 82 = 36 + 64 = 100 = 102.

Jedná sa však v podstate o ten istý trojuholník so zdvojenými stranami. Ďalšia najväčšia a skutočne odlišná prepona je pre ňu 13

52 + 122 = 25 + 144 = 169 = 132.

Euclid vedel, že existuje nekonečné množstvo rôznych variantov pytagorejských trojčiat, a uviedol, čo sa dá nazvať vzorcom, ako ich nájsť všetky. Neskôr Diophantus z Alexandrie navrhol jednoduchý recept, ktorý sa v zásade zhoduje s euklidovským.

Vezmite ľubovoľné dve prirodzené čísla a vypočítajte:

ich zdvojnásobená práca;

rozdiel medzi ich štvorcami;

súčet ich štvorcov.

Tri výsledné čísla budú strany Pytagorovho trojuholníka.

Vezmime si napríklad čísla 2 a 1. Vypočítajte:

dvojitý výrobok: 2 × 2 × 1 \u003d 4;

rozdiel štvorcov: 22 - 12 \u003d 3;

súčet štvorcov: 22 + 12 \u003d 5,

a dostali sme slávny trojuholník 3-4-5. Ak vezmeme namiesto toho čísla 3 a 2, dostaneme:

dvojitý výrobok: 2 × 3 × 2 \u003d 12;

rozdiel štvorcov: 32 - 22 \u003d 5;

súčet štvorcov: 32 + 22 \u003d 13,

a dostaneme ďalší najslávnejší trojuholník 5 - 12 - 13. Pokúsme sa vziať čísla 42 a 23 a získať:

dvojitý produkt: 2 × 42 × 23 \u003d 1932;

rozdiel štvorcov: 422 - 232 \u003d 1235;

súčet štvorcov: 422 + 232 \u003d 2293,

o trojuholníku 1235-1932-2293 nikto nikdy nepočul.

Ale fungujú aj tieto čísla:

12352 + 19322 = 1525225 + 3732624 = 5257849 = 22932.

V pravidle Diophantine je ešte jedna vlastnosť, ktorá už bola naznačená: po prijatí troch čísel môžeme vziať ďalšie ľubovoľné číslo a všetky ich vynásobiť. Trojuholník 3–4–5 teda možno zmeniť na trojuholník 6–8–10 vynásobením všetkých strán číslom 2 alebo na trojuholník 15–20–25 vynásobením všetkého číslom 5.

Ak prejdeme na jazyk algebry, pravidlo má nasledujúcu formu: nech u, v a k sú prirodzené čísla. Potom pravouhlý trojuholník so stranami

2kuv a k (u2 - v2) má preponu

Existujú aj iné spôsoby, ako predstaviť hlavnú myšlienku, ale všetky sa redukujú na vyššie uvedený spôsob. Táto metóda umožňuje získať všetky Pytagorove trojčatá.

Pravidelná mnohostena

Pravidelných mnohostenov je presne päť. Pravidelný mnohosten (alebo mnohosten) je trojrozmerná postava s konečným počtom plochých plôch. Tváre sa zbiehajú navzájom na čiarach nazývaných hrany; hrany sa stretávajú v bodoch nazývaných vrcholy.

Vyvrcholením euklidovského „Počiatku“ je dôkaz, že môže existovať iba päť pravidelných mnohostenov, teda mnohostenov, v ktorých je každá tvár pravidelným mnohouholníkom (rovnaké strany, rovnaké uhly), všetky tváre sú identické a všetky vrcholy sú obklopené rovnakým počtom rovnako vzdialených tvárí. Tu je päť bežných mnohostenov:

štvorsten so štyrmi trojuholníkovými plochami, štyrmi vrcholmi a šiestimi okrajmi;

kocka alebo šesťuholník so 6 hranatými plochami, 8 vrcholmi a 12 hranami;

oktaédr s 8 trojuholníkovými plochami, 6 vrcholmi a 12 hranami;

dodecahedron s 12 päťuholníkovými plochami, 20 vrcholmi a 30 okrajmi;

ikosahedrón s 20 trojuholníkovými plochami, 12 vrcholmi a 30 okrajmi.

// Obr. 37. Päť pravidelných mnohostenov

Pravidelnú mnohostenu nájdete aj v prírode. V roku 1904 Ernst Haeckel publikoval kresby drobných organizmov známych ako rádiolariáni; mnohé z nich sa tvarom podobajú tým veľmi piatim pravidelným mnohostenom. Možno však trochu korigoval prírodu a kresby úplne neodrážajú tvar konkrétnych živých bytostí. Prvé tri štruktúry sú tiež pozorované v kryštáloch. Nenájdete dodecahedron a icosahedron v kryštáloch, hoci tam občas narazia nepravidelné dodecahedrony a icosahedrony. Pravé dodekaedóny sa môžu javiť ako kvázikryštály, ktoré sú vo všetkých ohľadoch podobné kryštálom, až na to, že ich atómy netvoria periodickú mriežku.

// Obr. 38. Haeckelove kresby: rádiolariáni vo forme pravidelných mnohostenov

// Obr. 39. Vývoj pravidelného mnohostenu

Môže byť zaujímavé vyrobiť modely pravidelných mnohostenov z papiera tak, že vopred vystrihneme množinu vzájomne prepojených tvárí - hovorí sa tomu rozkladajúci sa mnohosten; sken je preložený pozdĺž okrajov a zodpovedajúce okraje sú zlepené dohromady. Je užitočné pridať ďalšiu lepiacu podložku na jeden z okrajov každého takého páru, ako je to znázornené na obr. 39. Ak takáto oblasť nie je, môžete použiť lepiacu pásku.

Rovnica piateho stupňa

Na riešenie rovníc 5. stupňa neexistuje algebraický vzorec.

Všeobecne vyzerá rovnica piateho stupňa takto:

ax5 + bx4 + cx3 + dx2 + ex + f \u003d 0.

Problémom je nájsť vzorec pre riešenie takejto rovnice (môže mať až päť riešení). Skúsenosti s narábaním s kvadratickými a kubickými rovnicami, ako aj s rovnicami štvrtého stupňa naznačujú, že takýto vzorec by mal existovať pre rovnice piateho stupňa a teoreticky by sa v nich mali objaviť korene piateho, tretieho a druhého stupňa. Opäť môžeme s istotou predpokladať, že taký vzorec, ak existuje, bude veľmi, veľmi ťažký.

Tento predpoklad sa nakoniec ukázal ako nesprávny. V skutočnosti žiadny takýto vzorec neexistuje; aspoň neexistuje vzorec koeficientov a, b, c, d, e a f zostavený pomocou sčítania, odčítania, násobenia a delenia a extrakcie koreňov. Na čísle 5 je teda niečo veľmi zvláštne. Dôvody tohto neobvyklého správania piatich sú veľmi hlboké a trvalo dlho, kým sme im porozumeli.

Prvým znakom problému bolo, že bez ohľadu na to, ako veľmi sa matematici snažili nájsť taký vzorec, bez ohľadu na to, aký inteligentný sú, vždy zlyhali. Každý istý čas veril, že dôvody spočívajú v neuveriteľnej zložitosti vzorca. Verilo sa, že nikto jednoducho nemôže tejto algebre správne porozumieť. Niektorí matematici však začali časom pochybovať, že taký vzorec vôbec existuje, a v roku 1823 dokázal Niels Hendrik Abel dokázať opak. Takýto vzorec neexistuje. Krátko nato Evariste Galois našiel spôsob, ako určiť, či rovnica jedného alebo druhého stupňa - 5., 6., 7., všeobecne akýkoľvek - je riešiteľná pomocou tohto druhu vzorca.

Záver z toho všetkého je jednoduchý: číslo 5 je zvláštne. Algebraické rovnice môžete vyriešiť (pomocou korene n stupne pre rôzne hodnoty n) pre stupne 1, 2, 3 a 4, nie však pre 5. stupeň. Tu zjavný vzor končí.

Nie je prekvapením, že výkonové rovnice väčšie ako 5 sa správajú ešte horšie; spája sa s nimi najmä rovnaká ťažkosť: č všeobecné vzorce ich vyriešiť. To neznamená, že rovnice nemajú riešenie; to tiež neznamená, že je nemožné nájsť veľmi presné číselné hodnoty týchto riešení. Všetko je to o obmedzeniach tradičných nástrojov algebry. To pripomína nemožnosť trízania uhla pomocou pravítka a kompasu. Odpoveď existuje, ale uvedené metódy sú nedostatočné a neumožňujú vám určiť, o čo ide.

Kryštalografické obmedzenie

Kryštály v dvoch a troch rozmeroch nemajú 5-lúčovú rotačnú symetriu.

Atómy v kryštáli tvoria mriežku, to znamená štruktúru, ktorá sa periodicky opakuje v niekoľkých nezávislých smeroch. Napríklad vzor na tapete sa opakuje pozdĺž dĺžky role; navyše sa zvyčajne opakuje v horizontálnom smere, niekedy s posunom od jedného kusu tapety k ďalšiemu. V podstate je tapeta dvojrozmerný kryštál.

Existuje 17 druhov plochých tapiet (pozri kapitolu 17). Líšia sa typmi symetrie, teda spôsobmi, ako tuho posunúť vzor tak, aby presne ležal na sebe v pôvodnej polohe. Medzi typy symetrie patria najmä rôzne možnosti symetria otáčania, kde by sa mal výkres otáčať o určitý uhol okolo určitého bodu - stredu súmernosti.

Poradie rotácie symetrie je to, koľkokrát je možné telo otočiť do úplného kruhu, aby sa všetky podrobnosti výkresu vrátili do pôvodných polôh. Napríklad 90 ° rotácia je symetria rotácie 4. rádu *. Zoznam možných typov symetrie rotácie v kryštálovej mriežke opäť naznačuje, že číslo 5 je neobvyklé: nie je tam. K dispozícii sú možnosti so symetriou rotácie 2, 3, 4 a 6. rádu, ale žiadna tapeta nemá symetriu rotácie 5. rádu. Rotačná symetria rádu viac ako 6 v kryštáloch tiež neexistuje, ale prvé porušenie sekvencie stále nastáva pri čísle 5.

To isté sa deje s kryštalografickými systémami v trojrozmernom priestore. Tu sa mriežka opakuje v troch nezávislých smeroch. Existuje 219 rôznych typov symetrie, alebo 230, ak počítate zrkadlový odraz kresba ako jej samostatná verzia - napriek tomu, že v tomto prípade neexistuje zrkadlová symetria. Opäť sa pozorujú rotačné symetrie rádov 2, 3, 4 a 6, ale nie 5. Táto skutočnosť sa nazýva kryštalografické obmedzenie.

V štvorrozmernom priestore existujú mriežky so symetriou 5. rádu; všeobecne je pre mriežky dostatočne vysokých rozmerov možné akékoľvek vopred určené poradie symetrie otáčania.

// Obr. 40. Krištáľová bunka stolová soľ. Tmavé guľôčky predstavujú atómy sodíka, ľahké - atómy chlóru

Kvázikryštály

Aj keď rotačná symetria 5. rádu v 2D a 3D mriežkach nie je možná, môže existovať v o niečo menej pravidelných štruktúrach známych ako kvázikryštály. Roger Penrose pomocou Keplerových náčrtov objavil rovinné systémy so všeobecnejším typom päťnásobnej symetrie. Volajú sa kvázikryštály.

V prírode existujú kvázikryštály. V roku 1984 Daniel Shechtman zistil, že zliatina hliníka a mangánu môže vytvárať kvázikryštály; kryštalografi spočiatku jeho správu vítali s určitým skepticizmom, neskôr sa objav potvrdil a v roku 2011 bol ocenený Shekhtman nobelová cena v chémii. V roku 2009 objavil tím vedcov pod vedením Luka Bindiho kvázikryštály v mineráli z ruskej vysočiny Koryak - kombinácia hliníka, medi a železa. Dnes sa tento minerál nazýva ikosahedrit. Po zmeraní obsahu rôznych izotopov kyslíka v mineráli hmotnostným spektrometrom vedci preukázali, že tento minerál nepochádza zo Zeme. Vznikla asi pred 4,5 miliardami rokov, v čase, keď bola slnečná sústava ešte len v začiatkoch, a väčšinu času strávila v páse asteroidov obiehajúcich okolo Slnka, až kým nejaká porucha nezmenila jeho obežnú dráhu a nakoniec ju neviedla k Zem.

// Obr. 41. Vľavo: jedna z dvoch kvázikryštalických mriežok s päťnásobnou presnou symetriou. Vpravo: atómový model ikosaedrálneho kvázikryštálu hliníka, paládia a mangánu

Pythagorove nohavice Komický názov pre Pythagorovu vetu, ktorý vznikol vďaka tomu, že štvorce postavené po stranách obdĺžnika a rozchádzajúce sa v rôznych smeroch pripomínajú strih nohavíc. Miloval som geometriu ... a na prijímacej skúške na univerzitu som dostal dokonca pochvalu od Chumakova, profesora matematiky, za vysvetlenie vlastností rovnobežných čiar a Pytagorových nohavíc bez dosky, kreslenie rukami vzduchom. (N. Pirogov. Denník starého lekára).

Frazeologický slovník ruského spisovného jazyka. - M.: Astrel, AST... A.I. Fedorov. 2008.

Pozrite sa, čo je „Pythagorejské nohavice“ v iných slovníkoch:

Nohavice - získajte funkčný zľavový kupón SuperStep na Akademik alebo si kúpte lacné nohavice s dopravou zdarma v akcii na SuperStep

Pytagorove nohavice - ... Wikipedia

Pytagorove nohavice - Zharg. šk. Shuttle. Pytagorova veta, ktorou sa ustanovuje vzťah medzi oblasťami štvorcov vybudovaných na preponu a ramenami pravouhlého trojuholníka. BTS, 835 ... Veľký slovník ruských výrokov

pytagorove nohavice - Vtipný názov Pytagorovej vety, ktorá ustanovuje vzťah medzi plochami štvorcov postavených na preponu a nohami pravého trojuholníka, ktoré na obrázkoch vyzerajú ako strih nohavíc ... Slovník mnohých výrazov

pythagorovské nohavice (líčenie) - poznámka pod čiarou: o nadanej osobe Porov. Toto je nepochybný mudrc. V staroveku by pravdepodobne vynašiel Pytagorejské nohavice ... Saltykov. Farebné písmená. Pytagorove nohavice (geom.): V obdĺžniku sa štvorec prepony rovná štvorcom nôh (doktrína ... Michelsonov veľký vysvetľujúci frazeologický slovník

Pytagorejské nohavice sú si rovnaké zo všetkých strán - Počet tlačidiel je známy. Prečo je vták stiesnený? (zhruba) o nohaviciach a mužských genitáliách. Pytagorejské nohavice sú si rovnaké zo všetkých strán. Aby sme to dokázali, je potrebné odstrániť a ukázať 1) o Pytagorovej vete; 2) o širokých nohaviciach ... Živá reč. Slovník hovorových výrazov

Pytagorejské nohavice tvoria - Piѳagorovove nohavice (vymyslieť) ponožku. o nadanom človeku. St Toto je nepochybný mudrc. V staroveku by pravdepodobne vymyslel Piѳagorove nohavice ... Saltykov. Motley písmená. Piѳagorovove nohavice (geom.): V štvorcovom štvorci prepony ... ... Michelsonov veľký vysvetľujúci frazeologický slovník (pôvodný pravopis)

Pytagorejské nohavice sú si vo všetkých smeroch rovnaké - Vtipný dôkaz Pytagorovej vety; tiež žartujem o kamarátových vrecovitých nohaviciach ... Slovník ľudovej frazeológie

Napr. Hrubý ...

PYTHAGOROVE NOHAVICE SÚ ROVNAKÉ Z VŠETKÝCH STRÁN (POČET TLAČÍTOK JE ZNAM. PREČO JE TAKÉ TESNO? - príd. hrubý ... Vysvetľujúci slovník moderných hovorových frazeologických jednotiek a porekadiel

nohavice - podstatné meno, množné číslo, uptr. por. často Morfológia: pl. čo? nohavice, (nie) čo? nohavice, preco? nohavice, (pozri) čo? nohavice čo? nohavice o čom? o nohaviciach 1. Nohavice sú odev, ktorý má dve krátke alebo dlhé nohy a zakrýva spodnú časť ... ... Dmitrievov vysvetľujúci slovník

Knihy

• Pytagorove nohavice ,. V tejto knihe nájdete fantasy a dobrodružstvo, zázraky a beletriu. Vtipné i smutné, obyčajné i tajomné ... Čo ďalšie je potrebné na zábavné čítanie? Hlavná vec je mať ...

Rímsky architekt Vitruvius vyzdvihol Pytagorovu vetu „z početných objavov, ktoré poskytovali služby pre rozvoj ľudského života“, a vyzval k jej maximálnemu rešpektu. Bolo to späť v 1. storočí pred naším letopočtom. e. Na prelome 16. - 17. storočia ho slávny nemecký astronóm Johannes Kepler označil za jeden z pokladov geometrie, porovnateľných s mierou zlata. Je nepravdepodobné, že vo všetkej matematike bude závažnejšie a významnejšie tvrdenie, pretože z hľadiska počtu vedeckých a praktických aplikácií nie je Pytagorova veta rovnocenná.

Pytagorova veta pre prípad rovnoramenného pravouhlého trojuholníka.

Veda a život // Ilustrácie

Ilustrácia k Pytagorovej vete z „Pojednania o merajúcom póle“ (Čína, 3. storočie pred n. L.) A na jej základe zrekonštruovaný dôkaz.

Veda a život // Ilustrácie

S. Perkins. Pytagoras.

Plán možného dôkazu Pytagoriády.

„Mosaic of Pythagoras“ a an-Nayriziho obklad troch štvorcov na dôkaz Pytagorovej vety.

P. de Hooch. Na nádvorí hosteska a slúžka. Okolo roku 1660.

J. Ohtervelt. Blúdiaci hudobníci pred dverami bohatého domu. 1665 rokov.

Pytagorove nohavice

Pytagorova veta je možno najznámejšou a nepochybne najslávnejšou v dejinách matematiky. V geometrii sa používa doslova na každom kroku. Napriek jednoduchosti jej formulovania nie je táto veta v žiadnom prípade zrejmá: pohľad na pravouhlý trojuholník so stranami a< b < c, усмотреть соотношение a 2 + b 2 = c 2 невозможно. Однажды известный американский логик и популяризатор науки Рэймонд Смаллиан, желая подвести учеников к открытию теоремы Пифагора, начертил на доске прямоугольный треугольник и по квадрату на каждой его стороне и сказал: «Представьте, что эти квадраты сделаны из кованого золота и вам предлагают взять себе либо один большой квадрат, либо два маленьких. Что вы выберете?» Мнения разделились пополам, возникла оживлённая дискуссия. Каково же было удивление учеников, когда учитель объяснил им, что никакой разницы нет! Но стоит только потребовать, чтобы катеты были равны, - и утверждение теоремы станет явным (рис. 1). И кто после этого усомнится, что «пифагоровы штаны» во все стороны равны? А вот те же самые «штаны», только в «сложенном» виде (рис. 2). Такой чертёж использовал герой одного из диалогов Платона под названием «Менон», знаменитый философ Сократ, разбирая с мальчиком-рабом задачу на построение квадрата, площадь которого в два раза больше площади данного квадрата. Его рассуждения, по сути, сводились к доказательству теоремы Пифагора, пусть и для конкретного треугольника.

Obrázky zobrazené na obr. 1 a 2 pripomínajú najjednoduchší ornament štvorcov a ich rovnakých častí - geometrický vzor známy od nepamäti. Môžu úplne zakryť lietadlo. Matematik by také zakrytie lietadla nazval mnohouholníkmi parketami alebo obkladmi. Čo s tým má Pythagoras spoločné? Ukazuje sa, že ako prvý vyriešil problém správnych parkiet, ktorý začal so štúdiom obkladov. rôzne povrchy... Pythagoras teda ukázal, že rovinu okolo bodu možno pokryť bez medzier iba rovnakými pravidelnými polygónmi tri typy: šesť trojuholníkov, štyri štvorce a tri šesťuholníky.

O 4000 rokov neskôr

História Pytagorovej vety siaha do staroveku. Spomína sa to v babylonských textoch klinového písma z čias kráľa Hammurabiho (XVIII. Storočie pred n. L.), Teda 1200 rokov pred narodením Pytagorasa. Veta bola použitá ako hotové pravidlo pri mnohých problémoch, najjednoduchšie je nájsť uhlopriečku štvorca po jeho boku. Je možné, že Babylončania dostali pomer a 2 + b 2 \u003d c 2 pre ľubovoľný pravouhlý trojuholník jednoduchým „zovšeobecnením“ rovnosti a 2 + a 2 \u003d c 2. Ale je im to odpustiteľné - pre praktickú geometriu starých ľudí, ktorá sa zredukovala na merania a výpočty, nebolo potrebné nijaké dôsledné odôvodnenie.

Teraz, takmer o 4000 rokov neskôr, máme do činenia s vetou, ktorá drží rekord v počte možných dôkazov. Mimochodom, ich zber je dlhou tradíciou. Vrchol záujmu o Pytagorovu vetu padol na druhú polovica XIX - začiatok XX storočia. A ak prvé zbierky neobsahovali viac ako dva alebo tri desiatky dôkazov, potom sa na konci 19. storočia ich počet priblížil k stovke a po ďalšom polstoročí presiahol 360, a to sú len tie, ktoré boli zozbierané z rôznych zdrojov. Kto neprijal riešenie tejto nestarnúcej úlohy - od významných vedcov a popularizátorov vedy až po kongresmanov a školákov. A čo je pozoruhodné, v originalite a jednoduchosti riešenia neboli niektorí amatéri podradní profesionálom!

Najstaršie dôkazy Pytagorovej vety, ktoré sa k nám dostali, sú asi 2300 rokov staré. Jeden z nich - prísny axiomatický - patrí starogréckemu matematikovi Euklidovi, ktorý žil v 4. - 3. storočí pred n. e. V knihe I prvkov je Pytagorova veta uvedená ako návrh 47. Najgrafickejšie a najkrajšie dôkazy vychádzajú z pretvorenia „Pytagorových nohavíc“. Vyzerajú ako zložitá hádanka na rezanie štvorcov. Nechajte však kúsky pohybovať sa správne - a odhalia vám tajomstvo slávnej vety.

Tu je elegantný dôkaz získaný na základe kresby z jedného starodávneho čínskeho pojednania (obr. 3) a okamžite sa ukáže jeho súvislosť s problémom zdvojnásobenia plochy štvorca.

Práve tento dôkaz sa pokúsil vysvetliť svojmu mladšiemu priateľovi sedemročný Guido, predčasný hrdina poviedky „Malý Archimedes“ anglického spisovateľa Aldousa Huxleyho. Je kuriózne, že rozprávač, ktorý sledoval tento obraz, zaznamenal jednoduchosť a presvedčivosť dôkazu, a tak ho pripísal ... samotnému Pythagorasovi. ale hlavná postava fantastický príbeh Evgenyho Veltistova „Elektronika - chlapec z kufra“ poznal 25 dôkazov Pytagorovej vety, vrátane tých, ktoré uviedol Euklid; pravda, omylom ho označil za najjednoduchší, hoci v skutočnosti zaberá v modernom vydaní „Elementov“ jeden a pol strany!

Prvý matematik

Pytagoras zo Samosu (570-495 pred n. L.), Ktorého meno je už dlho nerozlučne spojené s pozoruhodnou vetou, možno v istom zmysle nazvať prvým matematikom. Práve s ním matematika začína ako exaktná veda, kde akékoľvek nové poznatky nie sú výsledkom vizuálnych zobrazení a pravidiel odvodených zo skúseností, ale výsledkom logického uvažovania a záverov. To je jediný spôsob, ako raz a navždy zistiť pravdivosť akýchkoľvek matematických tvrdení. Pred Pytagorasom sa využívala iba deduktívna metóda starogrécky filozof a vedec Thales z Milétu, ktorý žil na prelome 7. - 6. storočia pred n. e. Vyslovil samotnú myšlienku dôkazu, ale neaplikoval ju systematicky, selektívne, spravidla na zjavné geometrické výroky, ako napríklad „priemer rozdeľuje kruh na polovicu“. Pytagoras zašiel oveľa ďalej. Predpokladá sa, že predstavil prvé definície, axiómy a metódy dokazovania a taktiež vytvoril prvý kurz geometrie, ktorý starí Gréci poznali pod menom „Tradícia Pytagorova“. Stál tiež pri počiatkoch teórie čísel a stereometrie.

Ďalšou dôležitou zásluhou Pytagoriády je založenie slávnej školy matematikov, ktorá na viac ako storočie určovala vývoj tejto vedy v starovekom Grécku. S jeho menom sa spája aj výraz „matematika“ (z gréckeho slova μαθημa - náuka, veda), ktorý kombinuje štyri príbuzné disciplíny znalostného systému, ktoré vytvoril Pytagoras a jeho prívrženci - Pytagorejci - geometria, aritmetika, astronómia a harmonické.

Nie je možné oddeliť úspechy Pythagora od úspechov jeho študentov: podľa zvyku pripisovali svoje vlastné nápady a objavy svojmu učiteľovi. Ranní Pytagorejci nezanechali žiadne skladby, všetky informácie si navzájom odovzdávali ústne. Takže o 2 500 rokov neskôr historikom nezostáva nič iné, len zrekonštruovať stratené poznatky z prepisov iných, neskorších autorov. Poďme vzdať hold Grékom: hoci meno Pytagoras obklopili mnohými legendami, nepripisovali mu nič, čo by nemohol objaviť alebo z neho vyvinúť teóriu. A veta, ktorá nesie jeho meno, nie je výnimkou.

Taký jednoduchý dôkaz

Nie je známe, či sám Pythagoras objavil vzťah medzi dĺžkami strán v pravom trojuholníku, alebo si tieto poznatky požičal. Starí autori tvrdili, že on sám, a rád prerozprával legendu o tom, ako na počesť svojho objavu Pytagoras obetoval býka. Moderní historici majú tendenciu myslieť si, že o tejto vete sa dozvedel oboznámením sa s matematikou Babylončanov. Tiež nevieme, v akej podobe formuloval Pytagoros vetu: aritmeticky, ako je to dnes zvykom, - štvorec prepony sa rovná súčtu štvorcov nôh alebo geometricky v duchu staroveku, - štvorec postavený na preponu pravouhlého trojuholníka sa rovná súčtu štvorcov postavených na jeho nohy.

Predpokladá sa, že to bol Pytagoras, kto dal prvý dôkaz o vete, ktorá nesie jeho meno. Samozrejme to neprežilo. Podľa jednej z verzií mohol Pythagoras využiť doktrínu proporcií vyvinutú v jeho škole. Na ňom bola založená najmä teória podobnosti, na ktorej je založená úvaha. Nakreslite pravouhlý trojuholník s nohami a a b vo výške po preponu c. Získame tri podobné trojuholníky, vrátane pôvodného. Ich príslušné strany sú proporcionálne, a: c \u003d m: a a b: c \u003d n: b, odkiaľ a 2 \u003d c m a b 2 \u003d c n. Potom a 2 + b 2 \u003d \u003d c · (m + n) \u003d c 2 (obr. 4).

Toto je iba rekonštrukcia, ktorú navrhol jeden z historikov vedy, ale dôkaz, ako vidíte, je celkom jednoduchý: trvá len pár riadkov, nemusíte nič dokončovať, prekresľovať, počítať ... Niet divu, že bola znovuobjavená viackrát. Je obsiahnutá napríklad v „Cvičení z geometrie“ od Leonarda z Pisy (1220) a stále je citovaná v učebniciach.

Tento dôkaz nebol v rozpore s predstavami Pytagorovcov o porovnateľnosti: spočiatku sa domnievali, že pomer dĺžok akýchkoľvek dvoch segmentov, a teda oblasti plochých útvarov, možno vyjadriť pomocou prirodzených čísel. O ďalších číslach neuvažovali, nepovolili ani zlomky, nahradili ich pomermi 1: 2, 2: 3 atď. Je však ironické, že až Pytagorova veta priviedla Pytagorejčanov k zisteniu nesúmerateľnosti uhlopriečky štvorca a jeho strany. Všetky pokusy o numerické znázornenie dĺžky tejto uhlopriečky - pre jednotkový štvorec sa rovná √2 - nikam neviedli. Ľahšie sa ukázalo, že problém je neriešiteľný. V takom prípade majú matematici osvedčenú metódu dokázania rozporom. Mimochodom, pripisujú sa mu aj Pytagoras.

Existencia vzťahu, ktorý nie je vyjadrený prirodzeným počtom, ukončila mnohé pytagorejské myšlienky. Ukázalo sa, že čísla, ktoré poznali, nestačia na vyriešenie ani jednoduchých problémov, nehovoriac o celej geometrii! Tento objav bol zlomom vo vývoji gréckej matematiky, jej ústrednom probléme. Spočiatku to viedlo k rozvoju doktríny nekombinovateľných množstiev - iracionalít, a potom - k rozšíreniu koncepcie čísla. Inými slovami, začala sa ním stáročná história výskumu množiny reálnych čísel.

Pytagorova mozaika

Ak zakryjete lietadlo štvorcami dvoch rôznych veľkostí a každý malý štvorec obklopíte štyrmi veľkými, získate parketu „mozaika Pythagoras“. Takýto vzor dlho zdobil kamenné podlahy a pripomína starodávne dôkazy Pytagorovej vety (odtiaľ pochádza aj jej názov). Použitím štvorcovej mriežky na parkety rôznymi spôsobmi môžete získať priečky štvorcov postavené po stranách pravouhlého trojuholníka, ktoré navrhli rôzni matematici. Napríklad ak usporiadate mriežku tak, aby sa všetky jej uzly zhodovali s pravými hornými vrcholmi malých štvorcov, objavia sa fragmenty kresby ako dôkaz stredovekého perzského matematika al-Nayriziho, ktorý vložil do komentárov k Euklidovým začiatkom. Je ľahké vidieť, že súčet plôch veľkého a malého štvorca, pôvodných prvkov parkiet, sa rovná ploche jedného štvorca na ňom položenej mriežky. A to znamená, že určené rozdelenie je skutočne vhodné na pokládku parkiet: spojením výsledných mnohouholníkov do štvorcov, ako je znázornené na obrázku, môžete nimi vyplniť celú rovinu bez medzier a presahov.

Pytagorovu vetu pozná každý už od školských čias. Významný matematik dokázal veľkú hypotézu, ktorú dnes používa veľa ľudí. Pravidlo znie takto: štvorec dĺžky prepony pravouhlého trojuholníka sa rovná súčtu štvorcov nôh. Po mnoho desaťročí nebol žiadny matematik schopný argumentovať týmto pravidlom. Pytagoras napokon išiel dlho k svojmu cieľu, aby sa vo výsledku uskutočňovali kresby v každodennom živote.

1. Krátky verš k tejto vete, ktorý bol vynájdený krátko po dôkaze, priamo dokazuje vlastnosti hypotézy: „Pythagorove nohavice sú si vo všetkých smeroch rovnaké.“ Táto dvojriadka utkvela v pamäti mnohých ľudí - dodnes si báseň pamätajú výpočty.
2. Táto veta sa nazývala „Pytagorove nohavice“ vzhľadom na to, že pri kreslení v strede sa získal pravouhlý trojuholník, na stranách ktorého boli štvorce. Vzhľadovo táto kresba pripomínala nohavice - odtiaľ pochádza aj názov hypotézy.
3. Pythagoras bol hrdý na vyvinutú vetu, pretože táto hypotéza sa líši od podobných v maximálnom množstve dôkazov. Dôležité: Rovnica bola zapísaná do Guinnessovej knihy rekordov kvôli 370 pravdivým dôkazom.
4. Hypotézu mnohými spôsobmi dokázal obrovský počet matematikov a profesorov z rôznych krajín.... Anglický matematik Jones čoskoro oznámil, že hypotéza to dokázala pomocou diferenciálnej rovnice.
5. V súčasnosti nikto nevie dôkaz vety, ktorý predložil sám Pythagoras... Fakty o dôkazoch matematikov dnes nie sú známe nikomu. Predpokladá sa, že dôkaz kresieb od Euklida je dôkazom Pytagorasa. Niektorí vedci však argumentujú týmto tvrdením: mnohí sa domnievajú, že Euclid nezávisle dokázal teorém bez pomoci tvorcu hypotézy.
6. Dnešní vedci zistili, že veľký matematik túto hypotézu neobjavil ako prvý.... Rovnica bola známa dávno pred objavením Pytagoriády. Tento matematik dokázal iba znovu spojiť hypotézu.
7. Pythagoras nepomenoval rovnicu „Pythagorova veta“... Toto meno uviazlo po „hlasnej dvojriadke“. Matematik iba chcel, aby jeho úsilie a objavy uznal a využil celý svet.
8. Moritz Cantor - vynikajúci vynikajúci matematik, ktorý sa našiel a rozoznal v záznamoch o starom papyruse pomocou kresieb... Krátko nato si Cantor uvedomil, že túto vetu poznali Egypťania už v roku 2300 pred naším letopočtom. Len potom to nikto nepoužil a neskúšal to dokázať.
9. Súčasní vedci sa domnievajú, že hypotéza bola známa už v 8. storočí pred naším letopočtom... Vtedajší indickí vedci objavili približný výpočet prepony trojuholníka obdareného pravými uhlami. Je pravda, že v tom čase nebol nikto schopný s istotou dokázať rovnicu hrubými výpočtami.
10. Veľký matematik Bartel van der Waerden po preukázaní hypotézy uzavrel dôležitý záver: „Za zásluhy gréckeho matematika sa nepovažuje objav smeru a geometrie, ale iba jeho opodstatnenie. V rukách Pythagora boli výpočtové vzorce, ktoré boli založené na predpokladoch, nepresných výpočtoch a neurčitých predstavách. Vynikajúcemu vedcovi sa to však podarilo zmeniť na exaktnú vedu. ““
11. Slávny básnik povedal, že v deň otvorenia svojej kresby postavil býkom slávnu obetu... Bolo to po objavení hypotézy, že sa rozšírili fámy, že obeta sto býkov „išla blúdiť po stránkach kníh a publikácií“. Dôvtip dodnes vtipkuje, že odvtedy sa všetci býci obávajú nového objavu.
12. Dôkaz, že Pytagoras neprišiel s básňou o nohaviciach, aby dokázal svoje kresby: počas života veľkého matematika neboli nohavice... Boli vynájdené o niekoľko desaťročí neskôr.
13. Pekka, Leibniz a niekoľko ďalších vedcov sa pokúsili dokázať predtým známu vetu, ale nikto neuspel.
14. Názov kresby „Pytagorova veta“ znamená „presvedčenie rečou“... Takto sa prekladá slovo Pythagoras, ktoré matematik vzal ako pseudonym.
15. Úvahy Pytagorasa o jeho vlastnej vláde: tajomstvo existencie na zemi spočíva v počte... Napokon, matematik, spoliehajúc sa na svoju vlastnú hypotézu, študoval vlastnosti čísel, odhalil párnosť a nepárnosť a vytvoril proporcie.

Dúfame, že sa vám výber s obrázkami páčil - Zaujímavosti o Pytagorovej vete: dozvedáme sa nové veci o slávnej vete (15 fotografií) v dobrej kvalite. Váš názor nechajte prosím v komentároch! Každý názor je pre nás dôležitý.