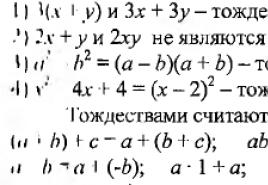Ako previesť výraz na identicky rovný. Identické premeny výrazov, ich typy

Identické premeny

1. Pojem identity. Hlavné typy identických transformácií a štádiá ich štúdia.

11 učenie sa rôznych transformácií výrazov a vzorcov zaberá v školskom kurze matematiky slabú časť študijného času. Najjednoduchšie ^ "" vzdelávanie, založené na vlastnostiach aritmetických operácií, je už na základnej škole. Ale hlavnú záťaž na formovanie zručností a schopností vykonávať transformácie nesie kurz školskej algebry 1> potom je spojený:

s prudkým nárastom počtu vykonávaných transformácií, ich variabilita;

s komplikáciou činností ich zdôvodniť a objasniť podmienky použiteľnosti;

i) s izoláciou a štúdiom zovšeobecnených pojmov identity, identickej transformácie, ekvivalentnej transformácie, logického dôsledku.

Línia identických transformácií sa v kurze algebry na základnej škole rozvíja takto:

, 4 b triedy - otváranie zátvoriek, prinášajúce podobné výrazy, odober- M (Chsho faktor mimo zátvoriek;

7 Trieda - identické transformácie celočíselných a zlomkových výrazov;

Trieda H - identické transformácie výrazov obsahujúcich odmocniny;

( > trieda - identické transformácie goniometrických výrazov a mmrizhsny, obsahujúce stupeň s racionálnym exponentom.

Línia identických transformácií je jednou z dôležitých ideologických línií kurzu algebry. Preto je vyučovanie matematiky v 5. – 6. ročníku postavené tak, aby žiaci už v týchto ročníkoch získali zručnosti najjednoduchších identických transformácií (bez použitia pojmu „identické premeny“). Tieto zručnosti sa formujú pri vykonávaní cvičenia na uvádzanie podobných výrazov, otváranie zátvoriek a zátvoriek, vyberanie faktora zo zátvoriek atď. Do úvahy sa berú aj najjednoduchšie prevody číselných a doslovných výrazov. Na tejto úrovni učenia sa ovládajú transformácie, ktoré sa vykonávajú priamo na základe zákonitostí a vlastností počtových operácií.

Medzi hlavné typy úloh v ročníkoch 5-6, pri riešení ktorých sa aktívne využívajú vlastnosti a zákony aritmetických operácií a prostredníctvom ktorých sa formujú zručnosti identických transformácií, patria:

zdôvodnenie algoritmov na vykonávanie akcií na číslach študovaných číselných súborov;

výpočet hodnôt číselného výrazu najracionálnejším spôsobom;

porovnanie hodnôt číselných výrazov bez vykonania zadaných akcií;

zjednodušenie doslovných výrazov;

dôkaz o rovnosti hodnôt dvoch písmenových výrazov atď.

Uveďte číslo 153 ako súčet ciferných členov; ako rozdiel dvoch čísel, ako súčin dvoch čísel.

Predstavte si číslo 27 ako súčin troch rovnakých faktorov.

Tieto cvičenia na znázornenie toho istého čísla v rôznych formách zápisu prispievajú k asimilácii konceptu identických transformácií. Spočiatku môžu byť tieto reprezentácie ľubovoľné, neskôr - účelové. Napríklad zobrazenie vo forme súčtu ciferných pojmov sa používa na vysvetlenie pravidiel pre sčítanie prirodzených čísel "v stĺpci", zobrazenie vo forme súčtu alebo rozdielu "vhodných" čísel - na vykonávanie rýchlych výpočtov rôznych produkty, reprezentácia vo forme súčinu faktorov – na zjednodušenie rôznych zlomkových výrazov.

Nájdite význam výrazu 928 36 + 72 36.

Racionálny spôsob výpočtu hodnoty tohto výrazu je založený na použití distribučného zákona násobenia vzhľadom na sčítanie: 928 36 + 72 36 = (928 + 72) 36 = 1000 36 = 36000.

V školskom kurze matematiky možno rozlíšiť nasledujúce stupne zvládnutia aplikácií transformácií alfanumerických výrazov a vzorcov.

etapa. Začiatky algebry. V tomto štádiu sa používa nedelený systém transformácií; reprezentujú ho pravidlá vykonávania akcií na jednej alebo oboch častiach vzorca.

Príklad. Riešte rovnice:

a) 5x - bx = 2; b) 5x = 3x + 2; v) 6 (2 - 4 roky) + 5r = 3 (1 - Zu).

Všeobecnou myšlienkou riešenia je zjednodušiť tieto vzorce pomocou niekoľkých pravidiel. V prvej úlohe zjednodušenie sa dosiahne použitím identity: 5x- Bx= (5 - 3) x. Transformácia identity založená na tejto identite transformuje danú rovnicu na ekvivalentnú ursómiu 2x - 2.

Druhá rovnica vyžaduje na svoje riešenie nielen identickú, ale skutočnú transformáciu; v tejto funkcii sa tu používa pra- || n prenesením členov rovnice z jednej časti rovnice do druhej so zmeneným šik. Pri riešení už tak jednoduchej úlohy ako je b) sa použijú oba mon v transformáciách - identické aj ekvivalentné. Toto ustanovenie platí aj pre ťažkopádnejšie úlohy, ako je napríklad tretia.

Krtkom prvej fázy je naučiť, ako rýchlo riešiť najjednoduchšie rovnice, zjednodušiť vzorce, ktoré definujú funkcie, racionálne vykonávať výpočty založené na vlastnostiach akcií.

sýkorka. Formovanie zručností pri aplikácii špecifických typov transformáciíII nakloniť Pojmy identity a identickej transformácie sú explicitne zavedené v kurze shn "sbry 7. ročník. Takže napríklad v učebnici Yu. N. Makarycheva" Algebra 7 "nnp" shle je zavedený pojem identicky rovnocenných výrazov: "Dva výrazy, ktorých zodpovedajúce hodnoty sú rovnaké pre všetky premenné hodnôt, sa posypú." identicky rovnaké ", potom koncept identity: „Nazýva sa rovnosť spárovaná pre akékoľvek hodnoty premenných identita“.

11 uvádza príklady:

V učebnici A.G. Mordkovichova „Algebra 7“ okamžite poskytuje rafinovaný koncept identity: „Identita je rovnosť pravdivá za akékoľvek prípustné hodnoty jeho základných premenných “.

Pri zavádzaní konceptu identických transformácií by sme sa mali v prvom rade zbaviť vhodnosti štúdia identických transformácií. Na tento účel môžete zvážiť rôzne cvičenia na nájdenie významu výrazov.

liiiipiiMep, nájdite hodnotu výrazu 37,1x + 37, ly s X= 0,98, y = 0,02. Použitím distribučnej vlastnosti násobenia výraz 37,1l + 37,1 pri možno vyjadriť výrazom 37,1 (x + y), jemu identicky rovný. Ešte pôsobivejšie riešenie červa 1 k nasledujúcemu cvičeniu: nájdite význam výrazu

() - (a-6) _ n p i. a) d = h>^ = 2; b) a = 121, B - 38; c) a = 2,52, B = 1 -.

ab 9

11po vykonaných transformáciách sa ukazuje, že množina hodnôt tohto odrazu pozostáva z jedného čísla 4.

V učebnici „Algebra 7“ od Yu. N. Makarycheva je zavedenie pojmu identickej transformácie motivované uvažovaním príkladu: „Nájsť význam výrazu xy – áno v x = 2,3; y = 0,8; z = 0,2, musíte vykonať 3 akcie: hu - xz = 2,3 0,8 - 2,3 0,2 = 1,84 - 0,46 = 1,38.

11 je potrebné poznamenať jeden typ transformácií špecifický pre priebeh algebry a začiatky analýzy. Ide o transformácie výrazov obsahujúcich prechody, a transformácie založené na pravidlách diferenciácie a integrácie. Hlavný rozdiel medzi týmito „analytickými“ transformáciami od „algebraických“ transformácií je v charaktere množiny, ktorá prechádza premennými v identitách. V algebraických identitách premenné prebiehajú číselné oblasti, a v analytických súboroch tieto súbory ■ ostávajú isté veľa funkcií. Napríklad pravidlo diferenciálneho súčtu: (Z "+ g)" tu / a g sú premenné prechádzajúce množinou

I I ale diferencovateľné funkcie so spoločnou doménou definície. Navonok sú tieto transformácie podobné transformáciám algebraického typu, preto sa niekedy hovorí „algebra limit“, „algebra diferenciácie“.

Identity študované v školskom kurze algebry a algebraickom ma-riáli kurzu algebry a princípoch analýzy možno rozdeliť na dve triedy.

Prvý pozostáva zo skrátených multiplikačných identít, spravodlivý v

av.

iiioGom komutatívny kruh a identity sú = -, a * 0, ktorá platí v ľubovoľnom

Oom pole.

Druhú triedu tvoria identity spájajúce aritmetické čísla a základné elementárne funkcie, ako aj kompozície elementárnychHhixfunkcie. Väčšina identít tejto triedy má tiež spoločný matematický základ, ktorým je, že exponenciálne, exponenciálne a logaritmické funkcie sú izomorfizmy rôznych číselných skupín. Napríklad platí nasledovné tvrdenie: existuje jedinečné spojité izomorfné zobrazenie / aditívnej skupiny reálnych čísel do multiplikatívnej skupiny kladných reálnych čísel, v ktorom je jednotka zobrazená na dané číslo. a> 0, a f 1; toto zobrazenie je dané inkrementálnou funkciou s radixom a:/(X)= a. Pre mocninné a logaritmické funkcie existujú podobné výroky.

Metodológia štúdia identít v oboch triedach má mnoho spoločných čŕt. Vo všeobecnosti medzi identické transformácie študované v kurze školskej matematiky patria:

transformácie výrazov obsahujúcich radikály a mocniny so zlomkovými exponentmi;

transformácie výrazov obsahujúcich limitné prechody a transformácie založené na pravidlách diferenciácie a integrácie.

Tento výsledok možno dosiahnuť vykonaním iba dvoch krokov - ak použijete výraz x (y-z), identicky sa rovná výrazu xy-xz: x (y-Z) = 2,3 (0,8 - 0,2) = 2,3 0,6 = 1,38.

Výpočty sme zjednodušili nahradením výrazu xy-xz identicky rovnaký výraz x (y - z).

Nahradenie jedného výrazu iným, identicky sa mu rovným, sa nazýva identická transformácia alebo jednoducho transformáciou výrazu“.

Zvládnutie rôznych typov transformácií v tejto fáze začína zavedením skrátených vzorcov násobenia. Potom uvažujeme o transformáciách spojených s operáciou umocňovania s rôznymi triedami elementárnych funkcií - exponenciálna, exponenciálna, logaritmická, trigonometrická. Každý z týchto typov premien prechádza štádiom štúdia, v ktorom sa pozornosť sústreďuje na asimiláciu ich charakteristických čŕt.

Ako sa materiál hromadí, je možné vyčleniť a na tomto základe zaviesť koncepty identických a ekvivalentných transformácií.

Treba poznamenať, že pojem identická transformácia sa v kurze školskej algebry neuvádza v úplnej všeobecnosti, ale iba v aplikácii na výrazy. Transformácie sú rozdelené do dvoch tried: identické premeny sú transformácie výrazov, a ekvivalent - konvertovanie vzorcov. V prípade, že je potrebné zjednodušiť jednu časť vzorca, je v tomto vzorci zvýraznený výraz, ktorý slúži ako argument pre použitú identickú transformáciu. Napríklad rovnice 5x - Zx - 2 a 2x = 2 sa považujú nielen za rovnocenné, ale za rovnaké.

V učebniciach algebry Sh.A. Alimova et al., Pojem identita nie je explicitne zavedený v 7. – 8. ročníku a až v 9. ročníku v téme „Trigonometrické identity“ pri riešení úlohy 1: „Dokážte, že za afkk, Komu < eZ , platí rovnosť 1 + ctg 2 a = - \ -, tento pojem sa zavádza. Tu je žiakom vysvetlené, že hrešia a

uvedená rovnosť „platí pre všetky prípustné hodnoty a, t.j. tak, aby jeho ľavá a pravá strana dávala zmysel. Takéto rovnoprávnosti sa nazývajú identity, a problémy dokazovania takejto rovnosti sa nazývajú problémy dokazovania totožnosti."

Stupeň III. Organizácia integrálneho systému transformácií (syntéza).

Hlavným cieľom tejto etapy je vytvorenie flexibilného a výkonného aparátu vhodného na použitie pri riešení rôznych vzdelávacích úloh.

K nasadeniu druhého stupňa štúdia transformácií dochádza počas celého kurzu algebry základnej školy. Prechod do tretej etapy sa uskutočňuje záverečným opakovaním kurzu v rámci pochopenia už známeho učiva, po častiach, pre jednotlivé typy transformácií.

V priebehu algebry a začiatkov analýzy sa v podstate už vytvorený integrálny systém transformácií postupne zdokonaľuje. Pridávajú sa k nemu aj niektoré nové typy transformácií (napríklad súvisiace s goniometrickými a logaritmickými funkciami), ktoré ho však len obohacujú, rozširujú jeho možnosti, ale nemenia jeho štruktúru.

Metodológia štúdia týchto nových transformácií sa prakticky nelíši od metodiky používanej v kurze algebry.

Je potrebné poznamenať jeden typ transformácií, špecifický pre Kurenovu algebru a začiatky analýzy. Ide o transformácie výrazov obsahujúcich obmedziť prechody, a transformácie založené na pravidlách diferenciácie a integrácie. Hlavný rozdiel medzi týmito „analytickými“ transformáciami a „algebraickými“ transformáciami je v povahe množiny, ktorou premenné prechádzajú v identitách. V algebraických identitách premenné prebiehajú číselné oblasti, a v analytickej oblasti tieto súpravy žiaria s istotou veľa funkcií. Napríklad pravidlo na rozlíšenie sumy: ( f + g )" = f + g "; tu fug - premenné prechádzajúce viacerými diferencovateľnými funkciami so spoločnou doménou definície. Navonok sú tieto transformácie podobné transformáciám algebraického typu, preto sa niekedy hovorí „algebra limit“, „algebra diferenciácie“.

Identity študované v školskom kurze algebry a algebraický materiál kurzu algebry a princípy analýzy možno rozdeliť na dve triedy.

Prvý pozostáva zo skrátených multiplikačných identít, spravodlivý v

ľubovoľný komutatívny kruh a identita - = -, a * 0, platná v ľubovoľnom

eso s

Druhú triedu tvoria identity spájajúce aritmetické operácie a základné elementárne funkcie, ako aj kompozície elementárnych funkcií. Väčšina identít tejto triedy má tiež spoločný matematický základ, ktorým je, že mocninné, exponenciálne a logaritmické funkcie sú izomorfizmy rôznych číselných skupín. Napríklad platí nasledovné tvrdenie: existuje jedinečné spojité izomorfné zobrazenie / aditívnej skupiny reálnych čísel na multiplikatívnu skupinu kladných reálnych čísel, v ktorej je jednotka zobrazená na dané číslo. a> 0, a f jeden; toto zobrazenie je dané exponenciálnou funkciou s radix i: / (x) = a *. Pre mocninné a logaritmické funkcie existujú podobné výroky.

Metodológia štúdia identít oboch tried má mnoho spoločných čŕt. Vo všeobecnosti medzi identické transformácie študované v kurze školskej matematiky patria:

transformácie algebraických výrazov;

prevod výrazov obsahujúcich radikály a mocniny na zlomkové exponenty;

prevod goniometrických výrazov;

prevod výrazov obsahujúcich stupne a logaritmy;

transformácie výrazov obsahujúcich limitné prechody a transformácie založené na pravidlách, diferenciácii a integrácii.

2. Vlastnosti organizácie systému úloh pri štúdiu identických transformácií

Základným princípom organizovania akéhokoľvek systému úloh je ich prezentácia od jednoduchých po zložité berúc do úvahy potrebu žiakov prekonávať realizovateľné ťažkosti a vytvárať problémové situácie. Tento základný princíp si vyžaduje konkretizáciu vo vzťahu k osobitostiam tohto vzdelávacieho materiálu. Tu je príklad systému cvičení na tému: „Druhá mocnina súčtu a

rozdiel dvoch čísel“.

I la tento základný cvičebný systém končí. Takýto systém by mal zabezpečiť asimiláciu základného materiálu.

Nasledujúce cvičenia (17-19) umožňujú žiakom zamerať sa na bežné chyby a prispieť k rozvoju záujmu a ich tvorivých 1 pomôcok.

V každom konkrétnom prípade môže byť počet cvičení v systéme menší alebo väčší, ale postupnosť ich vykonávania by mala byť rovnaká.

Popísať rôzne sústavy úloh v metodológii matematiky, pojem o cvičebný cyklus. Cyklus cvičení je charakteristický tým, že viaceré aspekty štúdia a techniky usporiadania látky sú prepojené v slede cvičení. Pokiaľ ide o identické transformácie, koncept cyklu možno uviesť nasledovne.

11. cyklus cvičení je spojený so štúdiom jednej identity, okolo ktorej sa zoskupujú ďalšie identity, ktoré sú s ňou v prirodzenom spojení. V „zastavení cyklu spolu s výkonný zahŕňa úlohy vyžadujúce spoznávanie< ii v ani použiteľnosť posudzovanej identity. Študovaná identita sa používa na vykonávanie výpočtov v rôznych číselných oblastiach.

Úlohy v každom cykle sú rozdelené na dve skupiny. TO prvý zahŕňa úlohy vykonávané pri prvotnom oboznámení sa s identitou. Vykonávajú sa v niekoľkých vyučovacích hodinách, ktoré spája jedna téma. Druhá skupina cvičenia spája študovanú identitu s rôznymi aplikáciami. Cvičenia v tejto skupine sú zvyčajne roztrúsené na rôzne témy.

Opísaná štruktúra cyklu sa vzťahuje na štádium formovania zručností pri uplatňovaní konkrétnych typov transformácií. V záverečnej fáze - (Tanya syntéza, cykly sú modifikované. po prvé, obe skupiny shdapiy sa kombinujú, tvoria sa Rozvinutý cyklus , a z prvej skupiny sú vylúčené tie najjednoduchšie z hľadiska znenia či náročnosti vyhotovenia záznamu. Zostávajúce typy úloh sú komplikovanejšie. po druhé, dochádza k zlúčeniu cyklov súvisiacich s rôznymi identitami, vďaka čomu sa zvyšuje úloha akcií pri rozpoznávaní použiteľnosti jednej alebo druhej identity.

11RNNSUveďme konkrétny príklad slučky.

Príklad. Cyklus úloh pre identitu x -y 2 = (x-y) (x + y).

Vykonávanie prvej skupiny úloh tohto cyklu prebieha takto -

podmienky. Študenti sa práve zoznámili s formuláciou identity (resp. s dvomi formuláciami: „Rozdiel druhých mocnín dvoch výrazov sa rovná súčinu súčtu a rozdielu týchto výrazov“ a „Súčin súčet a rozdiel dvoch výrazov sa rovná rozdielu druhých mocnín týchto výrazov"), napíšte ho vo forme vzorca, dôkazu ... Potom je tu niekoľko príkladov, ako použiť transformáciu založenú na tejto identite. Nakoniec študenti začnú robiť cvičenia sami.

Prvá skupina úloh

Druhá skupina úloh

(Úlohy každej skupiny môžu byť prezentované študentom pomocou multimediálneho projektora)

Urobme metodologickú analýzu tohto systému typov úloh.

Úloha a0 je určená na upevnenie štruktúry skúmanej identity. To sa dosiahne nahradením písmen (x a y) v zápise totožnosti v iných listoch. Úlohy tohto typu umožňujú objasniť vzťah medzi verbálnym prejavom a symbolickou formou identity.

Úloha a 2) je zameraná na vytvorenie spojenia medzi touto identitou a číselným systémom. Výraz, ktorý sa má previesť, tu nie je čisto doslovný, ale alfanumerický. Na popis vykonaných akcií je potrebné použiť koncept substitúciečíslo písmen v identite. Rozvoj zručností

uplatnenie substitučnej operácie a prehĺbenie jej porozumenia vykonávané I um pri plnení úloh typu d 2).

Ďalší krok pri osvojovaní identity ilustruje úloha a). V mennom priradení výraz navrhnutý na transformáciu nemá tvar rašplových n štvorcov; transformácia je možná len vtedy. h (chp1k si všimne, že číslo 121 možno znázorniť ako druhú mocninu čísla. Táto úloha sa teda nevykoná v jednom kroku, ale v dvoch: na prvomiiiiu existuje uznanie možnosti zredukovať tento výraz na MPD rozdielu štvorcov, na druhom pomocou identity sa vykoná transformácia.

Na začiatku vývoja identity sa zaznamenáva každý krok:

I "I / s 2 = 11 2 - & 2 = (11 - £) (11 + do), neskôr niektoré rozpoznávacie operácie žiaci vykonávajú ústne.

V príklade dd) je potrebné vytvoriť spojenie medzi touto identitou a ostatnými súvisiacimi s akciami s monomími; v q 3) treba použiť identitu pre rozdiel štvorcov dvakrát; c) študenti budú musieť prekonať určitú psychologickú bariéru a dostať sa do oblasti iracionálnych čísel.

Úlohy typu b) sú zamerané na rozvoj zručností pri výmene produktu (, v - y) (x + y) rozdielom X 2 - pri 2 . Podobnú úlohu zohrávajú úlohy typu c). V príkladoch typu d) je potrebné zvoliť jeden zo smerov transformácie.

Vo všeobecnosti sú úlohy prvej skupiny zamerané na zvládnutie štruktúry identity, substitučných operácií v najjednoduchších najdôležitejších prípadoch a predstavy o reverzibilite transformácií uskutočňovaných identitou,

Hlavné črty a ciele, ktoré sme zverejnili pri zvažovaní prvého | ruiny cyklov priradenia, odkazujú na akýkoľvek cyklus cvičenia, ktorý tvorí bodáky používania identity. Pre každú novo zavedenú identitu si prvá skupina úloh v cykle musí zachovať tu opísané vlastnosti; rozdiely môžu byť len v počte úloh.

1 Druhá skupina úloh v cykle je na rozdiel od prvej zameraná na čo najplnšie využitie a zohľadnenie špecifík tejto konkrétnej identity, t i pi. Úlohy tejto skupiny predpokladajú už vytvorené zručnosti používať identitu pre rozdiel štvorcov (v najjednoduchších prípadoch); chi, úlohou tejto skupiny je prehĺbiť pochopenie identity zvažovaním jej rôznych aplikácií v rôznych situáciách v kombinácii s použitím materiálu súvisiaceho s inými témami kurzu matematiky.

Zvážte riešenie úlohy l):

x 3 - 4x = 15 o x 3 - 9x = 15 - 5x o x (x ~ 3) (x + 3) = 5 (3-x) x = 3, alebo \{\ 1-3) = -5. Rovnica x (x + 3) = -5 teda nemá skutočné korene \ 3 je jediný koreň rovnice.

Vidíme, že použitie identity pre rozdiel štvorcov je časť pn a I v riešení príkladu, čo je hlavná myšlienka vykonávania transformácií.

Cykly úloh spojených s identitami pre elementárne funkcie majú svoje vlastné charakteristiky, ktoré sú spôsobené tým, že na prvom mieste... zodpovedajúce identity sa skúmajú v súvislosti so štúdiom funkčného materiálu a, / u> - "toykh, objavujú sa neskôr ako identity prvej skupiny a študujú sa s

pomocou už vytvorených zručností vykonávania identických transformácií. Významná časť využitia identických transformácií spojených s elementárnymi funkciami pripadá na riešenie iracionálnych a transcendentálnych rovníc. Cykly súvisiace s asimiláciou identít zahŕňajú len tie najjednoduchšie rovnice, ale už tu je vhodné popracovať na zvládnutí techniky riešenia takýchto rovníc: redukciu nahradením neznámej rovnicou algebraickou.

Postupnosť krokov pre toto riešenie je nasledovná:

a) nájdite funkciu<р, для которой данное уравнение/(х) = 0 представимо в виде F (ср(лг)) = 0;

b) vykonať náhradu pri= cp (x) a vyriešte rovnicu F (y) = 0;

c) vyriešte každú z rovníc <р(х) = kde (at j) je množina koreňov rovnice F (y) = 0.

Novou otázkou, ktorú treba brať do úvahy pri štúdiu identít s elementárnymi funkciami, je zváženie domény definície. Tu sú príklady troch úloh:

a) Nakreslite funkciu y = 4 log 2 x.

b) Vyriešte rovnicu lg X + lg (x - 3) = 1.

c) V akej množine je vzorec lg (x - 5) + lg (x + 5) = lg ( X 2 - 25) je identita?

Typickou chybou, ktorej sa žiaci pri riešení úlohy a) dopúšťajú, je používanie rovnosti a 1. vylučujúca podmienka B> 0. V tomto prípade sa v dôsledku toho ukáže, že požadovaný graf má tvar paraboly namiesto správnej odpovede - pravej vetvy paraboly. V úlohe b) je zobrazený jeden zo zdrojov na získanie zložitých sústav rovníc a nerovníc, kedy je potrebné brať do úvahy oblasti definície funkcií a v úlohe c) - cvičenie, ktoré môže slúžiť ako prípravné.

Myšlienka, ktorá spája tieto úlohy - potreba študovať oblasť definície funkcie, môže vyjsť na svetlo iba pri porovnávaní takýchto úloh, ktoré sú vo svojej vonkajšej podobe odlišné. Význam tejto myšlienky pre matematiku je veľmi veľký. Môže slúžiť ako základ pre niekoľko cyklov cvičení - pre každú z tried elementárnych funkcií.

Na záver poznamenávame, že štúdium identických premien v škole má veľký vzdelávaciu hodnotu. Schopnosť robiť nejaké výpočty, vykonávať výpočty, po dlhú dobu s neustálou pozornosťou sledovať nejaký objekt, je potrebná pre ľudí rôznych profesií, bez ohľadu na to, či pracujú v oblasti duševnej alebo fyzickej práce. Špecifickosť sekcie „Identické premeny výrazov“ je taká, že študentom otvára široké možnosti na rozvoj týchto dôležitých profesijne významných zručností.

Konverzie identity predstavujú prácu, ktorú robíme s číselnými a doslovnými výrazmi, ako aj s výrazmi, ktoré obsahujú premenné. Všetky tieto transformácie vykonávame, aby sme pôvodný výraz dostali do formy, ktorá bude vhodná na riešenie problému. V tejto téme zvážime hlavné typy identických transformácií.

Identická konverzia výrazu. Čo to je?

Prvýkrát sa stretávame s pojmom identické transformované, sme na hodinách algebry v 7. ročníku. Zároveň sa najprv oboznamujeme s pojmom zhodne rovnocenné výrazy. Poďme pochopiť pojmy a definície, aby bola téma ľahšie pochopiteľná.

Definícia 1

Identická konverzia výrazu- sú to úkony vykonávané s cieľom nahradiť pôvodný výraz výrazom, ktorý bude identicky rovnaký ako pôvodný.

Často sa táto definícia používa v skrátenej forme, v ktorej je vynechané slovo „identický“. Predpokladá sa, že v každom prípade transformáciu výrazu vykonáme tak, aby sme získali výraz zhodný s pôvodným, a to netreba zvlášť zdôrazňovať.

Ilustrujme túto definíciu na príkladoch.

Príklad 1

Ak nahradíme výraz x + 3 - 2 na identický výraz x + 1, potom vykonáme identickú transformáciu výrazu x + 3 - 2.

Príklad 2

Nahradenie výrazov 2 a 6 výrazom a 3 Je identická transformácia, pričom nahradenie výrazu X na vyjadrenie x 2 nie je identická transformácia, keďže výrazy X a x 2 nie sú identicky rovnaké.

Upozorňujeme na formu písania výrazov pri vykonávaní identických transformácií. Pôvodný výraz a výsledný výraz zvyčajne píšeme ako rovnosť. Takže písanie x + 1 + 2 = x + 3 znamená, že výraz x + 1 + 2 bol zredukovaný na tvar x + 3.

Postupné vykonávanie akcií nás vedie k reťazcu rovnosti, čo je niekoľko rovnakých transformácií umiestnených v rade. Označenie x + 1 + 2 = x + 3 = 3 + x teda chápeme ako postupné vykonanie dvoch transformácií: najprv sa výraz x + 1 + 2 preniesol do tvaru x + 3 a do tvar 3 + x.

Identické transformácie a ODU

Množstvo výrazov, ktoré sa začíname učiť v 8. ročníku, nedáva zmysel pre všetky hodnoty premenných. Vykonávanie identických transformácií v týchto prípadoch vyžaduje, aby sme venovali pozornosť rozsahu prípustných hodnôt premenných (ADV). Vykonávanie rovnakých transformácií môže ponechať ODZ nezmenenú alebo ju zúžiť.

Príklad 3

Pri skoku z výrazu a + (- b) k výrazu a - b variabilný rozsah a a b zostáva rovnaký.

Príklad 4

Prejdite od výrazu x k výrazu x 2 x vedie k zúženiu rozsahu prípustných hodnôt premennej x z množiny všetkých reálnych čísel na množinu všetkých reálnych čísel, z ktorých bola vylúčená nula.

Príklad 5

Identická konverzia výrazu x 2 x výraz x vedie k rozšíreniu rozsahu prípustných hodnôt premennej x z množiny všetkých reálnych čísel okrem nuly na množinu všetkých reálnych čísel.

Zúženie alebo rozšírenie rozsahu prípustných hodnôt premenných pri vykonávaní rovnakých transformácií je dôležité pri riešení problémov, pretože môže ovplyvniť presnosť výpočtov a viesť k chybám.

Základné premeny identity

Pozrime sa teraz, čo sú identické transformácie a ako sa vykonávajú. Do hlavnej skupiny vyčleňme tie typy identických transformácií, s ktorými sa najčastejšie stretávame.

Okrem základných identických transformácií existuje množstvo transformácií, ktoré sa týkajú výrazov konkrétneho typu. Pri zlomkoch ide o metódy redukcie a redukcie na nového menovateľa. Pre výrazy s odmocninami a mocninami sú to všetky akcie, ktoré sa vykonávajú na základe vlastností odmocnín a mocnin. Pre logaritmické výrazy, akcie, ktoré sa vykonávajú na základe vlastností logaritmov. Pre goniometrické výrazy všetky akcie využívajúce goniometrické vzorce. Všetky tieto súkromné ​​transformácie sú podrobne opísané v samostatných témach, ktoré nájdete v našom zdroji. V tomto ohľade sa im v tomto článku nebudeme venovať.

Prejdime k zváženiu hlavných identických transformácií.

Permutácia pojmov, faktory

Začnime preskupením pojmov. S touto identickou premenou sa stretávame najčastejšie. A za základné pravidlo tu možno považovať nasledovné tvrdenie: v akomkoľvek súčte permutácia pojmov na miestach neovplyvňuje výsledok.

Toto pravidlo je založené na posunových a kombinačných vlastnostiach sčítania. Tieto vlastnosti nám umožňujú preusporiadať termíny na miestach a získať tak výrazy, ktoré sú identicky rovnaké ako pôvodné. Preto je permutácia pojmov na miestach v súčte transformáciou identity.

Príklad 6

Máme súčet troch členov 3 + 5 + 7. Ak zameníme výrazy 3 a 5, výraz bude mať tvar 5 + 3 + 7. V tomto prípade existuje niekoľko možností, ako zmeniť usporiadanie podmienok. Všetky vedú k získaniu výrazov, ktoré sú identické s pôvodným.

Nielen čísla, ale aj výrazy môžu v súčte pôsobiť ako výrazy. Rovnako ako čísla môžu byť preusporiadané na miestach bez toho, aby to ovplyvnilo konečný výsledok výpočtov.

Príklad 7

V súčte troch členov 1 a + b, a 2 + 2 a + 5 + a 7 a 3 a - 12 a tvaru 1 a + b + a 2 + 2 a + 5 + a 7 a 3 + ( - 12) · výrazy možno preusporiadať napríklad takto (- 12) Na druhej strane môžete preusporiadať pojmy v menovateli zlomku 1 a + b a zlomok bude mať tvar 1 b + a. A výraz pod koreňovým znakom a 2 + 2 a + 5 je tiež suma, v ktorej je možné vymeniť podmienky.

Rovnako ako výrazy, v pôvodných výrazoch môžete zmeniť miesta faktorov a získať identicky správne rovnice. Táto akcia sa riadi nasledujúcim pravidlom:

Definícia 2

V produkte nemá preusporiadanie multiplikátorov na miestach vplyv na výsledok výpočtu.

Toto pravidlo je založené na posunovacích a kombinačných vlastnostiach násobenia, ktoré potvrdzujú správnosť identickej transformácie.

Príklad 8

Práca 3 5 7 permutácia faktorov môže byť reprezentovaná jednou z nasledujúcich foriem: 5 3 7, 5 7 3, 7 3 5, 7 5 3 alebo 3 7 5.

Príklad 9

Preusporiadanie faktorov v produkte x + 1 x 2 - x + 1 x dáva x 2 - x + 1 x x + 1

Rozširujúce zátvorky

Zátvorky môžu obsahovať číselné a variabilné výrazy. Tieto výrazy je možné previesť na identicky rovnaké výrazy, v ktorých nebudú žiadne zátvorky alebo ich bude menej ako v pôvodných výrazoch. Tento spôsob prevodu výrazov sa nazýva rozšírenie zátvoriek.

Príklad 10

Vykonajme akcie so zátvorkami vo vyjadrení formulára 3 + x - 1 x aby sme dostali identicky správny výraz 3 + x - 1 x.

Výraz 3 x - 1 + - 1 + x 1 - x možno previesť na zhodne rovnaký výraz bez zátvoriek 3 x - 3 - 1 + x 1 - x.

Podrobne sme opísali pravidlá prevodu výrazov so zátvorkami v téme "Rozširovanie zátvoriek", ktorá je uverejnená na našom zdroji.

Zoskupovanie pojmov, faktory

V prípadoch, keď máme do činenia s tromi alebo viacerými pojmami, môžeme siahnuť po takej forme identických transformácií, ako je zoskupovanie pojmov. Tento spôsob transformácií znamená spojenie niekoľkých pojmov do skupiny ich preusporiadaním a uzavretím do zátvoriek.

Pri zoskupovaní sa výrazy zamieňajú tak, že výrazy, ktoré sa majú zoskupiť, sa vo výraze objavia vedľa seba. Potom môžu byť uvedené v zátvorkách.

Príklad 11

Vezmime si výraz 5 + 7 + 1 ... Ak zoskupíme prvý výraz s tretím, dostaneme (5 + 1) + 7 .

Zoskupovanie faktorov sa vykonáva podobne ako zoskupovanie pojmov.

Príklad 12

V práci 2 3 4 5 môžeme zoskupiť prvý faktor s tretím a druhý so štvrtým a dospejeme k výrazu (2 4) (3 5)... A ak by sme zoskupili prvý, druhý a štvrtý faktor, dostali by sme výraz (2 3 5) 4.

Pojmy a faktory, ktoré sú zoskupené, môžu byť reprezentované prvočíslami aj výrazmi. Pravidlá zoskupovania boli podrobne rozobraté v téme „Zoskupovanie pojmov a faktorov“.

Nahrádzanie rozdielov súčtami, čiastkovými súčinmi a naopak

Nahradenie rozdielov súčtami bolo možné vďaka nášmu oboznámeniu sa s opačnými číslami. Teraz odčítanie od čísla ačísla b možno považovať za doplnok k číslu ačísla - b... Rovnosť a - b = a + (- b) možno považovať za spravodlivé a na jeho základe nahradiť rozdiely sumami.

Príklad 13

Vezmime si výraz 4 + 3 − 2 , v ktorom je rozdiel čísel 3 − 2 môžeme zapísať ako súčet 3 + (− 2) ... Dostaneme 4 + 3 + (− 2) .

Príklad 14

Všetky rozdiely vo výraze 5 + 2 x - x 2 - 3 x 3 - 0, 2 môžu byť nahradené sumami ako 5 + 2 x + (- x 2) + (- 3 x 3) + (- 0, 2).

Z akýchkoľvek rozdielov môžeme prejsť na súčty. Podobne môžeme vykonať spätnú výmenu.

Nahradenie delenia násobením prevrátenou hodnotou deliteľa umožňuje koncept vzájomne prevrátených čísel. Táto transformácia môže byť napísaná pomocou rovnosti a: b = a (b - 1).

Toto pravidlo bolo použité ako základ pre pravidlo na delenie obyčajných zlomkov.

Príklad 15

Súkromné 1 2: 3 5 možno nahradiť produktom formulára 1 2 5 3.

Analogicky možno delenie nahradiť násobením.

Príklad 16

V prípade výrazu 1 + 5: x: (x + 3) nahradiť delenie za X možno vynásobiť 1 x... Rozdelenie podľa x + 3 môžeme nahradiť násobením 1 x + 3... Transformácia nám umožňuje získať výraz zhodný s originálom: 1 + 5 · 1 x · 1 x + 3.

Nahradenie násobenia delením sa vykonáva podľa schémy a b = a: (b - 1).

Príklad 17

Vo výraze 5 x x 2 + 1 - 3 možno násobenie nahradiť delením ako 5: x 2 + 1 x - 3.

Vykonávanie akcií na číslach

Vykonávanie akcií s číslami dodržiava pravidlo poradia akcií. Po prvé, akcie sa vykonávajú s mocninami čísel a koreňmi čísel. Potom nahradíme logaritmy, trigonometrické a iné funkcie ich hodnotami. Potom sa vykonajú akcie v zátvorkách. A potom je možné vykonávať všetky ostatné akcie zľava doprava. Je dôležité mať na pamäti, že násobenie a delenie sa vykonáva pred sčítaním a odčítaním.

Operácie s číslami vám umožňujú previesť pôvodný výraz na identický rovnaký.

Príklad 18

Prepíšte výraz 3 · 2 3 - 1 · a + 4 · x 2 + 5 · x, pričom vykonajte všetky možné akcie s číslami.

Riešenie

V prvom rade si dajme pozor na stupeň 2 3 a root 4 a vypočítajte ich hodnoty: 2 3 = 8 a 4 = 2 2 = 2.

Dosaďte získané hodnoty do pôvodného výrazu a získajte: 3 · (8 - 1) · a + 2 · (x 2 + 5 · x).

Teraz urobme akcie v zátvorkách: 8 − 1 = 7 ... A prejdite na výraz 3 7 a + 2 (x 2 + 5 x).

Zostáva nám vykonať násobenie čísel 3 a 7 ... Získame: 21 a + 2 (x 2 + 5 x).

odpoveď: 3 2 3 - 1 a + 4 x 2 + 5 x = 21 a + 2 (x 2 + 5 x)

Akciám s číslami môžu predchádzať iné typy identických transformácií, ako napríklad zoskupovanie čísel alebo rozširovanie zátvoriek.

Príklad 19

Vezmime si výraz 3 + 2 (6: 3) x (y 3 4) - 2 + 11.

Riešenie

Najprv nahradíme podiel v zátvorkách 6: 3 na jeho hodnote 2 ... Dostaneme: 3 + 2 2 x (y 3 4) - 2 + 11.

Rozšírime zátvorky: 3 + 2 2 x (y 3 4) - 2 + 11 = 3 + 2 2 x y 3 4 - 2 + 11.

Zoskupme číselné faktory v produkte, ako aj pojmy, ktoré sú číslami: (3 - 2 + 11) + (2 2 4) x y 3.

Vykonajte akcie v zátvorkách: (3 - 2 + 11) + (2 2 4) x y 3 = 12 + 16 x y 3

odpoveď:3 + 2 (6: 3) x (y 3 4) - 2 + 11 = 12 + 16 x y 3

Ak pracujeme s číselnými výrazmi, tak cieľom našej práce bude nájsť význam výrazu. Ak transformujeme výrazy s premennými, potom bude cieľom nášho konania výraz zjednodušiť.

Vypočítajte spoločný faktor

V prípadoch, keď majú výrazy vo výraze rovnaký faktor, môžeme tento spoločný faktor vyňať zo zátvoriek. Aby sme to dosiahli, musíme najprv reprezentovať pôvodný výraz ako súčin spoločného činiteľa a výrazu v zátvorkách, ktorý pozostáva z pôvodných členov bez spoločného činiteľa.

Príklad 20

Číselne 2 7 + 2 3 môžeme vyňať spoločný faktor 2 zátvorkách a získajte identicky správne vyjadrenie tvaru 2 (7 + 3).

Pravidlá pre uvedenie spoločného faktora mimo zátvorky si môžete osviežiť v príslušnej časti nášho zdroja. Materiál podrobne rozoberá pravidlá pre uvedenie spoločného faktora mimo zátvorky a poskytuje množstvo príkladov.

Zníženie podobných výrazov

Teraz prejdime k sumám, ktoré obsahujú podobné výrazy. Existujú dve možnosti: súčty obsahujúce rovnaké výrazy a súčty, ktorých výrazy sa líšia číselným koeficientom. Akcie so sumami obsahujúcimi takéto podmienky sa nazývajú zníženie takýchto podmienok. Vykonáva sa takto: vyberieme všeobecnú časť písmena mimo zátvoriek a vypočítame súčet číselných koeficientov v zátvorkách.

Príklad 21

Zvážte výraz 1 + 4 x - 2 x... Môžeme dať doslovnú časť x mimo zátvorky a dostať výraz 1 + x (4 - 2)... Vypočítajme hodnotu výrazu v zátvorke a dostaneme súčet tvaru 1 + x · 2.

Nahradenie čísel a výrazov identicky rovnakými výrazmi

Čísla a výrazy, z ktorých sa skladá pôvodný výraz, možno nahradiť identicky rovnakými výrazmi. Takáto transformácia pôvodného výrazu vedie k výrazu identicky rovnakému ako jemu.

Príklad 22 Príklad 23

Zvážte výraz 1 + a 5, v ktorom môžeme stupeň 5 nahradiť identicky rovnakým súčinom, napríklad tvaru a a 4... To nám dá výraz 1 + a až 4.

Vykonaná transformácia je umelá. Zmysel to má len pri príprave na ďalšie premeny.

Príklad 24

Zvážte transformáciu súčtu 4 x 3 + 2 x 2... Tu je termín 4 x 3 si môžeme predstaviť ako dielo 2 x 2 2 x... Výsledkom je, že pôvodný výraz nadobúda formu 2 x 2 2 x + 2 x 2... Teraz môžeme vybrať spoločný faktor 2 x 2 a vložte ho mimo zátvorky: 2 x 2 (2 x + 1).

Pridajte a odčítajte rovnaké číslo

Súčasné sčítanie a odčítanie rovnakého čísla alebo výrazu je umelá technika transformácie výrazov.

Príklad 25

Zvážte výraz x 2 + 2 x... Môžeme od neho jednu pripočítať alebo odčítať, čo nám umožní v budúcnosti vykonať ešte jednu identickú transformáciu - vybrať druhú mocninu binomu: x 2 + 2 x = x 2 + 2 x + 1 - 1 = (x + 1) 2 - 1.

Ak si všimnete chybu v texte, vyberte ju a stlačte Ctrl + Enter

Ak chcete použiť ukážku prezentácií, vytvorte si účet Google (účet) a prihláste sa doň: https://accounts.google.com

Popisy snímok:

identity. Identické transformácie výrazov. 7. trieda.

Nájdite hodnotu výrazov na x = 5 a y = 4 3 (x + y) = 3 (5 + 4) = 3 * 9 = 27 3x + 3y = 3 * 5 + 3 * 4 = 27 Nájdite hodnotu výrazy na x = 6 a y = 5 3 (x + y) = 3 (6 + 5) = 3 * 11 = 33 3x + 3y = 3 * 6 + 3 * 5 = 33

ZÁVER: Dosiahli sme rovnaký výsledok. Z distribučnej vlastnosti vyplýva, že vo všeobecnosti pre všetky hodnoty premenných sú hodnoty výrazov 3 (x + y) a 3x + 3y rovnaké. 3 (x + y) = 3x + 3r

Uvažujme teraz o výrazoch 2x + y a 2xy. pre x = 1 a y = 2 nadobúdajú rovnaké hodnoty: 2x + y = 2 * 1 + 2 = 4 2xy = 2 * 1 * 2 = 4 pre x = 3, y = 4 hodnoty výrazov sú rôzne 2x + y = 2 * 3 + 4 = 10 2xy = 2 * 3 * 4 = 24

ZÁVER: Výrazy 3 (x + y) a 3x + 3y sú zhodne rovnaké, ale výrazy 2x + y a 2xy zhodne rovnaké nie sú. Definícia: Dva výrazy, ktorých hodnoty sú rovnaké pre akékoľvek hodnoty premenných, sa nazývajú identicky rovnaké.

IDENTITA Rovnosť 3 (x + y) a 3x + 3y platí pre všetky hodnoty x a y. Takéto rovnosti sa nazývajú identity. Definícia: Rovnosť, ktorá platí pre akékoľvek hodnoty premenných, sa nazýva identita. Za identity sa považujú aj skutočné číselné rovnosti. S identitami sme sa už stretli.

Identity sú rovnosti, ktoré vyjadrujú základné vlastnosti akcií na číslach. a + b = b + a ab = ba (a + b) + c = a + (b + c) (ab) c = a (bc) a (b + c) = ab + ac

Môžete uviesť ďalšie príklady identít: a + 0 = a a * 1 = a a + (-a) = 0 a * (- b) = - ab a- b = a + (- b) (-a) * ( - b) = ab Nahradenie jedného výrazu iným, identicky rovnakým výrazom, sa nazýva konverzia identity alebo jednoducho konverzia výrazu.

Ak chcete zadať takéto výrazy, musíte pridať ich koeficienty a vynásobiť výsledok celkovou časťou písmena. Príklad 1. Dajme podobné výrazy 5x + 2x-3x = x (5 + 2-3) = 4x

Ak je pred zátvorkami znamienko plus, zátvorky možno vynechať, pričom znamienko každého výrazu zostane v zátvorkách. Príklad 2. Rozviňme zátvorky vo výraze 2а + (b -3 c) = 2 a + b - 3 c

Ak je pred zátvorkami znamienko mínus, zátvorky možno vynechať zmenou znamienka každého výrazu v zátvorkách. Príklad 3. Otvorme zátvorky vo výraze a - (4 b - c) = a - 4 b + c

Domáca úloha: str.5, č.91, 97, 99 Ďakujeme za lekciu!

K téme: metodologický vývoj, prezentácie a poznámky

Metodika prípravy študentov na Jednotnú štátnu skúšku v časti „Výrazy a výrazová transformácia“

Tento projekt bol vypracovaný s cieľom pripraviť žiakov na štátne skúšky v 9. ročníku a ďalej na jednotnú štátnu skúšku v 11. ročníku ....

Obsah lekcie

Umocnenie dvojčlena

Binom je polynóm s dvoma členmi. V predchádzajúcich lekciách sme zvýšili dvojčlen na druhú a tretiu mocninu, čím sme získali skrátené vzorce násobenia:

(a + b) 2 = a 2 + 2ab + b 2

(a + b) 3 = a 3 + 3a 2 b + 3ab 2 + b 3

Ale dvojčlen môže byť zvýšený nielen na druhý a tretí stupeň, ale aj na štvrtý, piaty alebo vyšší stupeň.

Zostavme si napríklad binomiku a + b do štvrtého stupňa:

(a + b) 4

Tento výraz predstavujeme ako súčin dvojčlenky a + b a kocka tej istej dvojčlenky

(a + b)(a+ b) 3

Kofaktor ( a + b) 3 možno nahradiť pravou stranou vzorca kocky pre súčet dvoch výrazov. Potom dostaneme:

(a + b)(a 3 + 3a 2 b + 3ab 2 + b 3)

A to je obvyklé násobenie polynómov. Poďme to vykonať:

Teda pri konštrukcii dvojčlenu a + bštvrtý stupeň je polynóm a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4

(a + b) 4 = a 4 + 4a 3 b + 6a 2 b 2 + 4ab 3 + b 4

Vztýčenie dvojčlena a + b do štvrtého stupňa môžete urobiť aj toto: reprezentujte výraz ( a + b) 4 ako súčin stupňov (a + b) 2 (a + b) 2

(a + b) 2 (a + b) 2

Ale výraz ( a + b) 2 sa rovná a 2 + 2ab + b 2 ... Nahradiť vo výraze (a + b) 2 (a + b) 2 druhé mocniny súčtu polynómom a 2 + 2ab + b 2

(a 2 + 2ab + b 2)(a 2 + 2ab + b 2)

A toto je opäť obvyklé násobenie polynómov. Poďme to vykonať. Dostaneme rovnaký výsledok ako predtým:

Umocnenie trojčlenky

Trojčlen je mnohočlen s tromi členmi. Napríklad výraz a + b + c je trojročné.

Niekedy môže vzniknúť úloha povýšiť trojfunkčné obdobie na moc. Napríklad odmocnime trojčlenku a + b + c

(a + b + c) 2

Dva výrazy v zátvorkách môžu byť uzavreté v zátvorkách. Napríklad uzatvorme súčet a+ b v zátvorkách:

((a + b) + c) 2

V tomto prípade suma a + b sa bude považovať za jedného člena. Potom sa ukáže, že nekvadratúrujeme trojročné, ale dvojročné. Sum a + b bude prvým členom a členom c- druhý člen. A už vieme, ako odmocniť dvojčlen. Na tento účel môžete použiť vzorec pre druhú mocninu súčtu dvoch výrazov:

(a + b) 2 = a 2 + 2ab + b 2

Aplikujme tento vzorec na náš príklad:

Rovnakým spôsobom môžete odmocniť polynóm pozostávajúci zo štyroch alebo viacerých členov. Napríklad odmocni polynóm a + b + c + d

(a + b + c + d) 2

Polynóm predstavujeme ako súčet dvoch výrazov: a + b a c + d... Aby sme to dosiahli, uvádzame ich v zátvorkách:

((a + b) + (c + d)) 2

Teraz použijeme vzorec pre druhú mocninu súčtu dvoch výrazov:

Izolácia úplného štvorca od štvorcového trojčlenu

Ďalšou identickou transformáciou, ktorá môže byť užitočná pri riešení úloh, je výber úplného štvorca zo štvorcového trojčlenu.

Štvorcový trojčlen je trojčlen druhého stupňa. Napríklad nasledujúce tri výrazy sú štvorcové:

Myšlienkou izolácie úplného štvorca od takýchto trojčlenov je reprezentovať pôvodný štvorcový trojčlen vo forme výrazu ( a + b) 2 + c, kde ( a + b) 2 je úplný štvorec a c - nejaký číselný alebo doslovný výraz.

Vyberme napríklad úplný štvorec z trojčlenu 4X 2 + 16X+ 19 .

Najprv musíte vytvoriť výraz formulára a 2 + 2ab+ b 2 ... Postavíme ho z trojčlenu 4X 2 + 16X+ 19 ... Najprv si definujme, ktorí členovia budú hrať rolu premenných a a b

Úloha premennej a bude hrať člena 2 X od prvého členu trojčlenky 4X 2 + 16X+ 19 , konkrétne 4 X 2 sa získa, ak 2 X námestie:

(2X) 2 = 4X 2

Takže premenná a sa rovná 2 X

a = 2X

Teraz sa vrátime k pôvodnému trojčlennému členeniu a hneď venujeme pozornosť výrazu 16 X... Tento výraz je dvojitým súčinom prvého výrazu a(v našom prípade je to 2 X) a druhý nám zatiaľ neznámy výraz b. Na jeho miesto dočasne umiestnime otáznik:

2 × 2 X × ? = 16X

Ak sa pozriete pozorne na výraz 2 × 2 X × ? = 16X , potom je intuitívne jasné, že výraz b v tejto situácii je číslo 4, pretože výraz 2 × 2 X rovná sa 4 X a získať 16 X treba vynásobiť 4 X do 4.

2 × 2 X × 4 = 16X

Preto sme dospeli k záveru, že premenná b rovná sa 4

b = 4

To znamená, že výrazom bude náš úplný štvorec (2X) 2 + 2 × 2 X× 4 + 4 2

Teraz sme pripravení vybrať úplný štvorec z trojčlenu. 4X 2 + 16X+ 19 .

Takže späť k pôvodnému trinomu 4X 2 + 16X+ 19 a pokúsime sa do nej opatrne zaviesť kompletný štvorec, ktorý sme dostali (2X) 2 + 2 × 2 X× 4 + 4 2

4X 2 + 16X+ 19 =

Namiesto 4 X 2 píšeme (2 X) 2

4X 2 + 16X+ 19 = (2X) 2

4X 2 + 16X+ 19 = (2X) 2 + 2 × 2 X× 4

4X 2 + 16X+ 19 = (2X) 2 + 2 × 2 X× 4 + 4 2

A keď prepíšeme výraz 19 tak, ako je:

4X 2 + 16X + 19 = (2X) 2 + 2 × 2 X× 4 + 4 2 + 19

Teraz venujme pozornosť skutočnosti, že získaný polynóm (2X) 2 + 2 × 2 X× 4 + 4 2 + 19 nie totožné s pôvodným trojdobým 4X 2 + 16X+ 19 ... Môžete to overiť uvedením polynómu (2X) 2 + 2 × 2 X× 4 + 4 2 + 19 do štandardného zobrazenia:

(2X) 2 + 2 × 2 X× 4 + 4 2 + 19 = 4 X 2 + 16X + 4 2 + 19

Vidíme, že dostaneme polynóm 4X 2 + 16X+ 4 2 + 19 , ale malo to dopadnúť 4X 2 + 16X+ 19 ... Dôvodom je skutočnosť, že termín 4 2 bol umelo implantovaný do pôvodného trojročného obdobia, aby sa vytvoril úplný štvorec trojčlenného obdobia. 4X 2 + 16X+ 19 .

4X 2 + 16X + 19 = (2X) 2 + 2 × 2 X× 4 + 4 2 − 4 2 + 19

Teraz výraz (2X) 2 + 2 × 2 X× 4 + 4 2 možno zbaliť, to znamená napísať vo forme ( a + b) 2. V našom prípade dostaneme výraz (2 X+ 4) 2

4X 2 + 16X + 19 = (2X) 2 + 2 × 2 X× 4 + 4 2 - 4 2 + 19 = (2X + 4) 2 − 4 2 + 19

Zvyšné členy −4 2 a 19 možno pridať. −4 2 je −16, teda −16 + 19 = 3

4X 2 + 16X + 19 = (2X) 2 + 2 × 2 X× 4 + 4 2 - 4 2 + 19 = (2X + 4) 2 − 4 2 + 19 = (2X+ 4) 2 + 3

znamená, 4X 2 + 16X+ 19 = (2X + 4) 2 + 3

Príklad 2... Vyberte úplný štvorec zo štvorcového trojčlenu X 2 + 2X+ 2

Najprv vytvoríme výraz formulára a 2 + 2 ab + b 2. Úloha premennej a v tomto prípade x hrá, pretože X 2 = X 2 .

Ďalší člen pôvodnej trojčlenky 2 X prepíšte vo forme zdvojeného súčinu prvého výrazu (máme X) a druhý výraz b(toto bude 1).

2 × X× 1 = 2 X

Ak b= 1, potom výraz X 2 + 2X+ 1 2 .

Teraz sa vráťme k pôvodnému štvorcovému trojčlenu a vložme doň celý štvorec. X 2 + 2X+ 1 2

X 2 + 2X+ 2 = X 2 + 2X+ 1 2 − 1 2 + 2 = (X+ 1) 2 + 1

Rovnako ako v predchádzajúcom príklade, člen b(v tomto príklade je to 1) po sčítaní sa okamžite odčítalo, aby sa zachovala hodnota pôvodnej trojčlenky.

Zvážte nasledujúci číselný výraz:

9 + 6 + 2

Hodnota tohto výrazu je 17

9 + 6 + 2 = 17

Skúsme v tomto číselnom vyjadrení vybrať úplný štvorec. Aby sme to dosiahli, najprv vytvoríme výraz formulára a 2 + 2ab+ b 2 ... Úloha premennej a v tomto prípade hrá číslo 3, pretože prvý člen výrazu 9 + 6 + 2, konkrétne 9, môže byť reprezentovaný ako 3 2.

Druhý člen 6 je reprezentovaný ako zdvojený súčin prvého člena 3 a druhého člena 1

2 × 3 × 1 = 6

Teda premenná b sa bude rovnať jednej. Potom výraz 3 2 + 2 × 3 × 1 + 1 2 bude dokonalý štvorec. Vložme to do pôvodného výrazu:

− 1 2 + 2

Zložme celý štvorec a možno pridať výrazy −1 2 a 2:

3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 − 1 2 + 2 = (3 + 1) 2 + 1

Výsledkom je výraz (3 + 1) 2 + 2, čo je stále 17

(3 + 1) 2 +1 = 4 2 + 1 = 17

Povedzme, že máme štvorec a dva obdĺžniky. Štvorec so stranou 3 cm, obdĺžnik so stranami 2 cm a 3 cm a obdĺžnik so stranami 1 cm a 2 cm

Vypočítajme plochu každého tvaru. Plocha štvorca bude 3 2 = 9 cm 2, plocha ružového obdĺžnika - 2 × 3 = 6 cm 2, plocha lila - 1 × 2 = 2 cm 2

Napíšme súčet plôch týchto obdĺžnikov:

9 + 6 + 2

Tento výraz možno chápať ako spojenie štvorca a dvoch obdĺžnikov do jedného tvaru:

Potom sa získa obrázok, ktorého plocha je 17 cm2. Zobrazený obrázok skutočne obsahuje 17 štvorcov so stranou 1 cm.

Pokúsme sa vytvoriť štvorec z existujúceho obrázku. Navyše najväčšie námestie. Na to použijeme časti z ružového a fialového obdĺžnika.

Ak chcete vytvoriť najväčší štvorec z existujúceho obrázku, môžete žltý štvorec ponechať nezmenený a pripevniť polovicu ružového obdĺžnika na spodok žltého štvorca:

Vidíme, že do vytvorenia úplného štvorca chýba ešte jeden štvorcový centimeter. Môžeme to vziať z lila obdĺžnika. Vezmite teda jeden štvorec z fialového obdĺžnika a pripevnite ho k veľkému štvorcu, ktorý sa vytvorí:

Teraz sa pozrime bližšie na to, k čomu sme dospeli. A to na žltej časti postavy a ružovej časti, čím sa v skutočnosti zväčšil predchádzajúci žltý štvorec. Znamená to, že strana štvorca bola rovná 3 cm a táto strana bola zväčšená o 1 cm, čo v konečnom dôsledku viedlo k zväčšeniu plochy?

(3 + 1) 2

Výraz (3 + 1) 2 je 16, pretože 3 + 1 = 4 a 4 2 = 16. Rovnaký výsledok možno získať pomocou vzorca pre druhú mocninu súčtu dvoch výrazov:

(3 + 1) 2 = 3 2 + 6 + 1 = 9 + 6 + 1 = 16

Výsledný štvorec obsahuje 16 štvorcov.

Zostávajúci jeden štvorec z fialového obdĺžnika môže byť pripojený k výslednému veľkému štvorcu. Veď pôvodne išlo o jedinú figúrku:

(3 + 1) 2 + 1

Pripojenie malého štvorca k existujúcemu veľkému štvorcu je opísané výrazom (3 + 1) 2 + 1. A toto je výber celého štvorca z výrazu 9 + 6 + 2

9 + 6 + 2 = 3 2 + 6 + 2 = 3 2 + 2 × 3 × 1 + 1 2 - 1 2 + 2 = (3 + 1) 2 + 1

Výraz (3 + 1) 2 + 1, podobne ako výraz 9 + 6 + 2, je 17. V skutočnosti je plocha vytvorenej postavy 17 cm 2.

Príklad 4... Urobme výber úplného štvorca zo štvorcového trojčlenu X 2 + 6X + 8

X 2 + 6X + 8 = X 2 + 2 × X× 3 + 3 2 - 3 2 + 8 = ( X + 3) 2 − 1

V niektorých príkladoch pri zostavovaní výrazu a 2 + 2ab+ b 2 nie je možné okamžite určiť hodnoty premenných a a b .

Vyberme napríklad úplný štvorec zo štvorcového trojčlenu X 2 + 3X+ 2

Variabilné a sa viaže na X... Druhý termín 3 X nemožno reprezentovať ako zdvojený súčin prvého a druhého výrazu. V tomto prípade by sa mal druhý člen vynásobiť 2 a aby sa hodnota pôvodného polynómu nezmenila, okamžite vydeľte 2. Bude to vyzerať takto.

Rovnice

Ako riešiť rovnice?

V tejto časti si pripomenieme (alebo preštudujeme – ako ktokoľvek iný) najelementárnejšie rovnice. Čo je teda rovnica? Z ľudského hľadiska ide o nejaký druh matematického vyjadrenia, kde je znamienko rovnosti a neznáme. Čo sa zvyčajne označuje písmenom "X". Vyriešte rovnicu je nájsť také hodnoty x, ktoré pri dosadení do počiatočné výraz, nám dá správnu identitu. Pripomínam, že identita je výraz, ktorý nevzbudzuje pochybnosti ani u človeka absolútne nezaťaženého matematickými znalosťami. Napríklad 2 = 2, 0 = 0, ab = ab atď. Ako teda riešite rovnice? Poďme na to.

Sú tam všelijaké rovnice (to som bol prekvapený, však?). Ale všetku ich nekonečnú rozmanitosť možno rozdeliť iba do štyroch typov.

4. Iné.)

Všetko ostatné, samozrejme, najviac, áno...) To zahŕňa kubické, exponenciálne, logaritmické, trigonometrické a všetky ostatné. Budeme s nimi úzko spolupracovať v príslušných sekciách.

Hneď musím povedať, že niekedy sa rovnice prvých troch typov zamotajú tak, že ich ani nespoznáte ... Nič. Naučíme sa, ako ich odreagovať.

A prečo potrebujeme tieto štyri typy? A potom čo lineárne rovnice sú riešené jedným spôsobom, námestie iní, zlomkové racionálne - tretina, a odpočinok vôbec sa neodvažuj! No nejde o to, že by sa vôbec nerozhodovali, nemal som urážať matematiku.) Ide len o to, že majú svoje špeciálne techniky a metódy.

Ale pre akékoľvek (opakujem - pre akýkoľvek!) rovnice majú spoľahlivý a bezproblémový základ na riešenie. Funguje kdekoľvek a kedykoľvek. Tento základ - Znie to strašidelne, ale vec je veľmi jednoduchá. A veľmi (veľmi!) dôležité.

V skutočnosti riešenie rovnice pozostáva práve z týchto transformácií. 99 %. Odpoveď na otázku: " Ako riešiť rovnice?"klame, práve v týchto premenách. Je náznak jasný?)

Identické transformácie rovníc.

V akékoľvek rovnice na nájdenie neznámeho je potrebné pôvodný príklad transformovať a zjednodušiť. A to tak, že pri zmene vzhľadu podstata rovnice sa nezmenila. Takéto premeny sa nazývajú identické alebo ekvivalent.

Všimnite si, že tieto transformácie sú presne na rovnice. V matematike stále existujú rovnaké transformácie výrazov. Toto je iná téma.

Teraz si zopakujeme all-all-all basic identické transformácie rovníc.

Základné, pretože sa na ne dá aplikovať akýkoľvek rovnice - lineárne, kvadratické, zlomkové, trigonometrické, exponenciálne, logaritmické atď. atď.

Prvá transformácia identity: môžete pridať (odčítať) na obe strany akejkoľvek rovnice akýkoľvek(ale to isté!) číslo alebo výraz (vrátane výrazu s neznámou!). To nemení podstatu rovnice.

Mimochodom, túto transformáciu ste neustále používali, len ste si mysleli, že niektoré pojmy prenášate z jednej strany rovnice na druhú so zmenou znamienka. Typ:

Záležitosť je známa, prenesieme tieto dva doprava a dostaneme:

V skutočnosti vy odvezený z oboch strán rovnice dva. Výsledok je rovnaký:

x + 2 - 2 = 3 - 2

Presun pojmov zľava doprava so zmenou znamienka je jednoducho skrátená verzia prvej identickej transformácie. A prečo potrebujeme také hlboké znalosti? - pýtaš sa. Rovnice sú nízke. Pohni sa, preboha. Len nezabudnite zmeniť znamenie. Ale v nerovnostiach môže byť zvyk prenosu mätúci...

Druhá transformácia identity: obe strany rovnice možno vynásobiť (vydeliť) rovnako nenulovéčíslo alebo výraz. Už tu sa objavuje pochopiteľné obmedzenie: násobiť nulou je hlúposť, ale deliť sa vôbec nedá. Túto transformáciu použijete, keď robíte niečo skvelé

Je to jasný biznis X= 2. Ako ste to našli? Výberom? Alebo sa len rozsvietilo? Aby ste sa nezdvihli a nečakali na pochopenie, musíte pochopiť, že práve rozdelil obe strany rovnice o 5. Pri delení ľavej strany (5x) sa päťka zmenšila a zostalo čisté x. Čo sme potrebovali. A pri delení pravej strany (10) piatimi vyšla, samozrejme, dvojka.

To je všetko.

Je to smiešne, ale tieto dve (iba dve!) identické transformácie sú základom riešenia všetky matematické rovnice. Ako! Má zmysel pozrieť sa na príklady toho, čo a ako, nie?)

Príklady identických transformácií rovníc. Hlavné problémy.

Začnime s prvý identická transformácia. Pohyb doľava-doprava.

Príklad pre najmladších.)

Povedzme, že potrebujete vyriešiť nasledujúcu rovnicu:

3-2x = 5-3x

Pamätajte na kúzlo: "s x - doľava, bez x - doprava!" Toto kúzlo je návodom, ako použiť prvú identickú transformáciu.) Aký výraz s x máme vpravo? 3x? Odpoveď je nesprávna! Po našej pravici - 3x! Mínus tri x! Preto pri pohybe doľava sa znamienko zmení na plus. Ukáže sa:

3-2x + 3x = 5

Takže X boli zhromaždené na hromade. Poďme k číslam. Naľavo je trojka. aké je tvoje znamenie? Odpoveď „s nie“ sa neprijíma!) Pred trojkou sa naozaj nič nekreslí. A to znamená, že pred trojkou je plus. Matematici teda súhlasili. Nič nie je napísané, takže plus. Preto sa trojka prenesie na pravú stranu s mínusom. Dostaneme:

-2x + 3x = 5-3

Zostávajú len maličkosti. Vľavo - prineste podobné, vpravo - počítajte. Odpoveď dostanete okamžite:

V tomto príklade stačila jedna identická transformácia. Druhý nebol potrebný. No dobre.)

Príklad pre starších.)

Ak sa vám táto stránka páči...

Mimochodom, mám pre vás niekoľko ďalších zaujímavých stránok.)

Môžete si precvičiť riešenie príkladov a zistiť svoju úroveň. Okamžité overovacie testovanie. Učenie - so záujmom!)

môžete sa zoznámiť s funkciami a deriváciami.