Poznámky z prednášok mechaniky. Technická mechanika
1 snímka
Kurz prednášok z teoretickej mechaniky Dynamika (I časť) Bondarenko A.N. Moskva - 2007 Elektronický kurz bol napísaný na základe prednášok autora pre študentov študujúcich v odboroch SZhD, PGS a SDM na NIIZhT a MIIT (1974-2006). Vzdelávací materiál zodpovedá kalendárnym plánom v rozsahu troch semestrov. Ak chcete plne implementovať efekty animácie počas prezentácie, musíte použiť prehliadač Power Point, ktorý nie je nižší ako ten, ktorý je zabudovaný do balíka Microsoft Office operačného systému Windows-XP Professional. Pripomienky a návrhy je možné posielať na e-mail: [chránený e-mailom]. Moskva Štátna univerzitaŽeleznice (MIIT) Katedra teoretickej mechaniky Vedecko-technické centrum dopravných technológií

2 snímka
Obsah Prednáška 1. Úvod do dynamiky. Zákony a axiómy dynamiky hmotných bodov. Základná rovnica dynamiky. Diferenciálne a prirodzené pohybové rovnice. Dve hlavné úlohy dynamiky. Príklady riešenia priamej úlohy dynamiky Prednáška 2. Riešenie inverznej úlohy dynamiky. Všeobecné pokyny na riešenie inverznej úlohy dynamiky. Príklady riešenia inverznej úlohy dynamiky. Pohyb telesa vrhaného pod uhlom k horizontu bez zohľadnenia odporu vzduchu. Prednáška 3. Priamočiare kmity hmotného bodu. Podmienka pre vznik oscilácií. Klasifikácia vibrácií. Voľné vibrácie bez zohľadnenia síl odporu. tlmené vibrácie. Zníženie oscilácie. Prednáška 4. Vynútené kmity hmotného bodu. Rezonancia. Vplyv odporu na pohyb pri vynútených vibráciách. Prednáška 5. Relatívny pohyb hmotného bodu. Zotrvačné sily. Konkrétne prípady pohybu pre rôzne druhy prenosného pohybu. Vplyv rotácie Zeme na rovnováhu a pohyb telies. Prednáška 6. Dynamika mechanického systému. mechanický systém. Vonkajšie a vnútorné sily. Ťažisko systému. Veta o pohybe ťažiska. Ochranné zákony. Príklad riešenia úlohy použitia vety o pohybe ťažiska. Prednáška 7. Impulz sily. Množstvo pohybu. Veta o zmene hybnosti. Ochranné zákony. Eulerova veta. Príklad riešenia problému použitia vety o zmene hybnosti. moment hybnosti. Veta o zmene momentu hybnosti Prednáška 8. Zákony zachovania. Prvky teórie momentov zotrvačnosti. Kinetický moment tuhého telesa. Diferenciálna rovnica rotácie tuhého telesa. Príklad riešenia problému použitia vety o zmene momentu hybnosti sústavy. Elementárna teória gyroskopu. Odporúčaná literatúra 1. Yablonsky A.A. Kurz teoretickej mechaniky. Časť 2. M.: Vysoká škola. 1977. 368 s. 2. Meshchersky I.V. Zbierka úloh z teoretickej mechaniky. M.: Veda. 1986 416 s. 3. Zbierka úloh pre ročníkové práce/ Ed. A.A. Yablonsky. M.: Vysoká škola. 1985. 366 s. 4. Bondarenko A.N. „Teoretická mechanika v príkladoch a úlohách. Dynamics“ (elektronická príručka www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004

3 snímka
Prednáška 1 Dynamika je časť teoretickej mechaniky, ktorá študuje mechanický pohyb z najvšeobecnejšieho hľadiska. Pohyb sa uvažuje v súvislosti so silami pôsobiacimi na objekt. Sekcia pozostáva z troch sekcií: Dynamika hmotného bodu Dynamika Dynamika mechanického systému Analytická mechanika ■ Dynamika bodu - študuje pohyb hmotného bodu s prihliadnutím na sily, ktoré tento pohyb spôsobujú. Hlavným predmetom je hmotný bod – hmotné teleso s hmotou, ktorej rozmery možno zanedbať. Základné predpoklady: - existuje absolútny priestor (má čisto geometrické vlastnosti, ktoré nezávisia od hmoty a jej pohybu. - existuje absolútny čas (nezávisí od hmoty a jej pohybu). Z toho vyplýva: - existuje absolútne nehybná vzťažná sústava - čas nezávisí od pohybu vzťažnej sústavy - hmotnosti pohybujúcich sa bodov nezávisia od pohybu vzťažnej sústavy Tieto predpoklady sa používajú v klasickej mechanike vytvorenej Galileom a Newtonom Stále má pomerne široký záber, keďže mechanické systémy uvažované v aplikovaných vedách nemajú také veľké hmotnosti a rýchlosti pohybu, pri ktorých je potrebné brať do úvahy ich vplyv na geometriu priestoru, času, pohybu, ako napr. sa vykonáva v relativistickej mechanike (teória relativity) ■ Základné zákony dynamiky - prvýkrát objavené Galileom a formulované Newtonom tvoria základ všetkých metód na popis a analýzu pohybu mechanických systémov a ich dynamickej interakcie pôsobenie pod vplyvom rôznych síl. ■ Zákon zotrvačnosti (Galileov-Newtonov zákon) - Izolovaný hmotný bod telesa si zachováva stav pokoja alebo rovnomerného priamočiareho pohybu, kým ho aplikované sily neprinútia tento stav zmeniť. To znamená ekvivalenciu stavu pokoja a pohybu zotrvačnosťou (Galileov zákon relativity). Vzťažná sústava, vo vzťahu ku ktorej je splnený zákon zotrvačnosti, sa nazýva inerciálna. Vlastnosť hmotného bodu snažiť sa udržať rýchlosť svojho pohybu (svoj kinematický stav) nezmenenú sa nazýva zotrvačnosť. ■ Zákon úmernosti sily a zrýchlenia (Základná rovnica dynamiky - Newtonov zákon II) - Zrýchlenie udelené hmotnému bodu silou je priamo úmerné sile a nepriamo úmerné hmotnosti tohto bodu: alebo Tu je m hmotnosť bodu (miera zotrvačnosti), meraná v kg, číselne rovná hmotnosti vydelenej gravitačným zrýchlením: F je pôsobiaca sila meraná v N (1 N udeľuje hmotnému bodu zrýchlenie 1 m/s2 1 kg, 1 N \u003d 1/9. 81 kg-s). ■ Dynamika mechanického systému – študuje pohyb množiny hmotných bodov a pevných telies, spojených všeobecnými zákonmi vzájomného pôsobenia, berúc do úvahy sily, ktoré tento pohyb spôsobujú. ■ Analytická mechanika – študuje pohyb nevoľných mechanických systémov pomocou všeobecných analytických metód. jeden

4 snímka
1. prednáška (pokračovanie - 1.2) Diferenciálne pohybové rovnice hmotného bodu: - diferenciálna pohybová rovnica bodu vo vektorovom tvare. - diferenciálne rovnice pohybu bodu v súradnicovom tvare. Tento výsledok možno získať formálnym premietnutím vektorovej diferenciálnej rovnice (1). Po zoskupení sa vektorový vzťah rozloží na tri skalárne rovnice: V súradnicovom tvare: Použijeme vzťah polomer-vektor so súradnicami a vektora sily s priemetmi: diferenciálna rovnica pohybu na prirodzených (pohyblivých) súradnicových osiach: alebo: - prirodzené pohybové rovnice bodu. ■ Základná rovnica dynamiky: - zodpovedá vektorovému spôsobu určenia pohybu bodu. ■ Zákon nezávislosti pôsobenia síl - Zrýchlenie hmotného bodu pri pôsobení viacerých síl sa rovná geometrickému súčtu zrýchlení bodu od pôsobenia každej zo síl zvlášť: alebo Platí zákon pre akýkoľvek kinematický stav telies. Sily interakcie pôsobiace na rôzne body (telesá) nie sú vyvážené. ■ Zákon o rovnosti akcie a reakcie (Newtonov zákon III) - Každá akcia zodpovedá rovnakej a opačne orientovanej reakcii: 2

5 snímka
Dva hlavné problémy dynamiky: 1. Priama úloha: Pohyb je daný (pohybové rovnice, trajektória). Je potrebné určiť sily, pri ktorých pôsobení dochádza k danému pohybu. 2. Inverzná úloha: Sú dané sily, pri ktorých pôsobení dochádza k pohybu. Je potrebné nájsť parametre pohybu (pohybové rovnice, trajektória pohybu). Obe úlohy sú riešené pomocou základnej rovnice dynamiky a jej premietnutia na súradnicové osi. Ak sa uvažuje o pohybe nevoľného bodu, potom sa rovnako ako v statike používa princíp uvoľnenia z väzieb. V dôsledku reakcie sa väzby zahrnú do zloženia síl pôsobiacich na hmotný bod. Riešenie prvého problému je spojené s operáciami diferenciácie. Riešenie inverznej úlohy vyžaduje integráciu zodpovedajúcich diferenciálnych rovníc, a to je oveľa náročnejšie ako diferenciácia. Inverzný problém je ťažší ako priamy problém. Riešenie priameho problému dynamiky - pozrime sa na príklady: Príklad 1. Kabína s hmotnosťou G výťahu je zdvíhaná lanom so zrýchlením a . Určite napätie kábla. 1. Vyberte objekt (výťahová kabína sa pohybuje dopredu a možno ju považovať za hmotný bod). 2. Spojenie (kábel) vyhodíme a nahradíme reakciou R. 3. Zostavte základnú rovnicu dynamiky: Určte reakciu kábla: Určte napnutie kábla: Pri rovnomernom pohybe kabíny ay = 0 a napätie lana sa rovná hmotnosti: T = G. Keď sa lano pretrhne T = 0 a zrýchlenie kabíny sa rovná zrýchleniu voľného pádu: ay = -g. 3 4. Základnú rovnicu dynamiky premietneme na os y: y Príklad 2. Hmotný bod m sa pohybuje po vodorovnej ploche (rovina Oxy) podľa rovníc: x = a coskt, y = b coskt. Určte silu pôsobiacu na bod. 1. Vyberte objekt (hmotný bod). 2. Spojenie (rovinu) zahodíme a nahradíme reakciou N. 3. Do sústavy síl pridáme neznámu silu F. 4. Zostavme základnú rovnicu dynamiky: 5. Premietnime základnú rovnicu dynamiky na x. osi y: Určte priemet sily: Modul sily: Smer kosinus : Veľkosť sily je teda úmerná vzdialenosti bodu od stredu súradníc a smeruje k stredu pozdĺž čiary spájajúcej bod so stredom. . Trajektória pohybu bodu je elipsa so stredom v počiatku: O r Prednáška 1 (pokračovanie - 1.3)

6 snímka
Prednáška 1 (pokračovanie 1.4) Príklad 3: Bremeno o hmotnosti G je zavesené na lane dĺžky l a pohybuje sa po kruhovej dráhe vo vodorovnej rovine určitou rýchlosťou. Uhol odchýlky kábla od vertikály sa rovná. Určte napnutie kábla a rýchlosť zaťaženia. 1. Vyberte objekt (náklad). 2. Spojenie (lano) zlikvidujte a nahraďte reakciou R. 3. Zostavte hlavnú rovnicu dynamiky: Z tretej rovnice určte reakciu kábla: Určte napnutie kábla: Dosaďte hodnotu reakcie lana, normálové zrýchlenie do druhej rovnice a určte rýchlosť zaťaženia: 4. Premietnite hlavnú rovnicu dynamika nápravy, n, b: Príklad 4: Automobil o hmotnosti G sa pohybuje po konvexnom moste (polomer zakrivenia je R ) s rýchlosťou V. Určte tlak auta na most. 1. Vyberieme objekt (auto, zanedbáme rozmery a považujeme ho za bod). 2. Spoj (hrubý povrch) zahodíme a nahradíme reakciami N a trecou silou Ffr. 3. Zostavíme základnú rovnicu dynamiky: 4. Na os n premietneme základnú rovnicu dynamiky: Odtiaľ určíme normálovú reakciu: Určíme tlak auta na most: Odtiaľ môžeme určiť rýchlosť. zodpovedajúce nulovému tlaku na mostíku (Q = 0): 4

7 snímka
Prednáška 2 Po dosadení zistených hodnôt konštánt dostaneme: Hmotný bod teda môže pri pôsobení toho istého systému síl vykonávať celú triedu pohybov určených počiatočnými podmienkami. Počiatočné súradnice zohľadňujú počiatočnú polohu bodu. Počiatočná rýchlosť, daná projekciami, zohľadňuje vplyv na jej pohyb po uvažovanom úseku trajektórie síl, ktoré na bod pôsobili pred príchodom do tohto úseku, t.j. počiatočný kinematický stav. Riešenie inverznej úlohy dynamiky - Vo všeobecnom prípade pohybu bodu sú sily pôsobiace na bod premenné, ktoré závisia od času, súradníc a rýchlosti. Pohyb bodu je opísaný systémom troch diferenciálnych rovníc druhého rádu: Po integrácii každej z nich bude existovať šesť konštánt C1, C2,…., C6: Hodnoty konštánt C1, C2,… ., C6 nájdeme zo šiestich počiatočných podmienok pri t = 0: Príklad 1 riešenia inverznej úlohy: Voľný hmotný bod s hmotnosťou m sa pohybuje pôsobením sily F, ktorá je konštantná čo do veľkosti a veľkosti. . V počiatočnom momente bola rýchlosť bodu v0 a zhodovala sa v smere so silou. Určte pohybovú rovnicu bodu. 1. Zostavíme základnú rovnicu dynamiky: 3. Znížime poradie derivácie: 2. Zvolíme kartézsky referenčný systém, pričom os x smerujeme v smere sily a na túto os premietneme hlavnú rovnicu dynamiky: alebo x y z 4. Oddeľte premenné: 5. Vypočítajte integrály z oboch častí rovnice : 6. Znázorňme priemet rýchlosti ako časovú deriváciu súradnice: 8. Vypočítajte integrály oboch častí rovnice: 7. Oddeľte premenné: 9. Na určenie hodnôt konštánt C1 a C2 použijeme počiatočné podmienky t = 0, vx = v0 , x = x0: Výsledkom je rovnica rovnomerne premenlivého pohybu (po os x): 5

8 snímka
Všeobecné pokyny na riešenie priamych a inverzných úloh. Postup riešenia: 1. Zostavenie diferenciálnej pohybovej rovnice: 1.1. Vyberte si súradnicový systém - pravouhlý (pevný) s neznámou trajektóriou pohybu, prirodzený (pohyblivý) so známou trajektóriou, napríklad kruh alebo priamka. V druhom prípade možno použiť jednu priamočiaru súradnicu. Referenčný bod by mal byť kombinovaný s počiatočnou polohou bodu (v t = 0) alebo s rovnovážnou polohou bodu, ak existuje, napríklad keď bod kolíše. 6 1.2. Nakreslite bod v polohe zodpovedajúcej ľubovoľnému časovému okamihu (pre t > 0) tak, aby súradnice boli kladné (s > 0, x > 0). Tiež predpokladáme, že projekcia rýchlosti v tejto polohe je tiež pozitívna. V prípade kmitov mení projekcia rýchlosti znamienko, napríklad pri návrate do rovnovážnej polohy. Tu treba predpokladať, že v uvažovanom časovom okamihu sa bod vzďaľuje od rovnovážnej polohy. Implementácia tohto odporúčania je dôležitá v budúcnosti pri práci s odporovými silami, ktoré závisia od rýchlosti. 1.3. Uvoľnite hmotný bod z väzieb, nahraďte ich pôsobenie reakciami, pridajte aktívne sily. 1.4. Napíšte základný zákon dynamiky vo vektorovej forme, premietnite na vybrané osi, vyjadrite dané alebo reaktívne sily v časových, súradnicových alebo rýchlostných premenných, ak od nich závisia. 2. Riešenie diferenciálnych rovníc: 2.1. Znížte deriváciu, ak rovnica nie je zredukovaná na kanonickú (štandardnú) formu. napríklad: alebo 2.2. Samostatné premenné, napríklad: alebo 2.4. Vypočítajte neurčité integrály na ľavej a pravej strane rovnice, napríklad: 2.3. Ak sú v rovnici tri premenné, potom vykonajte zmenu premenných, napríklad: a potom oddeľte premenné. Komentujte. Namiesto vyhodnocovania neurčitých integrálov je možné vyhodnotiť určité integrály s premennou hornou hranicou. Spodné hranice predstavujú počiatočné hodnoty premenné (počiatočné podmienky). Potom nie je potrebné samostatne hľadať konštantu, ktorá je automaticky zahrnutá do riešenia, napr.: Pomocou počiatočných podmienok, napr. t = 0, vx = vx0, určte konštantu integrácie: 2.5. Vyjadrite rýchlosť napríklad pomocou časovej derivácie súradnice a zopakujte kroky 2.2 - 2.4 Poznámka. Ak sa rovnica zredukuje na kanonickú formu, ktorá má štandardné riešenie, použije sa toto hotové riešenie. Konštanty integrácie sa stále nachádzajú z počiatočných podmienok. Pozri napríklad oscilácie (4. prednáška, s. 8). Prednáška 2 (pokračovanie 2.2)

9 snímka
2. prednáška (pokračovanie 2.3) Príklad 2 riešenia inverznej úlohy: Sila závisí od času. Po hladkej vodorovnej ploche sa začne bremeno hmotnosti P pohybovať pôsobením sily F, ktorej veľkosť je úmerná času (F = kt). Určte vzdialenosť prejdenú nákladom za čas t. 3. Zostavte základnú rovnicu dynamiky: 5. Zredukujte poradie derivácie: 4. Premietnite základnú rovnicu dynamiky na os x: alebo 7 6. Oddeľte premenné: 7. Vypočítajte integrály oboch častí rovnice. rovnica: 9. Predstavte priemet rýchlosti ako deriváciu súradnice vzhľadom na čas: 10. Vypočítajte integrály oboch častí rovnice: 9. Oddeľte premenné: 8. Určte hodnotu konštanty C1 z počiatočná podmienka t = 0, vx = v0=0: Výsledkom je pohybová rovnica (po osi x), ktorá udáva hodnotu prejdenej vzdialenosti za čas t: 1. Zvolíme referenčný systém (karteziánsky súradnice), aby teleso malo kladnú súradnicu: 2. Predmet pohybu berieme ako hmotný bod (teleso sa pohybuje dopredu), uvoľníme ho zo spojenia (referenčná rovina) a nahradíme reakciou (normálna reakcia a hladký povrch) : 11. Určte hodnotu konštanty C2 z počiatočnej podmienky t = 0, x = x0=0: Príklad 3 riešenia inverznej úlohy: Sila závisí od súradnice. Hmotný bod s hmotnosťou m je vrhaný smerom nahor z povrchu Zeme rýchlosťou v0. Gravitačná sila Zeme je nepriamo úmerná štvorcu vzdialenosti od bodu k ťažisku (stredu Zeme). Určte závislosť rýchlosti od vzdialenosti y od stredu Zeme. 1. Vzťažný systém (karteziánske súradnice) zvolíme tak, aby teleso malo kladnú súradnicu: 2. Zostavíme základnú rovnicu dynamiky: 3. Základnú rovnicu dynamiky premietneme na os y: alebo Koeficient úmernosti môže nájsť pomocou hmotnosti bodu na povrchu Zeme: R Preto diferenciál vyzerá takto: alebo 4. Znížte poradie derivácie: 5. Zmeňte premennú: 6. Oddeľte premenné: 7. Vypočítajte integrály oboch strán rovnice: 8. Dosaďte limity: Výsledkom je vyjadrenie rýchlosti v závislosti od súradnice y: Maximálnu výšku letu možno nájsť prirovnaním rýchlosti k nule: Maximálna výška letu keď sa menovateľ zmení na nulu: Odtiaľ pri nastavení polomeru Zeme a zrýchlení voľného pádu sa získa II kozmická rýchlosť:

10 snímka
2. prednáška (pokračovanie 2.4) Príklad 2 riešenia inverznej úlohy: Sila závisí od rýchlosti. Loď s hmotnosťou m mala rýchlosť v0. Odpor vody voči pohybu lode je úmerný rýchlosti. Určte čas, za ktorý klesne rýchlosť lode na polovicu po vypnutí motora, ako aj vzdialenosť, ktorú loď prejde do úplného zastavenia. 8 1. Vzťažný systém (karteziánske súradnice) zvolíme tak, aby teleso malo kladnú súradnicu: 2. Predmet pohybu berieme ako hmotný bod (loď sa pohybuje dopredu), oslobodíme ho od väzieb (voda) a nahradíme s reakciou (vztlaková sila – Archimedova sila), a tiež sila odporu voči pohybu. 3. Pridajte aktívnu silu (gravitáciu). 4. Zostavíme hlavnú rovnicu dynamiky: 5. Hlavnú rovnicu dynamiky premietneme na os x: alebo 6. Poradie derivácie znížime: 7. Oddelíme premenné: 8. Z oboch vypočítame integrály. časti rovnice: 9. Dosadíme limity: Získame výraz, ktorý dáva do súvisu rýchlosť a čas t, z ktorého môžete určiť čas pohybu: Čas pohybu, počas ktorého rýchlosť klesne na polovicu: Je zaujímavé je, že keď sa rýchlosť blíži k nule, čas pohybu má tendenciu k nekonečnu, t.j. konečná rýchlosť nemôže byť nulová. Prečo nie "perpetum mobile"? V tomto prípade je však prejdená vzdialenosť do zastávky konečná hodnota. Na určenie prejdenej vzdialenosti sa obrátime na výraz získaný po znížení rádu derivácie a vykonáme zmenu premennej: Po integrácii a dosadení limitov dostaneme: Vzdialenosť prejdená do zastavenia: ■ Pohyb bodu hodeného na uhol k horizontu v rovnomernom gravitačnom poli bez zohľadnenia odporu vzduchu Vylúčením času z pohybových rovníc získame rovnicu trajektórie: Čas letu určíme prirovnaním súradnice y k nule: Dosah letu sa určí dosadením čas letu:

11 snímka
3. prednáška Priamočiare kmity hmotného bodu - Kmitavý pohyb hmotného bodu nastáva za podmienky, že pôsobí vratná sila, ktorá má tendenciu vrátiť bod do rovnovážnej polohy pri akejkoľvek odchýlke od tejto polohy. 9 Existuje vratná sila, rovnovážna poloha je stabilná Žiadna vratná sila, rovnovážna poloha je nestabilná Žiadna vratná sila, rovnovážna poloha je indiferentná Smeruje vždy do rovnovážnej polohy, hodnota je priamo úmerná lineárnemu predĺženiu (skráteniu) pružiny, rovná sa odchýlke telesa od rovnovážnej polohy: c je koeficient tuhosti pružiny, číselne rovný sile pod ktorým pružina zmení svoju dĺžku o jednu, meranú v N/m v sústave SI. x y O Druhy kmitov hmotného bodu: 1. Voľné kmity (bez zohľadnenia odporu média). 2. Voľné kmity zohľadňujúce odpor média (tlmené kmity). 3. Nútené vibrácie. 4. Nútené kmity zohľadňujúce odpor média. ■ Voľné kmity - vznikajú pri pôsobení iba vratnej sily. Zapíšme si základný zákon dynamiky: Vyberme si súradnicový systém so stredom v rovnovážnej polohe (bod O) a premietnime rovnicu na os x: Výslednú rovnicu uveďme do štandardného (kanonického) tvaru: Táto rovnica je homogénna. lineárna diferenciálna rovnica druhého rádu, ktorej tvar riešenia je určený koreňmi charakteristiky rovnice získanej pomocou univerzálnej substitúcie: Korene charakteristickej rovnice sú imaginárne a rovné: Všeobecné riešenie diferenciálnej rovnice má tvar: Bodová rýchlosť: Počiatočné podmienky: Definujte konštanty: Takže rovnica voľných kmitov má tvar: Rovnica môže byť vyjadrená jednočlenným výrazom: kde a je amplitúda, - počiatočná fáza. Nové konštanty a a - súvisia s konštantami C1 a C2 vzťahmi: Definujme a a: Príčinou vzniku voľných kmitov je počiatočné posunutie x0 a/alebo počiatočná rýchlosť v0.

12 snímka
10 3. prednáška (pokračovanie 3.2) Tlmené kmity hmotného bodu - Kmitavý pohyb hmotného bodu nastáva za prítomnosti vratnej sily a sily odporu voči pohybu. Závislosť sily odporu voči pohybu od posunu alebo rýchlosti je určená fyzikálnou povahou média alebo spojenia, ktoré bráni pohybu. Najjednoduchšia závislosť je lineárna závislosť od rýchlosti (viskózneho odporu): - koeficient viskozity x y O z hodnôt koreňov: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - prípad vysokého viskózneho odporu: - skutočné korene, rôzne. alebo - tieto funkcie sú aperiodické: 3. n = k: - korene sú skutočné, násobné. tieto funkcie sú tiež aperiodické:

13 snímka
3. prednáška (pokračovanie 3.3) Klasifikácia riešení voľných kmitov. Pružinové spojenia. ekvivalentná tvrdosť. y y 11 Dif. Znak rovnice. Roots char. rovnica Riešenie diferenciálnej rovnice Graf nk n=k

14 snímka
4. prednáška Vynútené vibrácie hmotného bodu - Spolu s vratnou silou pôsobí periodicky sa meniaca sila, nazývaná rušivá sila. Rušivá sila môže mať rôznu povahu. Napríklad v konkrétnom prípade zotrvačný účinok nevyváženej hmoty m1 rotujúceho rotora spôsobuje harmonicky sa meniace priemetne síl: Hlavná rovnica dynamiky: Priemet rovnice dynamiky na os: Uveďme rovnicu do normy tvar: 12 Riešenie tejto nehomogénnej diferenciálnej rovnice sa skladá z dvoch častí x = x1 + x2: x1 je všeobecné riešenie príslušnej homogénnej rovnice a x2 je partikulárne riešenie nehomogénnej rovnice: Partikulárne riešenie vyberieme v tvare pravá strana: Výsledná rovnosť musí byť splnená pre ľubovoľné t . Potom: alebo Takto, s simultánne pôsobenie vratných a rušivých síl, hmotný bod vykonáva zložitý kmitavý pohyb, ktorý je výsledkom sčítania (superpozície) voľných (x1) a vynútených (x2) vibrácií. Ak p< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (vynútené kmity vysokej frekvencie), potom je fáza kmitov opačná ako fáza rušivej sily:

15 snímka
Prednáška 4 (pokračovanie 4.2) 13 Dynamický koeficient - pomer amplitúdy vynútených kmitov k statickej odchýlke bodu pri pôsobení konštantnej sily H = konšt.: Amplitúda vynútených kmitov: Statická odchýlka sa dá zistiť z rovnica rovnováhy: Tu: Preto: Na str< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (vysoká frekvencia vynútených kmitov) dynamický koeficient: Rezonancia - nastáva vtedy, keď sa frekvencia vynútených kmitov zhoduje s frekvenciou vlastných kmitov (p = k). Najčastejšie k tomu dochádza pri spustení a zastavení rotácie zle vyvážených rotorov namontovaných na elastických závesoch. Diferenciálna rovnica kmitov s rovnakými frekvenciami: Nie je možné prijať konkrétne riešenie vo forme pravej strany, pretože dostaneme lineárne závislé riešenie (pozri všeobecné riešenie). Všeobecné riešenie: Dosaďte v diferenciálnej rovnici: Zoberme si konkrétne riešenie v tvare a vypočítajme derivácie: Tak dostaneme riešenie: alebo Vynútené kmity pri rezonancii majú amplitúdu, ktorá sa úmerne času neobmedzene zvyšuje. Vplyv odporu na pohyb pri vynútených vibráciách. Diferenciálna rovnica v prítomnosti viskózneho odporu má tvar: Všeobecné riešenie sa vyberie z tabuľky (3. prednáška, s. 11) v závislosti od pomeru n a k (pozri). Vezmeme konkrétne riešenie v tvare a vypočítame derivácie: Dosadíme v diferenciálnej rovnici: Prirovnaním koeficientov pre identické goniometrické funkcie dostaneme sústavu rovníc: Umocnením oboch rovníc a ich sčítaním dostaneme amplitúdu vynútené kmity: Vydelením druhej rovnice prvou získame fázový posun vynútených kmitov: Pohybová rovnica pre vynútené kmitanie, berúc do úvahy odpor proti pohybu, napríklad pre n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 snímka
5. prednáška Relatívny pohyb hmotného bodu - Predpokladajme, že pohyblivá (neinerciálna) súradnicová sústava Oxyz sa pohybuje podľa nejakého zákona voči pevnej (inerciálnej) súradnicovej sústave O1x1y1z1. Pohyb hmotného bodu M (x, y, z) voči pohyblivej sústave Oxyz je relatívny, voči nehybnej sústave O1x1y1z1 absolútny. Pohyb mobilného systému Oxyz voči pevnému systému O1x1y1z1 je prenosný pohyb. 14 z x1 y1 z1 O1 x y M x y z O Základná rovnica dynamiky: Absolútne zrýchlenie bodu: Do hlavnej rovnice dynamiky dosadíme absolútne zrýchlenie bodu: Prenesme pojmy s translačným a Coriolisovým zrýchlením na pravú stranu: prenesené členy majú rozmer síl a považujú sa za zodpovedajúce zotrvačné sily, rovné: Potom relatívny pohyb bodu môžeme považovať za absolútny, ak k pôsobiacim silám pripočítame translačné a Coriolisove sily zotrvačnosti: V priemetoch na osi pohyblivého súradnicového systému máme: rotácia je rovnomerná, potom εe = 0: 2. Translačný krivočiary pohyb: Ak je pohyb priamočiary, potom = : Ak je pohyb priamočiary a rovnomerný, potom je pohybujúci sa systém zotrvačný a relatívny pohyb možno považovať za absolútny: Žiadne mechanické javy nedokážu rozpoznať priamočiaru uniformu pohybu (princíp relativity klasickej mechaniky). Vplyv rotácie Zeme na rovnováhu telies - Predpokladajme, že teleso je v rovnováhe na zemskom povrchu v ľubovoľnej zemepisnej šírke φ (rovnobežky). Zem sa otáča okolo svojej osi zo západu na východ uhlovou rýchlosťou: Polomer Zeme je asi 6370 km. SR je celková reakcia nehladkého povrchu. G - sila príťažlivosti Zeme do stredu. Ф - odstredivá sila zotrvačnosti. Podmienka relatívnej rovnováhy: Výslednica príťažlivých a zotrvačných síl je gravitačná sila (hmotnosť): Veľkosť gravitačnej sily (hmotnosti) na povrch Zeme je P = mg. Odstredivá sila zotrvačnosti je malým zlomkom gravitačnej sily: Odchýlka gravitačnej sily od smeru príťažlivej sily je tiež malá: Vplyv rotácie Zeme na rovnováhu telies je teda extrémne malý. a neberie sa do úvahy pri praktických výpočtoch. Maximálna hodnota zotrvačnej sily (pri φ = 0 - na rovníku) je len 0,00343 hodnoty gravitácie.

17 snímka
5. prednáška (pokračovanie 5.2) 15 Vplyv rotácie Zeme na pohyb telies v gravitačnom poli Zeme - Predpokladajme, že teleso padá na Zem z určitej výšky H nad povrchom Zeme v zemepisnej šírke φ . Vyberme si pohyblivú vzťažnú sústavu, pevne spojenú so Zemou, smerujúcu osi x, y tangenciálne k rovnobežke a k poludníku: Rovnica relatívneho pohybu: Tu je maličkosť odstredivej sily zotrvačnosti v porovnaní s gravitačnou silou. vziať do úvahy. Gravitačná sila sa teda stotožňuje so silou gravitácie. Okrem toho predpokladáme, že gravitácia je nasmerovaná kolmo na zemský povrch z dôvodu maličkosti jej vychýlenia, ako bolo diskutované vyššie. Coriolisovo zrýchlenie sa rovná a smeruje rovnobežne s osou y na západ. Coriolisova zotrvačná sila smeruje opačným smerom. Rovnicu relatívneho pohybu premietneme na os: Riešenie prvej rovnice dáva: Počiatočné podmienky: Riešenie tretej rovnice dáva: Počiatočné podmienky: Tretia rovnica má tvar: Počiatočné podmienky: Jej riešenie dáva: Výsledné riešenie ukazuje, že teleso sa pri páde odchyľuje na východ. Vypočítajme hodnotu tejto odchýlky napríklad pri páde z výšky 100 m.. Čas pádu zistíme z riešenia druhej rovnice: Vplyv rotácie Zeme na pohyb telies je teda extrémne malý. pre praktické výšky a rýchlosti a v technických výpočtoch sa nezohľadňuje. Z riešenia druhej rovnice vyplýva aj existencia rýchlosti pozdĺž osi y, ktorá by tiež mala spôsobiť a spôsobiť zodpovedajúce zrýchlenie a Coriolisovu zotrvačnú silu. Vplyv tejto rýchlosti a s ňou spojenej zotrvačnej sily na zmenu pohybu bude ešte menší ako uvažovaná Coriolisova zotrvačná sila spojená s vertikálnou rýchlosťou.

18 snímka
6. prednáška Dynamika mechanického systému. Systém hmotných bodov alebo mechanický systém - súbor hmotných bodov alebo tých hmotných bodov spojených všeobecnými zákonmi vzájomného pôsobenia (poloha alebo pohyb každého z bodov alebo tela závisí od polohy a pohybu všetkých ostatných) Systém voľné body - ktorých pohyb nie je obmedzený žiadnymi spojeniami (napríklad planetárny systém, v ktorom sú planéty považované za hmotné body). Systém nevoľných bodov alebo nevoľný mechanický systém - pohyb hmotných bodov alebo telies je obmedzený obmedzeniami kladenými na systém (napríklad mechanizmus, stroj atď.). 16 Sily pôsobiace na systém. Okrem predtým existujúcej klasifikácie síl (činné a reaktívne sily) sa zavádza nová klasifikácia síl: 1. Vonkajšie sily (e) - pôsobiace na body a telesá sústavy z bodov alebo telies, ktoré nie sú jej súčasťou. systém. 2. Vnútorné sily (i) - sily vzájomného pôsobenia medzi hmotnými bodmi alebo telesami zahrnutými v danej sústave. Tá istá sila môže byť vonkajšia aj vnútorná sila. Všetko závisí od toho, ktorý mechanický systém sa zvažuje. Napríklad: V sústave Slnka, Zeme a Mesiaca sú všetky gravitačné sily medzi nimi vnútorné. Pri uvažovaní o sústave Zeme a Mesiaca sú gravitačné sily pôsobiace zo strany Slnka vonkajšie: C Z L Na základe zákona akcie a reakcie každá vnútorná sila Fk zodpovedá inej vnútornej sile Fk', ktorá je rovnaká v absolútnej hodnote a opačná v smer. Z toho vyplývajú dve pozoruhodné vlastnosti vnútorných síl: Hlavný vektor všetkých vnútorných síl sústavy sa rovná nule: Hlavný moment všetkých vnútorných síl sústavy voči ľubovoľnému stredu je rovný nule: Alebo v priemetoch na súradnicu. osi: Pozn. Aj keď sú tieto rovnice podobné rovnovážnym rovniciam, nie sú, pretože vnútorné sily pôsobia na rôzne body alebo telesá systému a môžu spôsobiť, že sa tieto body (telesá) navzájom pohybujú. Z týchto rovníc vyplýva, že vnútorné sily neovplyvňujú pohyb sústavy uvažovanej ako celku. Ťažisko sústavy hmotných bodov. Na opísanie pohybu systému ako celku sa zavedie geometrický bod nazývaný ťažisko, ktorého vektor polomeru je určený výrazom, kde M je hmotnosť celého systému: Alebo v projekciách na súradnicu osi: Vzorce pre ťažisko sú podobné ako pre ťažisko. Pojem ťažisko je však všeobecnejší, pretože nesúvisí s gravitačnými silami alebo gravitačnými silami.

19 snímka
6. prednáška (pokračovanie 6.2) 17 Veta o pohybe ťažiska sústavy - Uvažujme sústavu n hmotných bodov. Sily pôsobiace na každý bod rozdelíme na vonkajšie a vnútorné a nahradíme ich zodpovedajúcimi výslednicami Fke a Fki. Napíšme si pre každý bod základnú rovnicu dynamiky: alebo Sčítajme tieto rovnice cez všetky body: Na ľavej strane rovnice zavedieme hmotnosti pod znamienko derivácie a súčet derivácií nahradíme deriváciou. súčtu: Z definície ťažiska: Do výslednej rovnice dosadíme: dostaneme alebo: Súčin hmotnosti sústavy a zrýchlenia jej ťažiska sa rovná hlavnému vektoru vonkajších síl. Pri projekciách na súradnicové osi: Ťažisko systému sa pohybuje ako hmotný bod s hmotnosťou, rovná hmotnosti celý systém, na ktorý pôsobia všetky vonkajšie sily pôsobiace na systém. Následky z vety o pohybe ťažiska sústavy (zákony zachovania): 1. Ak je v časovom intervale hlavný vektor vonkajších síl sústavy rovný nule, Re = 0, potom rýchlosť ťažisko je konštantné, vC = const (ťažisko sa pohybuje rovnomerne priamočiaro - zákon zachovania ťažiska pohybu). 2. Ak je v časovom intervale priemet hlavného vektora vonkajších síl sústavy na os x rovný nule, Rxe = 0, potom je rýchlosť ťažiska pozdĺž osi x konštantná, vCx = const (ťažisko sa pohybuje rovnomerne pozdĺž osi). Podobné tvrdenia platia pre osi y a z. Príklad: Dvaja ľudia s hmotnosťou m1 a m2 sú na lodi s hmotnosťou m3. V počiatočnom momente bola loď s ľuďmi v kľude. Určte výtlak člna, ak sa osoba s hmotnosťou m2 presunula na provu člna vo vzdialenosti a. 3. Ak je v časovom intervale hlavný vektor vonkajších síl sústavy rovný nule, Re = 0, a v počiatočnom momente je rýchlosť ťažiska nulová, vC = 0, potom je vektor polomeru ťažisko zostáva konštantné, rC = const (ťažisko je v pokoji je zákon zachovania polohy ťažiska). 4. Ak je v časovom intervale priemet hlavného vektora vonkajších síl sústavy na os x rovný nule, Rxe = 0 a v počiatočnom momente je rýchlosť ťažiska pozdĺž tejto osi nulová. , vCx = 0, potom súradnica ťažiska pozdĺž osi x zostáva konštantná, xC = const (ťažisko sa po tejto osi nepohybuje). Podobné tvrdenia platia pre osi y a z. 1. Predmet pohybu (čln s ľuďmi): 2. Zahodíme súvislosti (voda): 3. Spojenie nahradíme reakciou: 4. Sčítame aktívne sily: 5. Napíšte vetu o ťažisku: Premietnite na os x: O Určte, ako ďaleko sa potrebujete presunúť na osobu s hmotnosťou m1, aby loď zostala na mieste: Loď sa posunie o vzdialenosť l opačným smerom.

20 snímka
Prednáška 7 Impulz sily je mierou mechanickej interakcie, ktorá charakterizuje prenos mechanického pohybu zo síl pôsobiacich na bod za daný časový úsek: 18 V projekciách na súradnicové osi: V prípade konštantnej sily: V projekciách na súradnicové osi: do bodu síl v rovnakom časovom intervale: Násobiť dt: Integrovať za daný časový interval: Veľkosť pohybu bodu je mierou mechanického pohybu, určená vektorom rovným súčinu hmotnosť bodu a jeho vektor rýchlosti: Veta o zmene veľkosti pohybu sústavy – Uvažujme sústavu n hmotných bodov. Sily pôsobiace na každý bod rozdelíme na vonkajšie a vnútorné a nahradíme ich zodpovedajúcimi výslednicami Fke a Fki. Napíšme pre každý bod základnú rovnicu dynamiky: alebo Množstvo pohybu sústavy hmotných bodov - geometrický súčet veličín pohybu hmotných bodov: Podľa definície ťažiska: Vektor hybnosti sústavy. sa rovná súčinu hmotnosti celej sústavy a vektora rýchlosti ťažiska sústavy. Potom: Pri projekciách na súradnicové osi: Časová derivácia vektora hybnosti sústavy sa rovná hlavnému vektoru vonkajších síl sústavy. Sčítajme tieto rovnice cez všetky body: Na ľavej strane rovnice zavedieme hmotnosti pod znamienko derivácie a nahradíme súčet derivácií deriváciou súčtu: Z definície hybnosti sústavy: V projekciách na súradnicové osi:

21 snímka
Eulerova veta - Aplikácia vety o zmene hybnosti systému na pohyb spojitého prostredia (vody). 1. Ako objekt pohybu vyberieme objem vody nachádzajúci sa v krivočiarom kanáli turbíny: 2. Spoje zahodíme a ich pôsobenie nahradíme reakciami (Rpov - výslednica povrchových síl) 3. Pridáme aktívne sily (Rb - výslednica síl telesa): 4. Napíšte vetu o zmene hybnosti sústavy: Množstvo pohybu vody v časoch t0 a t1 znázorníme ako súčty: Zmena hybnosti vody v časovom intervale : Zmena hybnosti vody za nekonečne malý časový interval dt: , kde F1 F2 Zo súčinu hustoty, prierezu a rýchlosti za sekundu dostaneme: Dosadením diferenciálu hybnosti sústavy do vety o zmene. , dostaneme: Dôsledky z vety o zmene hybnosti sústavy (zákony zachovania): 1. Ak je v časovom intervale hlavný vektor vonkajších síl sústavy rovný nule, Re = 0, potom pohyb vektora je konštantný, Q = const je zákon zachovania hybnosti sústavy). 2. Ak je v časovom intervale priemet hlavného vektora vonkajších síl sústavy na os x rovný nule, Rxe = 0, potom je priemet hybnosti sústavy na os x konštantný, Qx. = konšt. Podobné tvrdenia platia pre osi y a z. Prednáška 7 (pokračovanie 7.2) Príklad: Granát hmotnosti M letiaci rýchlosťou v sa rozpadol na dve časti. Rýchlosť jedného z úlomkov hmotnosti m1 vzrástla v smere pohybu na hodnotu v1. Určte rýchlosť druhého fragmentu. 1. Predmet pohybu (granát): 2. Predmet je voľný systém, neexistujú žiadne súvislosti a ich reakcie. 3. Pridajte aktívne sily: 4. Napíšte vetu o zmene hybnosti: Premietnite na os: β Oddeľte premenné a integrujte: čas výbuchu t

22 snímka
Prednáška 7 (pokračovanie 7.3) 20 Moment hybnosti bodu alebo kinetický moment pohybu vzhľadom na určitý stred je miera mechanického pohybu, určená vektorom rovným vektorovému súčinu polomerového vektora hmotného bodu a vektor jeho hybnosti: Kinetický moment sústavy hmotných bodov voči určitému stredu je geometrický súčet momentov počtu pohybov všetkých hmotných bodov voči rovnakému stredu: V priemetoch na os: Pri priemetoch na os: Veta o zmene momentu hybnosti sústavy - Uvažujme sústavu n hmotných bodov. Sily pôsobiace na každý bod rozdelíme na vonkajšie a vnútorné a nahradíme ich zodpovedajúcimi výslednicami Fke a Fki. Zapíšme si ku každému bodu základnú rovnicu dynamiky: alebo Sčítajme tieto rovnice pre všetky body: Súčet derivácií nahraďme deriváciou súčtu: Výraz v zátvorkách je moment hybnosti sústavy. Odtiaľto: Každú z rovníc vektorovo vynásobíme polomerovým vektorom vľavo: Pozrime sa, či je možné vziať znamienko derivácie mimo vektorového súčinu: Takto sme dostali: stred. Pri projekciách na súradnicové osi: Derivácia momentu hybnosti systému vzhľadom na niektorú os v čase sa rovná hlavnému momentu vonkajších síl systému vzhľadom na rovnakú os.

23 snímka
Prednáška 8 21 ■ Následky z vety o zmene momentu hybnosti sústavy (zákony zachovania): 1. Ak je v časovom intervale vektor hlavného momentu vonkajších síl sústavy voči určitému stredu rovný na nulu, MOe = 0, potom je vektor momentu hybnosti sústavy voči rovnakému stredu konštantný, KO = const je zákon zachovania hybnosti sústavy). 2. Ak v časovom intervale Hlavným bodom vonkajšie sily sústavy voči osi x sú rovné nule, Mxe = 0, potom je moment hybnosti sústavy voči osi x konštantný, Kx = konšt. Podobné tvrdenia platia pre osi y a z. 2. Moment zotrvačnosti tuhého telesa okolo osi: Moment zotrvačnosti hmotného bodu okolo osi je rovný súčinu hmotnosti bodu a druhej mocniny vzdialenosti bodu od osi. Moment zotrvačnosti tuhého telesa okolo osi sa rovná súčtu súčinov hmotnosti každého bodu a druhej mocniny vzdialenosti tohto bodu od osi. ■ Prvky teórie momentov zotrvačnosti - Pri rotačnom pohybe tuhého telesa je mierou zotrvačnosti (odpor voči zmene pohybu) moment zotrvačnosti okolo osi rotácie. Zvážte základné pojmy definície a metódy výpočtu momentov zotrvačnosti. 1. Moment zotrvačnosti hmotného bodu okolo osi: Pri prechode z diskrétnej malej hmotnosti do nekonečne malej hmotnosti bodu je hranica takéhoto súčtu určená integrálom: osovým momentom zotrvačnosti tuhého telesa. . Okrem osového momentu zotrvačnosti tuhého telesa existujú aj iné druhy momentov zotrvačnosti: odstredivý moment zotrvačnosti tuhého telesa. polárny moment zotrvačnosti tuhého telesa. 3. Veta o momentoch zotrvačnosti tuhého telesa o rovnobežných osiach - vzorec na prechod na rovnobežné osi: Moment zotrvačnosti k referenčnej osi Statické momenty zotrvačnosti k referenčným osám Hmotnosť telesa Vzdialenosť medzi osami z1 a z2 Teda : momenty sú nula:

24 snímka
Prednáška 8 (pokračovanie 8.2) 22 Moment zotrvačnosti rovnomernej tyče konštantného prierezu okolo osi: x z L Vyberte elementárny objem dV = Adx vo vzdialenosti x: x dx Elementárna hmotnosť: Na výpočet momentu zotrvačnosti okolo stredovej osi (pri prechode cez ťažisko), stačí zmeniť umiestnenie osi a nastaviť integračné limity (-L/2, L/2). Tu demonštrujeme vzorec pre prechod na rovnobežné osi: zС 5. Moment zotrvačnosti homogénneho pevného valca okolo osi súmernosti: H dr r Vyčleňme elementárny objem dV = 2πrdrH (tenký valec s polomerom r) : Elementárna hmotnosť: Tu použijeme objemový vzorec valca V=πR2H. Na výpočet momentu zotrvačnosti dutého (hrubého) valca stačí nastaviť integračné limity od R1 do R2 (R2> R1): 6. Moment zotrvačnosti tenkého valca okolo osi symetrie (t

25 snímka
Prednáška 8 (pokračovanie 8.3) 23 ■ Diferenciálna rovnica rotácie tuhého telesa okolo osi: Napíšme vetu o zmene momentu hybnosti tuhého telesa rotujúceho okolo pevnej osi: Hybnosť rotujúceho tuhého telesa je: Moment vonkajších síl okolo osi otáčania sa rovná krútiacemu momentu (reakcie a sila nevytvárajú tiažové momenty): Kinetický moment a krútiaci moment dosadíme do vety Príklad: Dvaja ľudia rovnakej hmotnosti G1 = G2 visia na hodenom lane. cez pevný blok s hmotnosťou G3 = G1/4. V určitom okamihu jeden z nich začal šplhať po lane relatívnou rýchlosťou u. Určite rýchlosť zdvíhania každej osoby. 1. Vyberte objekt pohybu (blok s ľuďmi): 2. Zlikvidujte spojenia (nosné zariadenie bloku): 3. Nahraďte spojenie s reakciami (ložisko): 4. Pridajte aktívne sily (gravitáciu): 5. Zapíšte veta o zmene kinetického momentu sústavy vzhľadom na os otáčania bloku: R Keďže moment vonkajších síl je rovný nule, kinetický moment musí zostať konštantný: V počiatočnom okamihu času t = 0 bol rovnovážny a Kz0 = 0. Po začatí pohybu jednej osoby vzhľadom na lano sa celý systém začal pohybovať, ale kinetický moment systému musí zostať rovný nule: Kz = 0. Moment hybnosti lana sústava je súčet momentov hybnosti ľudí a bloku: Tu v2 je rýchlosť druhej osoby, rovná rýchlosti kábla, Príklad: Určte periódu malých voľných kmitov homogénnej tyče s hmotnosťou M a dĺžka l, zavesená jedným koncom na pevnú os otáčania. Alebo: V prípade malých kmitov sinφ φ: Doba kmitania: Moment zotrvačnosti tyče:

26 snímka
Prednáška 8 (pokračovanie 8.4 - doplnkový materiál) 24 ■ Elementárna teória gyroskopu: Gyroskop je tuhé teleso rotujúce okolo osi súmernosti materiálu, ktorého jeden z bodov je pevný. Voľný gyroskop je upevnený tak, že jeho ťažisko zostáva nehybné a os otáčania prechádza ťažiskom a môže zaujať akúkoľvek polohu v priestore, t.j. os rotácie mení svoju polohu ako os vlastnej rotácie telesa pri sférickom pohybe. Hlavným predpokladom približnej (elementárnej) teórie gyroskopu je, že vektor hybnosti (kinetický moment) rotora sa považuje za smerujúci pozdĺž vlastnej osi rotácie. Napriek tomu, že vo všeobecnosti sa rotor zúčastňuje troch otáčok, berie sa do úvahy iba uhlová rýchlosť jeho vlastnej rotácie ω = dφ/dt. Dôvodom je, že v moderných technológiách sa rotor gyroskopu otáča uhlovou rýchlosťou rádovo 5000-8000 rad/s (asi 50000-80000 ot./min), zatiaľ čo ostatné dve uhlové rýchlosti súvisia s precesiou a nutáciou vlastnej osi. rotácia desaťtisíckrát nižšia ako táto rýchlosť. Hlavnou vlastnosťou voľného gyroskopu je, že os rotora si zachováva rovnaký smer v priestore vzhľadom na inerciálny (hviezdny) referenčný systém (preukázaný Foucaultovým kyvadlom, ktoré udržuje rovinu výkyvu nezmenenú vzhľadom na hviezdy, 1852). Vyplýva to zo zákona zachovania kinetického momentu vzhľadom na ťažisko rotora za predpokladu, že sa zanedbá trenie v ložiskách osí zavesenia rotora, vonkajšieho a vnútorného rámu: Silové pôsobenie na os voľnej gyroskop. V prípade sily pôsobiacej na os rotora sa moment vonkajších síl vzhľadom na ťažisko nerovná nule: ω ω С sila, a smerom k vektoru momentu tejto sily, t.j. sa bude otáčať nie okolo osi x (vnútorné zavesenie), ale okolo osi y (vonkajšie zavesenie). Po ukončení pôsobenia sily zostane os rotora v rovnakej polohe, ktorá zodpovedá poslednému času pôsobenia sily, pretože od tohto okamihu sa moment vonkajších síl opäť rovná nule. Pri krátkodobom pôsobení sily (nárazu) os gyroskopu prakticky nemení svoju polohu. Rýchla rotácia rotora teda dáva gyroskopu schopnosť pôsobiť proti náhodným vplyvom, ktoré sa snažia zmeniť polohu osi rotácie rotora a pri konštantnom pôsobení sily udržiava polohu roviny kolmej na pôsobiaca sila, v ktorej leží os rotora. Tieto vlastnosti sa využívajú pri prevádzke inerciálnych navigačných systémov.
Ako súčasť každého učebného plánu sa štúdium fyziky začína mechanikou. Nie z teoretickej, nie z aplikovanej a nie výpočtovej, ale zo starej dobrej klasickej mechaniky. Táto mechanika sa nazýva aj newtonovská mechanika. Podľa legendy sa vedec prechádzal po záhrade, videl padať jablko a práve tento jav ho podnietil objaviť zákon univerzálnej gravitácie. Samozrejme, zákon vždy existoval a Newton mu dal len formu zrozumiteľnú pre ľudí, no jeho zásluha je na nezaplatenie. V tomto článku nebudeme čo najpodrobnejšie popisovať zákony newtonovskej mechaniky, ale načrtneme základy, základné poznatky, definície a vzorce, ktoré vám vždy môžu hrať do karát.
Mechanika je odvetvie fyziky, veda, ktorá študuje pohyb hmotných telies a interakcie medzi nimi.
Samotné slovo má grécky pôvod a prekladá sa ako „umenie stavať stroje“. Pred stavbou strojov nás však čaká ešte dlhá cesta, poďme teda po stopách našich predkov a budeme študovať pohyb kameňov vrhaných šikmo k horizontu a padajúcich jabĺk na hlavy z výšky h.

Prečo sa štúdium fyziky začína mechanikou? Pretože je úplne prirodzené nevychádzať z termodynamickej rovnováhy?!
Mechanika je jednou z najstarších vied a historicky sa štúdium fyziky začalo práve základmi mechaniky. Ľudia umiestnení v rámci času a priestoru v skutočnosti nemohli začať od niečoho iného, bez ohľadu na to, ako veľmi chceli. Pohybujúce sa telá sú to prvé, čomu venujeme pozornosť.
čo je pohyb?
Mechanický pohyb je zmena polohy telies v priestore voči sebe v priebehu času.
Po tejto definícii sa celkom prirodzene dostávame k pojmu referenčný rámec. Zmena polohy telies v priestore voči sebe navzájom. Kľúčové slová tu: voči sebe navzájom . Koniec koncov, cestujúci v aute sa pohybuje vo vzťahu k osobe stojacej na kraji cesty určitou rýchlosťou a spočíva vo vzťahu k svojmu susedovi na neďalekom sedadle a pohybuje sa inou rýchlosťou vo vzťahu k cestujúcemu v aute, ktoré ich predbehne.

To je dôvod, prečo, aby sme normálne zmerali parametre pohybujúcich sa objektov a nezamenili sa, potrebujeme referenčný systém - pevne prepojené referenčné teleso, súradnicový systém a hodiny. Napríklad Zem sa pohybuje okolo Slnka v heliocentrickej referenčnej sústave. V každodennom živote takmer všetky merania realizujeme v geocentrickom referenčnom systéme spojenom so Zemou. Zem je referenčné teleso, voči ktorému sa pohybujú autá, lietadlá, ľudia, zvieratá.

Mechanika ako veda má svoju vlastnú úlohu. Úlohou mechanikov je kedykoľvek poznať polohu telesa v priestore. Inými slovami, mechanika konštruuje matematický popis pohybu a nachádza súvislosti medzi fyzikálnymi veličinami, ktoré ho charakterizujú.
Aby sme sa mohli posunúť ďalej, potrebujeme pojem „ hmotný bod ". Hovorí sa, že fyzika je presná veda, ale fyzici vedia, koľko aproximácií a predpokladov treba urobiť, aby sa zhodli práve na tejto presnosti. Nikto nikdy nevidel hmotný bod ani nenačuchal ideálny plyn, ale existujú! Len sa s nimi žije oveľa ľahšie.
Hmotný bod je teleso, ktorého veľkosť a tvar možno v kontexte tohto problému zanedbať.
Časti klasickej mechaniky
Mechanika pozostáva z niekoľkých sekcií
- Kinematika
- Dynamika
- Statika
Kinematika S fyzický bod zrak študuje, ako sa telo pohybuje. Inými slovami, táto časť sa zaoberá kvantitatívnymi charakteristikami pohybu. Nájsť rýchlosť, dráhu – typické úlohy kinematiky
Dynamika rieši otázku, prečo sa pohybuje tak, ako sa pohybuje. To znamená, že berie do úvahy sily pôsobiace na telo.
Statikaštuduje rovnováhu telies pri pôsobení síl, čiže odpovedá na otázku: prečo vôbec nepadá?
Hranice použiteľnosti klasickej mechaniky
Klasická mechanika už netvrdí, že je vedou, ktorá všetko vysvetľuje (začiatkom minulého storočia bolo všetko úplne inak) a má jasný rozsah pôsobnosti. Vo všeobecnosti sú zákony klasickej mechaniky platné pre svet známy z hľadiska veľkosti (makrosvet). Prestávajú fungovať v prípade sveta častíc, keď klasickú mechaniku nahrádza kvantová mechanika. Klasická mechanika je tiež nepoužiteľná v prípadoch, keď k pohybu telies dochádza rýchlosťou blízkou rýchlosti svetla. V takýchto prípadoch sa prejavia relativistické efekty. Zhruba povedané, v rámci kvantovej a relativistickej mechaniky – klasickej mechaniky ide o špeciálny prípad, keď sú rozmery telesa veľké a rýchlosť malá.

Všeobecne povedané, kvantové a relativistické efekty nikdy nezmiznú, prebiehajú aj pri bežnom pohybe makroskopických telies rýchlosťou oveľa nižšou ako je rýchlosť svetla. Ďalšia vec je, že pôsobenie týchto efektov je také malé, že nepresahuje najpresnejšie merania. Klasická mechanika tak nikdy nestratí svoj základný význam.
V štúdiu fyzikálnych základov mechaniky budeme pokračovať v budúcich článkoch. Pre lepšie pochopenie mechaniky sa vždy môžete odvolať našich autorov, ktoré jednotlivo vrhajú svetlo na temný bod najťažšej úlohy.
Teoretická mechanika- Ide o odvetvie mechaniky, ktoré stanovuje základné zákony mechanického pohybu a mechanickej interakcie hmotných telies.
Teoretická mechanika je veda, v ktorej sa skúmajú pohyby telies v čase (mechanické pohyby). Slúži ako základ pre ďalšie sekcie mechaniky (teória pružnosti, odolnosti materiálov, teória plasticity, teória mechanizmov a strojov, hydroaerodynamika) a mnohé technické disciplíny.
mechanický pohyb- ide o časovú zmenu relatívnej polohy v priestore hmotných telies.
Mechanická interakcia- je to taká interakcia, v dôsledku ktorej sa mení mechanický pohyb alebo sa mení vzájomná poloha častí tela.
Pevná statika tela
Statika- Ide o odvetvie teoretickej mechaniky, ktoré sa zaoberá problémami rovnováhy pevných telies a premenou jedného systému síl na iný, jemu ekvivalentný.
- Základné pojmy a zákony statiky
- Absolútne tuhé telo(pevné teleso, teleso) je hmotné teleso, vzdialenosť medzi akýmikoľvek bodmi sa nemení.
- Materiálny bod je teleso, ktorého rozmery podľa podmienok problému možno zanedbať.
- uvoľnené telo je teleso, na pohyb ktorého nie sú kladené žiadne obmedzenia.
- Nevoľné (viazané) telo je teleso, ktorého pohyb je obmedzený.
- Spojenia- sú to telesá, ktoré bránia pohybu uvažovaného objektu (telesa alebo sústavy telies).
- Komunikačná reakcia je sila, ktorá charakterizuje pôsobenie väzby na tuhé teleso. Ak silu, ktorou tuhé teleso pôsobí na väzbu, považujeme za akciu, potom je reakcia väzby protiakciou. V tomto prípade sa sila - pôsobenie aplikuje na spojenie a reakcia spojenia sa aplikuje na pevné teleso.
- mechanický systém je súbor vzájomne prepojených telies alebo hmotných bodov.
- Pevné možno považovať za mechanický systém, ktorého polohy a vzdialenosť medzi bodmi sa nemenia.
- Pevnosť je vektorová veličina charakterizujúca mechanické pôsobenie jedného hmotného telesa na druhé.
Sila ako vektor je charakterizovaná bodom pôsobenia, smerom pôsobenia a absolútnou hodnotou. Jednotkou merania modulu sily je Newton. - siločiara je priamka, pozdĺž ktorej smeruje vektor sily.
- Koncentrovaná sila je sila pôsobiaca v jednom bode.
- Rozložené sily (rozložené zaťaženie)- sú to sily pôsobiace na všetky body objemu, povrchu alebo dĺžky telesa.
Rozložené zaťaženie je dané silou pôsobiacou na jednotku objemu (plocha, dĺžka).
Rozmer rozloženého zaťaženia je N / m 3 (N / m 2, N / m). - Vonkajšia sila je sila pôsobiaca od telesa, ktorá nepatrí do uvažovaného mechanického systému.
- vnútorná sila je sila pôsobiaca na hmotný bod mechanického systému z iného hmotného bodu prislúchajúceho do posudzovaného systému.
- Silový systém je súhrn síl pôsobiacich na mechanický systém.
- Plochý systém síl je sústava síl, ktorých akčné línie ležia v rovnakej rovine.
- Priestorový systém síl je sústava síl, ktorých akčné línie neležia v rovnakej rovine.
- Systém konvergujúcich síl je sústava síl, ktorých akčné línie sa pretínajú v jednom bode.
- Svojvoľný systém síl je sústava síl, ktorých akčné línie sa nepretínajú v jednom bode.
- Ekvivalentné sústavy síl- sú to sústavy síl, ktorých výmena jedna za druhú nemení mechanický stav tela.
Akceptované označenie: . - Rovnováha Stav, v ktorom teleso pôsobením síl zostáva nehybné alebo sa pohybuje rovnomerne v priamom smere.
- Vyvážený systém síl- ide o sústavu síl, ktorá pri pôsobení na voľné pevné teleso nemení jeho mechanický stav (nevyvádza ho z rovnováhy).
 .
. - výsledná sila je sila, ktorej pôsobenie na teleso je ekvivalentné pôsobeniu sústavy síl.
 .
. - Moment sily je hodnota, ktorá charakterizuje rotačnú schopnosť sily.
- Mocenský pár je systém dvoch rovnobežných, v absolútnej hodnote rovnakých, opačne smerujúcich síl.
Akceptované označenie: .
Pôsobením niekoľkých síl telo vykoná rotačný pohyb. - Projekcia sily na osi- je to úsečka uzavretá medzi kolmicami vedenými od začiatku a konca vektora sily k tejto osi.
Projekcia je kladná, ak sa smer segmentu zhoduje s kladným smerom osi. - Projekcia sily na rovine je vektor v rovine uzavretej medzi kolmicami vedenými od začiatku a konca vektora sily k tejto rovine.
- Zákon 1 (zákon zotrvačnosti). Izolovaný hmotný bod je v pokoji alebo sa pohybuje rovnomerne a priamočiaro.
Rovnomerný a priamočiary pohyb hmotného bodu je pohyb zotrvačnosťou. Rovnovážny stav hmotného bodu a tuhého telesa sa chápe nielen ako stav pokoja, ale aj ako pohyb zotrvačnosťou. Pre tuhé teleso existujú rôzne typy zotrvačného pohybu, napríklad rovnomerné otáčanie tuhého telesa okolo pevnej osi. - Zákon 2. Pevné teleso je v rovnováhe pri pôsobení dvoch síl iba vtedy, ak sú tieto sily rovnako veľké a smerované v opačných smeroch pozdĺž spoločnej akčnej línie.
Tieto dve sily sa nazývajú vyvážené.
Vo všeobecnosti sa sily považujú za vyrovnané, ak je tuhé teleso, na ktoré tieto sily pôsobia, v pokoji. - Zákon 3. Bez narušenia stavu (slovo „stav“ tu znamená stav pohybu alebo pokoja) tuhého telesa je možné pridávať a odstraňovať vyrovnávacie sily.
Dôsledok. Bez narušenia stavu tuhého telesa môže byť sila prenesená pozdĺž svojej akčnej línie do akéhokoľvek bodu telesa.
Dva systémy síl sa nazývajú ekvivalentné, ak jeden z nich môže byť nahradený iným bez narušenia stavu tuhého telesa. - Zákon 4. Výslednica dvoch síl pôsobiacich v jednom bode pôsobí v tom istom bode, v absolútnej hodnote sa rovná uhlopriečke rovnobežníka postaveného na týchto silách a smeruje pozdĺž tohto
uhlopriečky.
Modul výsledku je: - Zákon 5 (zákon o rovnosti akcie a reakcie). Sily, ktorými na seba dve telesá pôsobia, sú rovnako veľké a smerujú v opačných smeroch pozdĺž jednej priamky.
Treba mať na pamäti, že akcie- sila pôsobiaca na telo B a opozície- sila pôsobiaca na telo ALE, nie sú vyvážené, pretože sú pripojené k rôznym telám. - Zákon 6 (zákon otužovania). Pri tuhnutí nie je narušená rovnováha nepevného telesa.
Netreba zabúdať, že rovnovážne podmienky, ktoré sú nevyhnutné a postačujúce pre tuhé teleso, sú nevyhnutné, ale nedostatočné pre zodpovedajúce netuhé teleso. - Zákon 7 (zákon o uvoľnení z dlhopisov). Nevoľné pevné teleso možno považovať za slobodné, ak je duševne oslobodené od väzieb, pričom pôsobenie väzieb nahrádza zodpovedajúcimi reakciami väzieb.
- Spojenia a ich reakcie
- Jemný povrch obmedzuje pohyb pozdĺž normály k nosnej ploche. Reakcia smeruje kolmo k povrchu.
- Kĺbová pohyblivá podpera obmedzuje pohyb tela pozdĺž normály k referenčnej rovine. Reakcia smeruje pozdĺž normály k povrchu nosiča.
- Kĺbová pevná podpera pôsobí proti akémukoľvek pohybu v rovine kolmej na os otáčania.
- Kĺbový beztiažový prút pôsobí proti pohybu tela pozdĺž línie tyče. Reakcia bude smerovať pozdĺž línie tyče.
- Slepé ukončenie pôsobí proti akémukoľvek pohybu a rotácii v rovine. Jeho pôsobenie môže byť nahradené silou prezentovanou vo forme dvoch zložiek a dvojice síl s momentom.




Kinematika
Kinematika- oddiel teoretickej mechaniky, ktorý uvažuje o všeobecných geometrických vlastnostiach mechanického pohybu, ako procesu prebiehajúceho v priestore a čase. Pohybujúce sa objekty sa považujú za geometrické body alebo geometrické telesá.
- Základné pojmy kinematiky
- Zákon pohybu bodu (telesa) je závislosť polohy bodu (telesa) v priestore od času.
- Bodová trajektória je ťažisko polôh bodu v priestore počas jeho pohybu.
- Bodová (telesná) rýchlosť- ide o charakteristiku zmeny polohy bodu (telesa) v priestore v čase.
- Bodové (telesné) zrýchlenie- ide o charakteristiku časovej zmeny rýchlosti bodu (telesa).
- Určenie kinematických charakteristík bodu
- Bodová trajektória
Vo vektorovom referenčnom systéme je trajektória opísaná výrazom: .
V súradnicovom referenčnom systéme je dráha určená podľa zákona o pohybe bodu a je opísaná výrazmi z = f(x,y) vo vesmíre, príp y = f(x)- v lietadle.
V prirodzenom referenčnom systéme je trajektória vopred určená. - Určenie rýchlosti bodu vo vektorovom súradnicovom systéme
Pri špecifikácii pohybu bodu vo vektorovom súradnicovom systéme sa pomer pohybu k časovému intervalu nazýva priemerná hodnota rýchlosti v tomto časovom intervale: .
Ak vezmeme časový interval ako nekonečne malú hodnotu, dostaneme hodnotu rýchlosti v danom čase (okamžitú hodnotu rýchlosti): .
.
Vektor priemernej rýchlosti smeruje pozdĺž vektora v smere pohybu bodu, vektor okamžitej rýchlosti smeruje tangenciálne k trajektórii v smere pohybu bodu.
záver: rýchlosť bodu je vektorová veličina rovnajúca sa derivácii pohybového zákona vzhľadom na čas.
Odvodená vlastnosť: časová derivácia akejkoľvek hodnoty určuje rýchlosť zmeny tejto hodnoty. - Určenie rýchlosti bodu v súradnicovom referenčnom systéme
Rýchlosť zmeny súradníc bodu: .
.
Modul plnej rýchlosti bodu s pravouhlým súradnicovým systémom sa bude rovnať: .
.
Smer vektora rýchlosti je určený kosínusom uhlov riadenia: ,
,
kde sú uhly medzi vektorom rýchlosti a súradnicovými osami. - Určenie rýchlosti bodu v prirodzenom referenčnom systéme
Rýchlosť bodu v prirodzenom referenčnom systéme je definovaná ako derivácia zákona o pohybe bodu: .
Podľa predchádzajúcich záverov vektor rýchlosti smeruje tangenciálne k trajektórii v smere pohybu bodu a v osiach je určený iba jednou projekciou .
- Kinematika tuhého tela
- V kinematike tuhých telies sa riešia dva hlavné problémy:
1) úloha pohybu a určenie kinematických charakteristík tela ako celku;
2) určenie kinematických charakteristík bodov telesa. - Translačný pohyb tuhého telesa
Translačný pohyb je pohyb, pri ktorom priamka vedená dvoma bodmi tela zostáva rovnobežná s jeho pôvodnou polohou.
Veta: pri translačnom pohybe sa všetky body telesa pohybujú po rovnakých trajektóriách a v každom časovom okamihu majú rovnakú rýchlosť a zrýchlenie vo veľkosti a smere.
záver: translačný pohyb tuhého telesa je určený pohybom ktoréhokoľvek z jeho bodov, a preto je úloha a štúdium jeho pohybu redukované na kinematiku bodu.. - Rotačný pohyb tuhého telesa okolo pevnej osi
Rotačný pohyb tuhého telesa okolo pevnej osi je pohyb tuhého telesa, pri ktorom dva body patriace telesu zostávajú nehybné počas celej doby pohybu.
Poloha tela je určená uhlom natočenia. Jednotkou merania uhla sú radiány. (Radián je stredový uhol kruhu, ktorého dĺžka oblúka sa rovná polomeru, celý uhol kruhu obsahuje 2π radián.)
Zákon rotačného pohybu telesa okolo pevnej osi.
Uhlová rýchlosť a uhlové zrýchlenie telesa budú určené metódou diferenciácie:
— uhlová rýchlosť, rad/s;
— uhlové zrýchlenie, rad/s².
Ak teleso prerežeme o rovinu kolmú na os, zvolíme bod na osi rotácie OD a ľubovoľný bod M, potom bod M bude popisovať okolo bodu OD polomerový kruh R. Počas dt existuje elementárna rotácia cez uhol , zatiaľ čo bod M sa bude pohybovať pozdĺž trajektórie na určitú vzdialenosť .
.
Modul lineárnej rýchlosti: .
.
bodové zrýchlenie M so známou trajektóriou je určená jej komponentmi: ,
,
kde .
.
V dôsledku toho dostaneme vzorce
tangenciálne zrýchlenie: ;
;
normálne zrýchlenie: .
.

Dynamika
Dynamika- Ide o odvetvie teoretickej mechaniky, ktoré študuje mechanické pohyby hmotných telies v závislosti od príčin, ktoré ich spôsobujú.
- Základné pojmy dynamiky
- zotrvačnosť- ide o vlastnosť hmotných telies udržiavať stav pokoja alebo rovnomerného priamočiareho pohybu, kým vonkajšie sily tento stav nezmenia.
- Hmotnosť je kvantitatívna miera zotrvačnosti telesa. Jednotkou hmotnosti je kilogram (kg).
- Materiálny bod je teleso s hmotnosťou, ktorej rozmery sa pri riešení tohto problému zanedbávajú.
- Ťažisko mechanického systému je geometrický bod, ktorého súradnice sú určené vzorcami:
kde m k, x k, y k, z k- hmotnosť a súradnice k- ten bod mechanického systému, m je hmotnosť systému.
V rovnomernom ťažisku sa poloha ťažiska zhoduje s polohou ťažiska. - Moment zotrvačnosti hmotného telesa okolo osi je kvantitatívna miera zotrvačnosti počas rotačného pohybu.
Moment zotrvačnosti hmotného bodu okolo osi sa rovná súčinu hmotnosti bodu a druhej mocniny vzdialenosti bodu od osi: .
.
Moment zotrvačnosti sústavy (telesa) okolo osi sa rovná aritmetickému súčtu momentov zotrvačnosti všetkých bodov:
- Zotrvačná sila hmotného bodu je vektorová veličina, ktorá sa v absolútnej hodnote rovná súčinu hmotnosti bodu a modulu zrýchlenia a smeruje opačne k vektoru zrýchlenia:
- Zotrvačná sila hmotného telesa je vektorová veličina, ktorá sa v absolútnej hodnote rovná súčinu hmotnosti tela a modulu zrýchlenia ťažiska telesa a smeruje opačne k vektoru zrýchlenia ťažiska: ,
kde je zrýchlenie ťažiska telesa. - Impulz elementárnej sily je vektorová veličina rovnajúca sa súčinu vektora sily o nekonečne malý časový interval dt:
.
Celkový impulz sily pre Δt sa rovná integrálu základných impulzov: .
. - Elementárna sila je skalár dA, rovný skalárnemu
Vyhliadka: Tento článok bol čítaný 32852 krát
Pdf Vyberte jazyk... Ruština Ukrajinčina Angličtina
Krátka recenzia
Úplný materiál sa stiahne vyššie po výbere jazyka
- Statika
- Základné pojmy statiky
- Silové typy
- Axiómy statiky
- Spojenia a ich reakcie
- Systém konvergujúcich síl
- Metódy na určenie výsledného systému zbiehajúcich sa síl
- Podmienky rovnováhy pre sústavu konvergujúcich síl
- Moment sily okolo stredu ako vektor
- Algebraická hodnota momentu sily
- Vlastnosti momentu sily okolo stredu (bodu)
- Teória dvojíc síl
- Sčítanie dvoch paralelných síl v rovnakom smere
- Sčítanie dvoch paralelných síl smerujúcich v opačných smeroch
- Výkonové páry
- Vety o páre síl
- Podmienky pre rovnováhu sústavy dvojíc síl
- Rameno páky
- Ľubovoľný rovinný systém síl
- Prípady zníženia plochého systému síl na viac obyčajný pohľad
- Podmienky analytickej rovnováhy
- Stred paralelných síl. Ťažisko
- Stred paralelných síl
- Ťažisko tuhého telesa a jeho súradnice
- Ťažisko objemu, roviny a priamky
- Metódy určenia polohy ťažiska
- Základy silových pretekov
- Problémy a metódy odolnosti materiálov
- Klasifikácia zaťaženia
- Klasifikácia konštrukčných prvkov
- Deformácie tyče
- Hlavné hypotézy a princípy
- Vnútorné sily. Sekčná metóda
- Napätie
- Napätie a kompresia
- Mechanické vlastnosti materiálu
- Prípustné napätia
- Tvrdosť materiálu
- Grafy pozdĺžnych síl a napätí
- Shift
- Geometrické charakteristiky rezov
- Krútenie
- ohnúť
- Diferenciálne závislosti v ohybe
- Ohybová pevnosť
- normálne stresy. Výpočet pevnosti
- Šmykové napätia pri ohybe
- Tuhosť v ohybe
- Prvky všeobecnej teórie napätosti
- Teórie sily
- Ohýbanie s krútením
- Kinematika
- Bodová kinematika
- Bodová trajektória
- Metódy na určenie pohybu bodu
- Bodová rýchlosť
- bodové zrýchlenie
- Kinematika tuhého tela
- Translačný pohyb tuhého telesa
- Rotačný pohyb tuhého telesa
- Kinematika prevodových mechanizmov
- Rovinnoparalelný pohyb tuhého telesa
- Komplexný pohyb bodu
- Bodová kinematika
- Dynamika
- Základné zákony dynamiky
- Bodová dynamika
- Diferenciálne rovnice voľného hmotného bodu
- Dva problémy bodovej dynamiky
- Dynamika tuhého tela
- Klasifikácia síl pôsobiacich na mechanickú sústavu
- Diferenciálne pohybové rovnice mechanického systému
- Všeobecné teorémy dynamiky
- Veta o pohybe ťažiska mechanického systému
- Veta o zmene hybnosti
- Veta o zmene momentu hybnosti
- Veta o zmene kinetickej energie
- Sily pôsobiace v strojoch
- Sily v zábere čelného ozubeného kolesa
- Trenie v mechanizmoch a strojoch
- Klzné trenie
- valivé trenie
- Efektívnosť
- Časti strojov
- Mechanické prevodovky
- Druhy mechanických prevodov
- Základné a odvodené parametre mechanických prevodov
- ozubené kolesá
- Ozubené kolesá s flexibilnými spojmi
- Hriadele
- Účel a klasifikácia
- Návrhový výpočet
- Skontrolujte výpočet hriadeľov
- Ložiská
- Klzné ložiská
- Valivé ložiská
- Spojenie častí stroja
- Typy odpojiteľných a trvalých spojení
- Kľúčové spojenia
- Mechanické prevodovky
- Štandardizácia noriem, zameniteľnosť
- Tolerancie a pristátia
- Jednotný systém tolerancií a pristátí (ESDP)
- Odchýlka tvaru a polohy
Formát: pdf
Veľkosť: 4 MB
ruský jazyk
Príklad výpočtu čelného ozubeného kolesa
Príklad výpočtu čelného ozubeného kolesa. Uskutočnil sa výber materiálu, výpočet dovolených napätí, výpočet dotykovej a ohybovej pevnosti.
Príklad riešenia problému ohýbania lúča
V príklade sú vykreslené diagramy priečnych síl a ohybových momentov, nájde sa nebezpečný úsek a vyberie sa I-nosník. V úlohe bola analyzovaná konštrukcia diagramov pomocou diferenciálnych závislostí, bola vykonaná porovnávacia analýza rôznych prierezov nosníkov.
Príklad riešenia problému krútenia hriadeľa
Úlohou je otestovať pevnosť oceľového hriadeľa pre daný priemer, materiál a dovolené napätia. Pri riešení sa zostavujú diagramy krútiacich momentov, šmykových napätí a uhlov skrútenia. Vlastná hmotnosť hriadeľa sa neberie do úvahy
Príklad riešenia problému ťah-stlačenie tyče
Úlohou je otestovať pevnosť oceľovej tyče pri daných dovolených napätiach. Pri riešení sa zostavujú grafy pozdĺžnych síl, normálových napätí a posunov. Vlastná hmotnosť tyče sa neberie do úvahy
Aplikácia vety o zachovaní kinetickej energie
Príklad riešenia úlohy aplikácie vety o zachovaní kinetickej energie mechanického systému
Určenie rýchlosti a zrýchlenia bodu podľa daných pohybových rovníc
Príklad riešenia úlohy určenia rýchlosti a zrýchlenia bodu podľa daných pohybových rovníc
Určovanie rýchlostí a zrýchlení bodov tuhého telesa pri planparalelnom pohybe
Príklad riešenia úlohy určenia rýchlostí a zrýchlení bodov tuhého telesa pri rovinnoparalelnom pohybe
Stanovenie síl v rovinných priehradových prútoch
Príklad riešenia problému určenia síl v prútoch plochého krovu Ritterovou metódou a metódou rezania uzlov
štátna autonómna inštitúcia
Kaliningradská oblasť
profesijná vzdelávacia organizácia
Vysoká škola služieb a cestovného ruchu
Priebeh prednášok s ukážkami praktických úloh
"Základy teoretickej mechaniky"
disciplínouTechnická mechanika
pre študentov3 kurz
špeciality20.02.04 Požiarna bezpečnosť
Kaliningrad
SCHVÁLIŤ
Zástupca riaditeľa pre SD GAU KO VEO KSTN.N. Myasnikov
SCHVÁLENÉ
Metodická rada GAU KO VET KST
UVAŽOVANÉ
Na zasadnutí PCC
Redakčný tím:
Kolganova A.A., metodička
Falaleeva A.B., učiteľka ruského jazyka a literatúry
Cvetaeva L.V., predseda PCCvšeobecné matematické a prírodovedné disciplíny
Skomplikovaný:
Nezvanová I.V. Lektor GAU KO VET KST
Obsah
Teoretické informácie
Teoretické informácie
Príklady riešenia praktických problémov
Dynamika: základné pojmy a axiómy
Teoretické informácie
Príklady riešenia praktických problémov
Bibliografia
Teoretické informácie
Statika: základné pojmy a axiómy.
Statika - časť teoretickej mechaniky, ktorá sa zaoberá vlastnosťami síl pôsobiacich na body tuhého telesa a podmienkami ich rovnováhy. Hlavné ciele:
1. Transformácia sústav síl na ekvivalentné sústavy síl.
2. Určenie podmienok pre rovnováhu sústav síl pôsobiacich na tuhé teleso.
hmotný bod nazývaný najjednoduchší model hmotného telesa
akýkoľvek tvar, ktorého rozmery sú dostatočne malé a ktorý možno považovať za geometrický bod s určitou hmotnosťou. Mechanický systém je akýkoľvek súbor hmotných bodov. Absolútne tuhé telo je mechanický systém, ktorého vzdialenosti medzi bodmi sa pri žiadnych interakciách nemenia.
Pevnosť je mierou mechanickej interakcie hmotných telies navzájom. Sila je vektorová veličina, pretože je určená tromi prvkami:
číselná hodnota;
smer;
bod aplikácie (A).
Jednotkou sily je Newton (N).

Obrázok 1.1
Systém síl je súbor síl pôsobiacich na teleso.
Vyvážený (rovnajúci sa nule) systém síl je systém, ktorý pri aplikácii na teleso nemení svoj stav.
Sústavu síl pôsobiacich na teleso možno nahradiť jednou výslednicou pôsobiacou ako sústava síl.
Axiómy statiky.
axióma 1: Ak na teleso pôsobí vyvážený systém síl, potom sa pohybuje rovnomerne a priamočiaro alebo je v pokoji (zákon zotrvačnosti).
axióma 2:
Absolútne tuhé teleso je v rovnováhe pri pôsobení dvoch síl vtedy a len vtedy, ak sú tieto sily rovnaké v absolútnej hodnote, pôsobia v jednej priamke a sú nasmerované v opačných smeroch. Obrázok 1.2
axióma 3:
Mechanický stav telesa sa nenaruší, ak sa k sústave síl, ktoré naň pôsobia, pridá alebo uberie vyvážený systém síl.
axióma 4: Výslednica dvoch síl pôsobiacich na teleso sa rovná ich geometrickému súčtu, to znamená, že je vyjadrená v absolútnej hodnote a smere uhlopriečkou rovnobežníka postaveného na týchto silách ako na stranách.
Obrázok 1.3.
axióma 5:
Sily, ktorými na seba dve telesá pôsobia, sú vždy rovnaké v absolútnej hodnote a smerujú pozdĺž jednej priamky v opačných smeroch.
Obrázok 1.4.
Typy väzieb a ich reakcie
spojenia
sa nazývajú akékoľvek obmedzenia, ktoré bránia pohybu tela v priestore. Teleso, ktoré sa pôsobením pôsobiacich síl snaží pohnúť, čomu bráni spojenie, bude naň pôsobiť určitou silou tzv. sila tlaku na spoj
. Podľa zákona o rovnosti akcie a reakcie bude spojenie pôsobiť na teleso rovnakým modulom, ale opačne smerujúcou silou.
Sila, s ktorou toto spojenie pôsobí na telo a bráni jednému alebo druhému pohybu, sa nazýva reakčná sila (reakcia) väzby
.
Jedným zo základných princípov mechaniky je princíp oslobodenia
:
akékoľvek nevoľné teleso možno považovať za voľné, ak väzby zahodíme a ich pôsobenie nahradíme reakciami väzieb.
Väzbová reakcia smeruje opačným smerom, ako väzba neumožňuje pohyb tela. Hlavné typy väzieb a ich reakcie sú uvedené v tabuľke 1.1.
Tabuľka 1.1
Typy väzieb a ich reakcie
Názov komunikácie
1
Hladký povrch (podpora)
- plocha (opora), trenie, o ktoré možno dané teleso zanedbať.
S bezplatnou podporou, reakciasmeruje kolmo na dotyčnicu cez bodALE
telesný kontakt1
s nosnou plochou2
.

2
Závit (flexibilný, neroztiahnuteľný). Spojenie, vytvorené vo forme neroztiahnuteľného vlákna, neumožňuje telesu vzdialiť sa od bodu zavesenia. Preto je reakcia nite smerovaná pozdĺž nite až do bodu jej zavesenia.

3
beztiažový prút
– prút, ktorého hmotnosť možno zanedbať v porovnaní s vnímaným zaťažením.
Reakcia beztiažovej sklopnej priamočiarej tyče smeruje pozdĺž osi tyče.

4
Pohyblivý pánt, kĺbová pohyblivá podpera. Reakcia smeruje pozdĺž normály k nosnému povrchu.

7
Pevný uzáver.
V rovine tuhého uloženia budú dve zložky reakcie,
a moment dvojice síl, ktorý zabraňuje otáčaniu lúča1
vzhľadom na bodALE
.
Pevné uchytenie v priestore odoberá telesu 1 všetkých šesť stupňov voľnosti - tri posunutia pozdĺž súradnicových osí a tri rotácie okolo týchto osí.
V priestorovom tuhom uložení budú tri komponenty,
,
a tri momenty párov síl![]() .
.

Systém konvergujúcich síl
Systém konvergujúcich síl
nazývaný systém síl, ktorých akčné línie sa pretínajú v jednom bode. Dve sily zbiehajúce sa v jednom bode môžu byť podľa tretej axiómy statiky nahradené jednou silou -výsledný
.
Hlavný vektor sústavy síl
- hodnota rovnajúca sa geometrickému súčtu síl sústavy.
Výslednica rovinnej sústavy zbiehajúcich sa síl možno definovaťgraficky a analyticky.
Sčítanie sústavy síl . Sčítanie plochej sústavy zbiehajúcich sa síl sa uskutočňuje buď postupným sčítaním síl s konštrukciou medzivýslednice (obr. 1.5), alebo zostrojením silového mnohouholníka (obr. 1.6).


Obrázok 1.5Obrázok 1.6
Projekcia sily na osi
- algebraická veličina rovnajúca sa súčinu modulu sily a kosínusu uhla medzi silou a kladným smerom osi.
ProjekciaFX(obr.1.7) sily na nápravu Xkladné, ak je α akútne, záporné, ak je α tupé. Ak silaje kolmá na os, potom je jej priemet na os nulový.

Obrázok 1.7
Projekcia sily na rovine Oh– vektor , uzavretý medzi projekciami začiatku a konca silydo tejto roviny. Tie. priemet sily do roviny je vektorová veličina charakterizovaná nielen číselnou hodnotou, ale aj smerom v rovineOh (obr. 1.8).

Obrázok 1.8
Potom projekčný modul do lietadla Oh sa bude rovnať:
Fxy = F cosα,
kde α je uhol medzi smerom sily a jeho premietanie.
Analytický spôsob špecifikácie síl
.
Pre analytickú metódu nastavenia silyje potrebné zvoliť systém súradnicových osíOhz, vo vzťahu k čomu bude určený smer sily v priestore.
Vektor znázorňujúci silu, možno zostrojiť, ak sú známy modul tejto sily a uhly α, β, γ, ktoré sila zviera so súradnicovými osami. BodkaALE použitie sily nastaviť samostatne svojimi súradnicamiX,
pri,
z. Sila môžete nastaviť podľa jej projekciífx,
fy,
fzna súradnicových osiach. Modul sily je v tomto prípade určený vzorcom:
![]()
a smerové kosínusy:
,
.
Analytická metóda sčítania síl : priemet súčtového vektora na niektorú os sa rovná algebraickému súčtu priemetov členov vektorov na tú istú os, t.j. ak:
potom , , .
Vedieť Rx, Ry, Rz, môžeme definovať modul
![]()
a smerové kosínusy:
, , .
Obrázok 1.9
Pre rovnováhu sústavy zbiehajúcich sa síl je potrebné a postačujúce, aby výslednica týchto síl bola rovná nule.1) Podmienka geometrickej rovnováhy pre konvergujúci systém síl : pre rovnováhu sústavy zbiehajúcich sa síl je potrebné a postačujúce, aby silový polygón zostrojený z týchto síl
bol uzavretý (koniec vektora posledného termínu
sila sa musí zhodovať so začiatkom vektora prvého členu sily). Potom sa hlavný vektor sústavy síl bude rovnať nule ()
2)
Podmienky analytickej rovnováhy
.
Modul hlavného vektora sústavy síl je určený vzorcom.
![]() =0. Pretože , potom sa koreňový výraz môže rovnať nule iba vtedy, ak každý člen súčasne zaniká, t.j.
=0. Pretože , potom sa koreňový výraz môže rovnať nule iba vtedy, ak každý člen súčasne zaniká, t.j.
Rx= 0, Ry= 0, R z = 0.
Preto pre rovnováhu priestorového systému zbiehajúcich sa síl je potrebné a postačujúce, aby súčty priemetov týchto síl na každú z troch súradníc osí boli rovné nule:
Pre rovnováhu plochého systému zbiehajúcich sa síl je potrebné a postačujúce, aby súčet priemetov síl na každú z dvoch súradnicových osí bol rovný nule:
Sčítanie dvoch paralelných síl v rovnakom smere.

Obrázok 1.9
Dve rovnobežné sily smerujúce rovnakým smerom sa redukujú na jednu výslednú silu rovnobežnú s nimi a smerujúcu rovnakým smerom. Veľkosť výslednice sa rovná súčtu veľkostí týchto síl a bod jej pôsobenia C rozdeľuje vzdialenosť medzi čiarami pôsobenia síl vnútorne na časti nepriamo úmerné veľkostiam týchto síl, tj.B A C
R=F 1 +F 2
Pridanie dvoch nerovnakých paralelných síl nasmerovaných v opačných smeroch.
Dve nerovnaké antiparalelné sily sú redukované na jednu výslednú silu rovnobežnú s nimi a smerujúcu k väčšej sile. Veľkosť výslednice sa rovná rozdielu medzi veľkosťami týchto síl a bod jej pôsobenia, C, rozdeľuje vzdialenosť medzi čiarami pôsobenia síl zvonka na časti nepriamo úmerné veľkostiam týchto síl. je
Dvojica síl a moment sily okolo bodu.
Moment sily
vzhľadom na bod O sa nazýva, braný s príslušným znamienkom, súčin veľkosti sily so vzdialenosťou h od bodu O k pôsobisku sily. . Tento produkt sa berie so znamienkom plus, ak je sila má tendenciu otáčať telo proti smeru hodinových ručičiek a so znamienkom -, ak je sila má tendenciu otáčať telo v smere hodinových ručičiek, tzn . Dĺžka kolmice h je tzvrameno sily
bod O. Účinok pôsobenia sily t.j. uhlové zrýchlenie telesa je tým väčšie, čím väčšia je veľkosť momentu sily.
Obrázok 1.11
Pár síl Systém sa nazýva systém pozostávajúci z dvoch rovnobežných síl rovnakej veľkosti, nasmerovaných v opačných smeroch. Vzdialenosť h medzi pôsobiskami síl sa nazývaramenné páry . Okamih dvojice síl m(F,F") je súčin hodnoty jednej zo síl, ktoré tvoria pár, a ramena páru, brané s príslušným znamienkom.Píše sa takto: m(F,F“)= ± F × h, pričom súčin sa berie so znamienkom plus, ak má dvojica síl tendenciu otáčať teleso proti smeru hodinových ručičiek a so znamienkom mínus, ak má dvojica síl tendenciu. na otáčanie tela v smere hodinových ručičiek.
Veta o súčte momentov síl dvojice.
Súčet momentov síl dvojice (F,F“) vzhľadom na ľubovoľný bod 0 zachytený v rovine pôsobenia dvojice nezávisí od výberu tohto bodu a rovná sa momentu dvojice.
Veta o ekvivalentných pároch. Dôsledky.
Veta. Dve dvojice, ktorých momenty sú si navzájom rovné, sú ekvivalentné, t.j. (F, F") ~ (P, P")
Dôsledok 1 . Dvojicu síl je možné prenášať na ľubovoľné miesto v rovine jej pôsobenia, ako aj otáčať do ľubovoľného uhla a meniť rameno a veľkosť síl dvojice pri zachovaní momentu dvojice.
Dôsledok 2. Dvojica síl nemá výslednicu a nemôže byť vyvážená jednou silou ležiacou v rovine dvojice.

Obrázok 1.12
Podmienka sčítania a rovnováhy pre sústavu dvojíc v rovine.
1. Veta o sčítaní dvojíc ležiacich v rovnakej rovine. Systém dvojíc, ľubovoľne umiestnených v rovnakej rovine, môže byť nahradený jednou dvojicou, ktorej moment sa rovná súčtu momentov týchto dvojíc.
2. Veta o rovnováhe sústavy dvojíc v rovine.
Aby bolo absolútne tuhé teleso v pokoji pri pôsobení sústavy dvojíc, ľubovoľne umiestnených v tej istej rovine, je potrebné a postačujúce, aby súčet momentov všetkých dvojíc bol rovný nule, tj.
Ťažisko
Gravitácia - výslednica príťažlivých síl k Zemi, rozložená po celom objeme telesa.
Ťažisko tela - je to taký bod, vždy spojený s týmto telesom, cez ktorý prechádza línia pôsobenia gravitačnej sily daného telesa v ktorejkoľvek polohe telesa v priestore.
Metódy hľadania ťažiska
1. Metóda symetrie:
1.1. Ak má homogénne teleso rovinu symetrie, potom ťažisko leží v tejto rovine
1.2. Ak má homogénne teleso os súmernosti, potom ťažisko leží na tejto osi. Ťažisko homogénneho rotačného telesa leží na osi otáčania.
1.3 Ak má homogénne teleso dve osi súmernosti, potom je ťažisko v bode ich priesečníka.
2. Spôsob rozdeľovania: Teleso sa rozdelí na najmenší počet častí, ktorých sú známe gravitačné sily a poloha ťažísk.
3. Metóda záporných hmotností: Pri určovaní ťažiska telesa s voľnými dutinami by sa mala použiť metóda rozdeľovania, ale hmotnosť voľných dutín by sa mala považovať za zápornú.
Súradnice ťažiska plochej postavy:

Polohy ťažísk jednoduchých geometrických útvarov možno vypočítať pomocou známych vzorcov. (Obrázok 1.13)

Poznámka: Ťažisko súmernosti postavy je na osi súmernosti.
Ťažisko tyče je v strede výšky.
1.2. Príklady riešenia praktických problémov
Príklad 1:
Závažie je zavesené na tyči a je v rovnováhe. Určte sily v tyči. (Obrázok 1.2.1)
Riešenie:
Sily, ktoré vznikajú v upevňovacích tyčiach, sú svojou veľkosťou rovnaké ako sily, ktorými tyče nesú zaťaženie. (5. axióma)
Určujeme možné smery reakcií väzieb „tuhých tyčí“.
Úsilie smeruje pozdĺž tyčí.
Obrázok 1.2.1.
Osloboďme bod A od väzieb, pričom pôsobenie väzieb nahradíme ich reakciami. (Obrázok 1.2.2)
Začnime konštrukciu so známou silou nakreslením vektoraFv určitom meradle.
Od konca vektoraFkresliť čiary rovnobežné s reakciamiR 1 aR 2 .
Obrázok 1.2.2
Pretínajúce sa čiary vytvárajú trojuholník. (Obrázok 1.2.3.). Poznaním mierky konštrukcií a meraním dĺžky strán trojuholníka je možné určiť veľkosť reakcií v tyčiach.
Na presnejšie výpočty môžete použiť geometrické vzťahy, najmä sínusovú vetu: pomer strany trojuholníka k sínusu opačného uhla je konštantná hodnota
![]()
Pre tento prípad:
Obrázok 1.2.3
![]()
komentár: Ak sa smer vektora (kopulačná reakcia) na danej schéme a v trojuholníku síl nezhoduje, potom by mala byť reakcia na schéme smerovaná opačným smerom.
Príklad 2:
Analyticky určte veľkosť a smer výslednej plochej sústavy zbiehajúcich sa síl.
Riešenie:
Obrázok 1.2.4
1. Určíme projekcie všetkých síl sústavy na Ox (obrázok 1.2.4)Algebraickým sčítaním projekcií dostaneme priemet výslednice na os Ox.

Znamienko znamená, že výslednica smeruje doľava.
2. Určíme priemety všetkých síl na os Oy:
Algebraickým sčítaním priemetov dostaneme priemet výslednice na os Oy.
Znamienko znamená, že výslednica smeruje nadol.
3. Určte modul výslednice podľa veľkostí priemetov:
4. Určte hodnotu uhla výslednice s osou Ox:
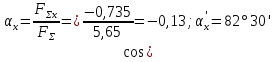
a hodnota uhla s osou y:

Príklad 3:
Vypočítajte súčet momentov síl vzhľadom na bod O (obrázok 1.2.6).
OA= AB= ATD=DE=CB=2m
Obrázok 1.2.6
Riešenie:
1. Moment sily vzhľadom na bod sa číselne rovná súčinu modulu a ramena sily.
2. Moment sily sa rovná nule, ak čiara pôsobenia sily prechádza bodom.
Príklad 4:
Určite polohu ťažiska obrázku znázorneného na obrázku 1.2.7
Riešenie:
Obrázok rozdelíme na tri:
1-obdĺžnik
ALE 1 = 10 x 20 = 200 cm 2
2-trojuholník
ALE 2 = 1/2 x 10 x 15 = 75 cm 2
3-kolový
ALE 3 =3,14*3 2 = 28,3 cm 2
Obrázok 1 CG: x 1 = 10 cm, y 1 = 5 cm
Obrázok 2 CG: x 2 =20+1/3*15=25 cm, u 2 = 1/3 x 10 = 3,3 cm
Obrázok 3 CG: x 3 = 10 cm, y 3 = 5 cm
Je definovaný podobne pre S = 4,5 cm
Kinematika: základné pojmy.
Základné kinematické parametre
Trajektória - čiara, ktorú vytyčuje hmotný bod pri pohybe v priestore. Dráha môže byť priamka a krivka, rovná a priestorová čiara.
Rovnica trajektórie pohybu v rovine: y =f ( X)
Prejdená vzdialenosť. Dráha sa meria pozdĺž cesty v smere jazdy. Označenie -S, merné jednotky - metre.
Rovnica pohybu bodu je rovnica, ktorá určuje polohu pohybujúceho sa bodu ako funkciu času.
Obrázok 2.1
Poloha bodu v každom časovom okamihu môže byť určená vzdialenosťou prejdenou pozdĺž trajektórie od nejakého pevného bodu, ktorý sa považuje za počiatok (obrázok 2.1). Tento druh pohybu sa nazývaprirodzené . Pohybovú rovnicu teda možno znázorniť ako S = f (t).

Obrázok 2.2
Polohu bodu je možné určiť aj vtedy, ak sú jeho súradnice známe ako funkcia času (obrázok 2.2). Potom v prípade pohybu po rovine musia byť dané dve rovnice:V prípade priestorového pohybu sa pridáva aj tretia súradnicaz= f 3 ( t)
Tento druh pohybu sa nazývakoordinovať .
Cestovná rýchlosť je vektorová veličina, ktorá v danom momente charakterizuje rýchlosť a smer pohybu po trajektórii.
Rýchlosť je vektor nasmerovaný v každom okamihu tangenciálne k trajektórii v smere pohybu (obrázok 2.3).
Obrázok 2.3
Ak bod pokrýva rovnaké vzdialenosti v rovnakých časových intervaloch, potom sa nazýva pohybuniforma .Priemerná rýchlosť na ceste ΔSdefinované:
kde∆S- vzdialenosť prejdená za čas Δt; Δ t- časový interval.
Ak sa bod pohybuje po nerovnakých dráhach v rovnakých časových intervaloch, potom sa pohyb nazývanerovnomerné . V tomto prípade je rýchlosť premenlivá a závisí od časuv= f( t)
Aktuálna rýchlosť je definovaná ako
bodové zrýchlenie - vektorová veličina charakterizujúca rýchlosť zmeny rýchlosti vo veľkosti a smere.
Rýchlosť bodu pri pohybe z bodu M1 do bodu Mg sa mení vo veľkosti a smere. Priemerná hodnota zrýchlenia za toto časové obdobie
Aktuálne zrýchlenie:
Zvyčajne sa pre pohodlie berú do úvahy dve vzájomne kolmé zložky zrýchlenia: normálna a tangenciálna (obrázok 2.4).
Normálne zrýchlenie a n , charakterizuje zmenu rýchlosti tým
smer a je definovaný ako
Normálne zrýchlenie je vždy smerované kolmo na rýchlosť smerom k stredu oblúka.
Obrázok 2.4
Tangenciálne zrýchlenie a t , charakterizuje zmenu rýchlosti vo veľkosti a smeruje vždy tangenciálne k trajektórii; pri zrýchlení sa jeho smer zhoduje so smerom rýchlosti a pri spomalení je nasmerovaný proti smeru vektora rýchlosti.![]()
Hodnota plného zrýchlenia je definovaná ako:
Analýza typov a kinematických parametrov pohybov
Jednotný pohyb - Ide o pohyb konštantnou rýchlosťou:
Pre priamočiary rovnomerný pohyb:
Pre krivočiary rovnomerný pohyb:
![]()
Zákon rovnomerného pohybu :
Rovnomerne premenlivý pohyb – je pohyb s konštantným tangenciálnym zrýchlením:
Pre rovnomerný priamočiary pohyb
Pre krivočiary rovnomerný pohyb:
![]()
Zákon rovnomerného pohybu:
![]()
Kinematické grafy
Kinematické grafy - Ide o grafy zmien dráhy, rýchlosti a zrýchlenia v závislosti od času.
Rovnomerný pohyb (obrázok 2.5)

Obrázok 2.5
Rovnomerne premenlivý pohyb (obrázok 2.6)

Obrázok 2.6
Najjednoduchšie pohyby tuhého telesa
Pohyb vpred nazývaný pohyb tuhého telesa, pri ktorom akákoľvek priamka na tele počas pohybu zostáva rovnobežná s jeho počiatočnou polohou (obrázok 2.7)

Obrázok 2.7
Pri translačnom pohybe sa všetky body tela pohybujú rovnakým spôsobom: rýchlosti a zrýchlenia sú v každom okamihu rovnaké.
orotačný pohyb
všetky body tela opisujú kruhy okolo spoločnej pevnej osi.
Pevná os, okolo ktorej sa otáčajú všetky body telesa, sa nazývaos otáčania.
Iba na opísanie rotačného pohybu telesa okolo pevnej osirohové možnosti. (Obrázok 2.8)
φ je uhol natočenia tela;
ω – uhlová rýchlosť, určuje zmenu uhla natočenia za jednotku času;
Zmena uhlovej rýchlosti s časom je určená uhlovým zrýchlením:
2.2. Príklady riešenia praktických problémov
Príklad 1: Je daná pohybová rovnica bodu. Určte rýchlosť bodu na konci tretej sekundy pohybu a priemernú rýchlosť počas prvých troch sekúnd.
![]()
Riešenie:
1. Rovnica rýchlosti
2. Rýchlosť na konci tretej sekundy (t=3 c)
3. Priemerná rýchlosť
Príklad 2: Podľa daného pohybového zákona určte druh pohybu, počiatočnú rýchlosť a tangenciálne zrýchlenie bodu, čas do zastavenia.
![]()
Riešenie:
1. Typ pohybu: rovnako variabilný (![]() )
)
2. Pri porovnávaní rovníc je zrejmé, že
- počiatočná dráha prejdená pred začiatkom odpočítavania 10 m;
- počiatočná rýchlosť 20 m/s
- konštantné tangenciálne zrýchlenie ![]()
- zrýchlenie je záporné, preto je pohyb pomalý, zrýchlenie smeruje v opačnom smere ako je rýchlosť pohybu.
3. Môžete určiť čas, v ktorom sa rýchlosť bodu bude rovnať nule.
3. Dynamika: základné pojmy a axiómy
Dynamika - oddiel teoretickej mechaniky, v ktorom sa vytvára súvislosť medzi pohybom telies a silami, ktoré na ne pôsobia.
V dynamike sa riešia dva typy problémov:
určiť parametre pohybu podľa daných síl;
určiť sily pôsobiace na teleso, podľa daných kinematických parametrov pohybu.
Podhmotný bod
implikujú určité teleso, ktoré má určitú hmotnosť (t. j. obsahuje určité množstvo hmoty), ale nemá lineárne rozmery (nekonečne malý objem priestoru).
izolovaný
uvažuje sa o hmotnom bode, ktorý nie je ovplyvnený inými hmotnými bodmi. V skutočnom svete neexistujú izolované hmotné body, ako aj izolované telá, tento koncept je podmienený.
Pri translačnom pohybe sa všetky body telesa pohybujú rovnakým spôsobom, takže teleso možno brať ako hmotný bod.
Ak sú rozmery telesa v porovnaní s trajektóriou malé, možno ho považovať aj za hmotný bod, pričom bod sa zhoduje s ťažiskom telesa.
Pri rotačnom pohybe telesa sa body nemusia pohybovať rovnakým spôsobom, v tomto prípade možno niektoré ustanovenia dynamiky aplikovať len na jednotlivé body a hmotný objekt možno považovať za súbor hmotných bodov.
Preto sa dynamika delí na dynamiku bodu a dynamiku hmotného systému.
Axiómy dynamiky
Prvá axióma ( princíp zotrvačnosti): v každý izolovaný hmotný bod je v stave pokoja alebo rovnomerného a priamočiareho pohybu, kým ho aplikované sily nevyvedú z tohto stavu.
Tento stav sa nazýva štátzotrvačnosť. Odstráňte bod z tohto stavu, t.j. daj tomu nejaké zrýchlenie, možno vonkajšiu silu.
Každé telo (bod) mázotrvačnosť. Mierou zotrvačnosti je hmotnosť telesa.
omša volalmnožstvo hmoty v tele v klasickej mechanike sa považuje za konštantnú hodnotu. Jednotkou hmotnosti je kilogram (kg).
Druhá axióma (Druhý Newtonov zákon je základným zákonom dynamiky)
F=ma
kdet - hmotnosť bodu, kg;a - bodové zrýchlenie, m/s 2 .
Zrýchlenie udelené hmotnému bodu silou je úmerné veľkosti sily a zhoduje sa so smerom sily.
Gravitácia pôsobí na všetky telesá na Zemi, udeľuje telu zrýchlenie voľného pádu smerujúceho do stredu Zeme:
G = mg
kdeg- 9,81 m/s², zrýchlenie voľného pádu.
Tretia axióma (tretí Newtonov zákon): sSily interakcie dvoch telies sú rovnakej veľkosti a smerujú pozdĺž tej istej priamky v rôznych smeroch.
Pri interakcii sú zrýchlenia nepriamo úmerné hmotnosti.
Štvrtá axióma (zákon nezávislosti pôsobenia síl): doKaždá sila sústavy síl pôsobí tak, ako by pôsobila samostatne.
Zrýchlenie udelené bodu systémom síl sa rovná geometrickému súčtu zrýchlení udelených bodu každou silou samostatne (obrázok 3.1):

Obrázok 3.1
Pojem trenie. Druhy trenia.
Trenie-
odpor vznikajúci pri pohybe jedného drsného telesa na povrchu druhého. Klzné trenie má za následok klzné trenie a valivé trenie má za následok kývavé trenie.
Klzné trenie
Obrázok 3.2.
Dôvodom je mechanický záber výstupkov. Sila odporu voči pohybu počas kĺzania sa nazýva sila klzného trenia (obrázok 3.2).Zákony klzného trenia:
1. Sila klzného trenia je priamo úmerná sile normálneho tlaku: 
kdeR- sila normálneho tlaku, smerujúca kolmo na nosnú plochu;f- koeficient klzného trenia.
Obrázok 3.3.
V prípade telesa pohybujúceho sa pozdĺž naklonenej roviny (obrázok 3.3)valivé trenie
Valivý odpor súvisí so vzájomnou deformáciou zeme a kolesa a je oveľa menší ako klzné trenie.
Pre rovnomerné odvaľovanie kolesa je potrebné vyvinúť siluF dv (Obrázok 3.4)
Podmienkou odvaľovania kolesa je, že pohybový moment nesmie byť menší ako moment odporu:
Obrázok 3.4.
Príklad 1: Príklad 2: Do dvoch hmotných bodovm 1 = 2 kg am 2 = 5 kg aplikujú sa rovnaké sily. Porovnajte hodnoty rýchlejšie.Riešenie:
Podľa tretej axiómy je dynamika zrýchlenia nepriamo úmerná hmotnosti: ![]()
Príklad 3:
Určte prácu gravitácie pri premiestňovaní bremena z bodu A do bodu C po naklonenej rovine (obrázok 3. 7). Gravitačná sila telesa je 1500N. AB = 6 m, BC = 4 m. Príklad 3:
Určte prácu reznej sily za 3 minúty. Rýchlosť otáčania obrobku je 120 ot./min., priemer obrobku je 40 mm, rezná sila je 1 kN. (Obrázok 3.8)
Riešenie:
1. Práca s rotačným pohybom:
2. Uhlová rýchlosť 120 ot./min
Obrázok 3.8.
3. Počet otáčok za daný čas jez\u003d 120 * 3 \u003d 360 ot.Uhol natočenia počas tejto doby φ=2πz\u003d 2 * 3,14 * 360 \u003d 2261 rad
4. Pracujte na 3 otáčky:W\u003d 1 * 0,02 * 2261 \u003d 45,2 kJ
Bibliografia
Olofinskaja, V.P. "Technická mechanika", Moskva "Fórum" 2011
Erdedi A.A. Erdedi N.A. Teoretická mechanika. Pevnosť materiálov.- R-n-D; Phoenix, 2010