Mechanikos paskaitų konspektai. Techninė mechanika

1 skaidrė

Teorinės mechanikos paskaitų kursas Dinamika (I dalis) Bondarenko A.N. Maskva – 2007 Elektroninis mokymo kursas buvo parašytas remiantis autoriaus skaitomomis paskaitomis studentams, kurie studijavo SZD, PGS ir SDM specialybes NIIZhT ir MIIT (1974-2006). Mokomoji medžiaga atitinka trijų semestrų apimties kalendorinius planus. Norėdami visiškai pritaikyti animacijos efektus pristatymo metu, turite naudoti Power Point peržiūros programą, ne žemesnę nei įdiegta Windows XP Professional operacinės sistemos Microsoft Office. Pastabas ir pasiūlymus galima siųsti el. [apsaugotas el. paštas]... Maskvos valstybinio geležinkelių inžinerijos universiteto (MIIT) Teorinės mechanikos katedros Transporto technologijų mokslinis ir techninis centras

2 skaidrė

Turinys Paskaita 1. Įvadas į dinamiką. Materialaus taško dinamikos dėsniai ir aksiomos. Pagrindinė dinamikos lygtis. Diferencialinės ir natūraliosios judėjimo lygtys. Du pagrindiniai dinamikos uždaviniai. Tiesioginės dinamikos problemos sprendimo pavyzdžiai 2 paskaita. Atvirkštinės dinamikos problemos sprendimas. Bendrieji atvirkštinės dinamikos uždavinio sprendimo nurodymai. Atvirkštinės dinamikos problemos sprendimo pavyzdžiai. Kūno, mesto kampu į horizontą, judėjimas, neatsižvelgiant į oro pasipriešinimą. 3 paskaita. Materialaus taško tiesiniai virpesiai. Vibracijos atsiradimo sąlyga. Vibracijų klasifikacija. Laisvos vibracijos neatsižvelgiant į pasipriešinimo jėgas. Slopinti svyravimai. Svyravimų mažinimas. 4 paskaita. Priverstiniai materialaus taško svyravimai. Rezonansas. Atsparumo judėjimui poveikis priverstinės vibracijos metu. 5 paskaita. Materialaus taško santykinis judėjimas. Inercijos jėgos. Ypatingi judėjimo atvejai įvairių tipų nešiojamiesiems judesiams. Žemės sukimosi įtaka kūnų pusiausvyrai ir judėjimui. Paskaita 6. Mechaninės sistemos dinamika. Mechaninė sistema. Išorinės ir vidinės jėgos. Sistemos masės centras. Masės centro judėjimo teorema. Apsaugos įstatymai. Uždavinio sprendimo pavyzdys naudojant masės centro judėjimo teoremą. 7 paskaita. Jėgos impulsas. Judėjimo kiekis. Judesio kiekio kitimo teorema. Apsaugos įstatymai. Eilerio teorema. Impulso keitimo teoremos panaudojimo problemos sprendimo pavyzdys. Impulso momentas. Teorema apie kampinio momento kitimą.. 8 paskaita. Konservavimo dėsniai. Inercijos momentų teorijos elementai. Kinetinis standaus kūno momentas. Standaus kūno sukimosi diferencialinė lygtis. Sistemos kampinio momento kitimo teoremos panaudojimo uždavinio sprendimo pavyzdys. Elementari giroskopo teorija. Rekomenduojama literatūra 1. Yablonskiy A.A. Teorinės mechanikos kursas. 2 dalis. M .: Aukštoji mokykla. 1977 368 s. 2. Meshchersky I.V. Teorinės mechanikos uždavinių rinkinys. M .: Mokslas. 1986 416 s. 3. Kursinių darbų užduočių rinkinys / Red. A.A. Jablonskis. M.: Aukštoji mokykla. 1985 366 p. 4. Bondarenko A. N. „Teorinė mechanika pavyzdžiuose ir uždaviniuose. Dinamika “(elektroninis vadovas www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004 m.

3 skaidrė

1 paskaita Dinamika yra teorinės mechanikos šaka, tirianti mechaninį judėjimą bendriausiu požiūriu. Judėjimas laikomas ryšium su jėgomis, veikiančiomis objektą. Skyrius susideda iš trijų sekcijų: Materialaus taško dinamika Mechaninės sistemos dinamika Analitinė mechanika ■ Taško dinamika – tiria materialaus taško judėjimą atsižvelgiant į jėgas, kurios sukelia šį judėjimą. Pagrindinis objektas yra materialus taškas – materialus kūnas, turintis masę, kurio matmenų galima nepaisyti. Pagrindinės prielaidos: - yra absoliuti erdvė (ji turi grynai geometrines savybes, kurios nepriklauso nuo materijos ir jos judėjimo. - yra absoliutus laikas (nepriklauso nuo materijos ir jos judėjimo). Iš to išplaukia: - yra absoliučiai nejudanti atskaitos sistema. - laikas nepriklauso nuo atskaitos sistemos judėjimo. - judančių taškų masės nepriklauso nuo atskaitos sistemos judėjimo. Šios prielaidos naudojamos klasikinėje mechanikoje, sukurtoje Galileo ir Niutonas.Jis vis dar turi gana platų pritaikymo sritį, kadangi taikomuosiuose moksluose nagrinėjamos mechaninės sistemos neturi tokių didelių masių ir judėjimo greičių, kuriems reikėtų atsižvelgti į jų įtaką erdvės, laiko geometrijai. , judėjimas, kaip tai daroma reliatyvistinėje mechanikoje (reliatyvumo teorijoje). Jų dinaminė sąveika Veiksmai veikiami įvairių jėgų. ■ Inercijos dėsnis (Galileo-Niutono dėsnis) – izoliuotas materialus taškas, kūnas išlaiko ramybės būseną arba tolygų tiesinį judėjimą tol, kol veikiančios jėgos priverčia jį pakeisti šią būseną. Tai reiškia ramybės būsenos ir judėjimo lygiavertiškumą pagal inerciją (Galilėjaus reliatyvumo dėsnis). Atskaitos sistema, kurios atžvilgiu įvykdomas inercijos dėsnis, vadinama inercija. Materialaus taško savybė stengtis išlaikyti nepakitusią jo judėjimo greitį (kinematinę būseną) vadinama inercija. ■ Jėgos ir pagreičio proporcingumo dėsnis (pagrindinė dinamikos lygtis – Niutono II dėsnis) – pagreitis, kurį jėga suteikia materialiam taškui, yra tiesiogiai proporcingas jėgai ir atvirkščiai proporcingas šio taško masei: arba Čia m yra taško masė (inercijos matas), matuojama kg, skaitinis lygus svoris, padalintas iš sunkio pagreičio: F yra veikianti jėga, išmatuota N (1 N suteikia 1 m/s2 pagreitį taškui, kurio masė 1 kg, 1 N = 1/9. 81 kg). ■ Mechaninės sistemos dinamika – tiria materialių taškų ir kietųjų kūnų aibės judėjimą, kurį vienija bendrieji sąveikos dėsniai, atsižvelgiant į šį judėjimą sukeliančias jėgas. ■ Analitinė mechanika – tiria nelaisvųjų mechaninių sistemų judėjimą taikant bendruosius analizės metodus. 1

4 skaidrė

1 paskaita (tęsinys - 1.2) Materialaus taško judėjimo diferencialinės lygtys: - taško judėjimo diferencialinė lygtis vektorine forma. - taško judėjimo diferencialinės lygtys koordinačių pavidalu. Šis rezultatas gali būti gaunamas formaliai projekuojant vektorinę diferencialinę lygtį (1). Po sugrupavimo vektorinis ryšys suskaidomas į tris skaliarines lygtis: Koordinačių forma: Mes naudojame spindulio vektoriaus ryšį su koordinatėmis ir jėgos vektoriaus ryšį su projekcijomis: arba: Taško pagreitį judesio vektoriaus nustatyme pakeiskite į pagrindinė dinamikos lygtis: Natūralios materialaus taško judėjimo lygtys gaunamos projektuojant vektorinę diferencialinę judėjimo lygtį ant natūralių (judančių) koordinačių ašių: arba: - natūraliosios taško judėjimo lygtys. ■ Pagrindinė dinamikos lygtis: - atitinka vektorinį taško judėjimo patikslinimo metodą. ■ Jėgų veikimo nepriklausomybės dėsnis – Materialaus taško pagreitis, veikiant kelioms jėgoms, yra lygus taško pagreičių geometrinei sumai, veikiant kiekvienai jėgai atskirai: arba galioja dėsnis. bet kuriai kinematinei kūnų būsenai. Sąveikos jėgos, taikomos skirtingiems taškams (kūnams), nėra subalansuotos. ■ Veiksmo ir reakcijos lygybės dėsnis (III Niutono dėsnis) – kiekvienas veiksmas atitinka vienodo dydžio ir priešingos krypties reakciją: 2

5 skaidrė

Dvi pagrindinės dinamikos problemos: 1. Tiesioginė problema: Pateikiamas judėjimas (judesio lygtys, trajektorija). Būtina nustatyti jėgas, kurioms veikiant vyksta tam tikras judėjimas. 2. Atvirkštinė problema: jėgos, kurioms veikiant vyksta judėjimas. Būtina rasti judėjimo parametrus (judesio lygtis, judėjimo trajektoriją). Abi problemos sprendžiamos naudojant pagrindinę dinamikos lygtį ir jos projekciją į koordinačių ašis. Jei atsižvelgiama į nelaisvo taško judėjimą, tada, kaip ir statikoje, naudojamas laisvės nuo ryšių principas. Dėl reakcijos ryšiai įtraukiami į jėgų, veikiančių materialųjį tašką, sudėtį. Pirmosios problemos sprendimas siejamas su diferenciacijos operacijomis. Norint išspręsti atvirkštinę problemą, reikia integruoti atitinkamas diferencialines lygtis, o tai yra daug sunkiau nei diferencijuoti. Atvirkštinė problema yra sudėtingesnė nei tiesioginė problema. Panagrinėkime tiesioginės dinamikos problemos sprendimą pavyzdžiais: 1 pavyzdys. Lifto kabina, kurios svoris G, pakeliamas lynu, kurio pagreitis a. Nustatykite kabelio įtempimą. 1. Parenkame objektą (lifto kabina juda laipsniškai ir jį galima laikyti materialiu tašku). 2. Išmeskite jungtį (kabelį) ir pakeiskite reakcija R. 3. Sudarykite pagrindinę dinamikos lygtį: Nustatykite kabelio reakciją: Nustatykite troso įtempimą: Tolygiai judant kabinai ay = 0 ir įtempimui troso lygus svoriui: T = G. Nutrūkus trosui T = 0 ir kabinos pagreitis lygus sunkio jėgos pagreičiui: ay = -g. 3 4. Suprojektuokime pagrindinę dinamikos lygtį y ašyje: y Pavyzdys 2. Masės taškas m juda horizontaliu paviršiumi (Oxy plokštuma) pagal lygtis: x = a coskt, y = b coskt. Nustatykite tašką veikiančią jėgą. 1. Pasirinkite objektą (medžiaginį tašką). 2. Išmeskite ryšį (plokštumą) ir pakeiskite reakcija N. 3. Į jėgų sistemą įtraukite nežinomą jėgą F. 4. Sudarykite pagrindinę dinamikos lygtį: 5. Suprojektuokite pagrindinę dinamikos lygtį x, y ašyse. : Nustatykite jėgos projekcijas: Jėgos modulis: Krypties kosinusai : Taigi jėgos dydis yra proporcingas taško atstumui nuo koordinačių centro ir yra nukreiptas į centrą išilgai linijos, jungiančios tašką su centru. Taško trajektorija yra elipsė, kurios centras yra pradžioje: O r 1 paskaita (tęsinys - 1.3)

6 skaidrė

1 paskaita (tęsinys 1.4) 3 pavyzdys: G svorio krovinys pakabinamas ant l ilgio troso ir juda apskritimu horizontalioje plokštumoje tam tikru greičiu. Kabelio nuokrypio kampas nuo vertikalės yra lygus. Nustatykite lyno įtempimą ir apkrovos greitį. 1. Pasirinkite objektą (krovinį). 2. Išmetame jungtį (kabelį) ir pakeičiame reakcija R. 3. Sudarome pagrindinę dinamikos lygtį: Iš trečiosios lygties nustatome kabelio reakciją: Nustatome kabelio įtempimą: Pakeiskite kabelio reakciją, normalų pagreitį į antrą lygtį ir nustatyti apkrovos greitį: 4. Suprojektuokite pagrindinės lygties dinamiką ant ašies, n, b: 4 pavyzdys: Automobilis, kurio svoris G juda išgaubtu tiltu (kreivio spindulys yra R) greičiu V. Nustatykite automobilio slėgį ant tilto. 1. Išsirenkame objektą (automobilį, nepaisome matmenų ir laikome tašku). 2. Išmetame jungtį (šiurkštų paviršių) ir pakeičiame reakcijomis N ir trinties jėga Ffr. 3. Sudarome pagrindinę dinamikos lygtį: 4. Projektuojame pagrindinę dinamikos lygtį ašyje n: Iš čia nustatome normaliąją reakciją: Nustatome automobilio slėgį ant tilto: Iš čia galime nustatyti greitį atitinkantis nulinį tilto slėgį (Q = 0): 4

7 skaidrė

2 paskaita Pakeitę rastąsias konstantų vertes, gauname: Taigi, veikiant tai pačiai jėgų sistemai, materialus taškas gali atlikti visą judesių klasę, kurią nustato pradinės sąlygos. Pradinės koordinatės atsižvelgia į taško pradžią. Pradinis greitis, pateiktas projekcijomis, atsižvelgia į jėgų, veikiančių tašką prieš atvykstant į šią atkarpą, poveikį jo judėjimui nagrinėjamoje trajektorijos atkarpoje, t.y. pradinė kinematinė būsena. Atvirkštinės dinamikos problemos sprendimas – Bendru atveju tašką veikiančio jėgos taško judėjimas yra kintamieji, kurie priklauso nuo laiko, koordinačių ir greičio. Taško judėjimas apibūdinamas trijų antros eilės diferencialinių lygčių sistema: Integravus kiekvieną iš jų, bus šešios konstantos C1, C2,…., C6: Konstantų C1, C2,... ., C6 randami iš šešių pradinių sąlygų, kai t = 0: 1 sprendimo pavyzdys atvirkštinė problema: Laisvas medžiagos taškas, kurio masė m, juda veikiant jėgai F, kurios dydis ir dydis yra pastovūs. ... Pradiniu momentu taško greitis buvo v0 ir sutapo kryptimi su jėga. Nustatykite taško judėjimo lygtį. 1. Sudarykite pagrindinę dinamikos lygtį: 3. Sumažinkite išvestinės eilę: 2. Pasirinkite Dekarto atskaitos sistemą, nukreipiančią x ašį išilgai jėgos krypties ir projektuokite pagrindinę dinamikos lygtį šioje ašyje: arba xyz 4. Atskirkite kintamuosius: 5. Apskaičiuokite abiejų lygties pusių integralus: 6. Greičio projekciją pavaizduojame kaip koordinatės išvestinę laiko atžvilgiu: 8. Apskaičiuojame abiejų lygties pusių integralus. lygtis: 7. Atskirkite kintamuosius: 9. Norėdami nustatyti konstantų C1 ir C2 reikšmes, naudojame pradines sąlygas t = 0, vx = v0, x = x0: Rezultate gauname lygtį tolygus judėjimas (išilgai x ašies): 5

8 skaidrė

Bendrosios tiesioginės ir atvirkštinės problemos sprendimo instrukcijos. Sprendimo eiga: 1. Judėjimo diferencialinės lygties sudarymas: 1.1. Pasirinkite koordinačių sistemą – stačiakampę (fiksuotą) su nežinoma judėjimo trajektorija, natūralią (judinamą) su žinoma trajektorija, pavyzdžiui, apskritimą arba tiesią. Pastaruoju atveju gali būti naudojama viena tiesi koordinatė. Sulygiuokite pradinę vietą su pradine taško padėtimi (kai t = 0) arba su taško pusiausvyros padėtimi, jei ji egzistuoja, pavyzdžiui, kai taškas vibruoja. 6 1.2. Nubrėžkite tašką padėtyje, atitinkančioje savavališką laiko momentą (jei t> 0), kad koordinatės būtų teigiamos (s> 0, x> 0). Šiuo atveju taip pat darome prielaidą, kad greičio projekcija šioje padėtyje taip pat yra teigiama. Virpesių atveju greičio projekcija keičia ženklą, pavyzdžiui, grįžus į pusiausvyros padėtį. Čia reikėtų daryti prielaidą, kad nagrinėjamu laiko momentu taškas nutolsta nuo pusiausvyros padėties. Ši rekomendacija yra svarbi ateityje dirbant su nuo greičio priklausančiomis pasipriešinimo jėgomis. 1.3. Atlaisvinkite materialųjį tašką nuo ryšių, pakeiskite jų veikimą reakcijomis, pridėkite aktyvias jėgas. 1.4. Užrašykite pagrindinį dinamikos dėsnį vektorine forma, projektuokite ant pasirinktų ašių, išreikškite duotąsias arba reaktyviąsias jėgas laiko kintamaisiais, koordinatėmis ar greičiais, jei jie nuo jų priklauso. 2. Diferencialinių lygčių sprendimas: 2.1. Sumažinkite išvestinę, jei lygtis nesumažinama iki kanoninės (standartinės) formos. pavyzdžiui: arba 2.2. Padalinkite kintamuosius, pavyzdžiui: arba 2.4. Apskaičiuokite neapibrėžtuosius integralus kairėje ir dešinėje lygties pusėse, pavyzdžiui: 2.3. Jei lygtyje yra trys kintamieji, tada pakeiskite kintamuosius, pavyzdžiui: ir tada padalinkite kintamuosius. komentuoti. Užuot skaičiuoję neapibrėžtus integralus, galite apskaičiuoti apibrėžtuosius integralus su kintama viršutine riba. Apatinės ribos reiškia pradines kintamųjų reikšmes (pradines sąlygas). Tada nereikia atskirai nustatyti konstantos, kuri automatiškai įtraukiama į sprendimą, pvz.: Naudojant pradines sąlygas, pvz., t = 0 , vx = vx0, nustatykite integravimo konstantą: 2.5. Išreikškite greitį koordinačių išvestine laike, pavyzdžiui, ir pakartokite 2.2–2.4 punktus. Jei lygtis sumažinama iki kanoninės formos, kuri turi standartinį tirpalą, tada naudojamas šis paruoštas sprendimas. Integravimo konstantos vis dar randamos iš pradinių sąlygų. Žr., pavyzdžiui, dvejones (4 paskaita, p. aštuoni). 2 paskaita (tęsinys 2.2)

9 skaidrė

2 paskaita (tęsinys 2.3) 2 atvirkštinio uždavinio sprendimo pavyzdys: Jėga priklauso nuo laiko. Svorio P krovinys pradeda judėti lygiu horizontaliu paviršiumi, veikiant jėgai F, kurios reikšmė proporcinga laikui (F = kt). Nustatykite krovinio nuvažiuotą atstumą laiku t. 3. Sudarykite pagrindinę dinamikos lygtį: 5. Sumažinkite išvestinės eilę: 4. Suprojektuokite pagrindinę dinamikos lygtį x ašyje: arba 7 6. Atskirkite kintamuosius: 7. Apskaičiuokite abiejų pusių integralus. lygtis: 9. Pavaizduokime greičio projekciją kaip koordinatės laiko išvestinę: 10. Apskaičiuokite abiejų lygties pusių integralus: 9. Atskirkite kintamuosius: 8. Nustatykite konstantos C1 reikšmę iš pradinės. sąlyga t = 0, vx = v0 = 0: Rezultate gauname judėjimo lygtį (išilgai x ašies), kuri suteikia nuvažiuoto atstumo reikšmę per laiką t: 1. Pasirenkame atskaitos sistemą ( Dekarto koordinates), kad kūnas turėtų teigiamą koordinatę: 2. Judėjimo objektą imame kaip materialųjį tašką (kūnas juda transliaciniu būdu), atleidžiame nuo ryšio (atskaitos plokštumos) ir pakeičiame reakcija (normali reakcija lygus paviršius) : 11. Nustatykite konstantos C2 reikšmę iš pradinės sąlygos t = 0, x = x0 = 0: Atvirkštinio uždavinio sprendimo 3 pavyzdys: Jėga priklauso nuo koordinatės. Materialus taškas, kurio masė yra m, yra išmestas aukštyn nuo Žemės paviršiaus v0 greičiu. Žemės gravitacija yra atvirkščiai proporcinga atstumo nuo taško iki gravitacijos centro (Žemės centro) kvadratui. Nustatykite greičio priklausomybę nuo atstumo y iki Žemės centro. 1. Pasirenkame atskaitos sistemą (Dekarto koordinates), kad kūnas turėtų teigiamą koordinatę: 2. Sudarome pagrindinę dinamikos lygtį: 3. Projektuojame pagrindinę dinamikos lygtį y ašyje: arba Koeficientas proporcingumą galima rasti naudojant Žemės paviršiaus taško svorį: R Taigi lygtis atrodo taip: arba 4. Sumažinkite išvestinės eilę: 5. Pakeiskite kintamąjį: 6. Atskirkite kintamuosius: 7. Apskaičiuokite abiejų lygties pusių integralus: 8. Pakeiskite ribas: Rezultate gauname greičio išraišką kaip y koordinatės funkciją: Didžiausią skrydžio aukštį greitį galima rasti prilyginus greitį nulis: Didžiausias skrydžio aukštis, kai vardiklis išnyksta: Taigi, nustatant Žemės spindulį ir gravitacinį pagreitį, gaunamas II kosminis greitis:

10 skaidrės

2 paskaita (tęsinys 2.4) 2 atvirkštinio uždavinio sprendimo pavyzdys: Jėga priklauso nuo greičio. m masės laivo greitis buvo v0. Vandens pasipriešinimas laivo judėjimui yra proporcingas greičiui. Nustatykite laiką, per kurį valties greitis sumažės per pusę išjungus variklį, taip pat atstumą, kurį valtis nuvažiuos iki visiško sustojimo. 8 1. Pasirenkame atskaitos sistemą (Dekarto koordinates), kad kūnas turėtų teigiamą koordinatę: 2. Judėjimo objektą imame materialiu tašku (laivas juda į priekį), atlaisviname jį nuo ryšių (vandens) ir pakeiskite ją reakcija (plūduriuojančia jėga – Archimedo jėga), taip pat pasipriešinimo judėjimui jėga. 3. Pridėkite aktyviąją jėgą (gravitaciją). 4. Sudarykite pagrindinę dinamikos lygtį: 5. Suprojektuokite pagrindinę dinamikos lygtį x ašyje: arba 6. Sumažinkite išvestinės eilę: 7. Atskirkite kintamuosius: 8. Apskaičiuokite abiejų pusių integralus. lygtis: 9. Pakeiskite ribas: Gaunama išraiška, kuri susieja greitį ir laiką t, iš kurios galima nustatyti judėjimo laiką: Judėjimo laikas, per kurį greitis sumažės per pusę: Įdomu pastebėti, kad greičiui artėjant prie nulio, judėjimo laikas linkęs į begalybę, t galutinis greitis negali būti lygus nuliui. Ar tai ne „amžinas judėjimas“? Tačiau nuvažiuotas atstumas iki stotelės yra galutinė vertė. Norėdami nustatyti nuvažiuotą atstumą, kreipiamės į išraišką, gautą sumažinus išvestinės eilę, ir atliekame kintamojo pakeitimą: Integravę ir pakeitę ribas gauname: Nuvažiuotas atstumas iki stotelės: ■ Judėjimas taškas, išmestas kampu į horizontą vienodame gravitacijos lauke, neatsižvelgiant į oro pasipriešinimą Iš judėjimo lygčių pašalinus laiką, gauname trajektorijos lygtį: Skrydžio laikas nustatomas prilyginus y koordinatę nuliui: Skrydžio nuotolis nustatomas pakeičiant skrydžio laiką:

11 skaidrė

3 paskaita Tiesieji materialaus taško svyravimai – Materialaus taško svyruojantis judėjimas vyksta esant sąlygai: yra atkuriamoji jėga, kuri linkusi grąžinti tašką į pusiausvyros padėtį bet kokiam nukrypimui nuo šios padėties. 9 Yra atkuriamoji jėga, pusiausvyros padėtis yra stabili Atkuriamosios jėgos nėra, pusiausvyros padėtis nestabili Atkuriamosios jėgos nėra, pusiausvyros padėtis yra abejinga. Jis visada nukreiptas į pusiausvyros padėtį, vertė yra tiesiogiai proporcinga spyruoklės linijiniam pailgėjimui (sutrumpėjimui), lygi kūno nuokrypiui nuo pusiausvyros padėties: c spyruoklės standumo koeficientas, skaičiais lygus jėgai. pagal kurią spyruoklė keičia savo ilgį vienu, matuojant N / m sistemoje SI. x y O Medžiagos taško virpesių rūšys: 1. Laisvosios vibracijos (neatsižvelgiant į terpės varžą). 2. Laisvos vibracijos, atsižvelgiant į terpės atsparumą (slopintos vibracijos). 3. Priverstinės vibracijos. 4. Priverstinės vibracijos atsižvelgiant į terpės varžą. ■ Laisvos vibracijos – atsiranda veikiant tik atkuriančiajai jėgai. Užrašykime pagrindinį dinamikos dėsnį: Pasirinkite koordinačių sistemą, kurios centras yra pusiausvyros padėtyje (taške O), ir projektuokite lygtį į x ašį: Sumažinkite gautą lygtį iki standartinės (kanoninės) formos: Ši lygtis yra antrojo laipsnio vienalytė tiesinė diferencialinė lygtis, kurios sprendimo formą lemia charakteristikos šaknys lygtis gauta naudojant universalųjį pakeitimą: Charakteristikos lygties šaknys yra įsivaizduojamos ir lygios: Bendrasis diferencialinės lygties sprendimas turi tokią formą: Taško greitis: Pradinės sąlygos: Apibrėžkite konstantas: Taigi, laisvųjų virpesių lygtis turi tokią formą: Lygtį galima pavaizduoti vienanarė išraiška: - pradinė fazė. Naujos konstantos a ir - yra susietos su konstantomis C1 ir C2 ryšiais: Nustatykime a ir: Laisvųjų svyravimų atsiradimo priežastis yra pradinis poslinkis x0 ir/arba pradinis greitis v0.

12 skaidrė

10 3 paskaita (tęsinys 3.2) Slopinti materialaus taško svyravimai – Materialaus taško svyruojantis judėjimas vyksta esant atkuriančiajai jėgai ir pasipriešinimo judėjimui jėgai. Pasipriešinimo judesiui jėgos priklausomybę nuo poslinkio ar greičio lemia fizinės terpės arba ryšio, kuri neleidžia judėti, prigimtis. Paprasčiausia priklausomybė yra tiesinė priklausomybė nuo greičio (klampios varžos): - klampumo koeficientas xy O Pagrindinė dinamikos lygtis: Dinamikos lygties projekcija ašyje: Paveskime lygtį į standartinę formą: kur Charakteristikos lygtis turi šaknys: Bendras šios diferencialinės lygties sprendimas turi skirtingą formą, priklausomai nuo šaknų reikšmių: 1.n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - didelio klampumo atvejis: - tikros šaknys, skirtingos. arba - šios funkcijos yra aperiodinės: 3. n = k: - tikrosios daugybinės šaknys. šios funkcijos taip pat yra periodinės:

13 skaidrė

3 paskaita (tęsinys 3.3) Laisvųjų virpesių sprendinių klasifikacija. Spyruoklių prijungimo būdai. Lygiavertis standumas. y y 11 Skirt. lygtis Charakteris. lygtis Šaknų simbolis. lygtys Diferencialinės lygties sprendimas Grafas nk n = k

14 skaidrė

4 paskaita Priverstiniai materialaus taško virpesiai – kartu su atkuriančia jėga veikia periodiškai besikeičianti jėga, vadinama trikdančia jėga. Trikdanti jėga gali būti kitokio pobūdžio. Pavyzdžiui, konkrečiu atveju inercinis besisukančio rotoriaus nesubalansuotos masės m1 poveikis sukelia harmoningai besikeičiančias jėgos projekcijas: Pagrindinė dinamikos lygtis: Dinamikos lygties projekcija į ašį: Lygtį perkelkime į standartinė forma: 12 Šios nevienalytės diferencialinės lygties sprendimas susideda iš dviejų dalių x = x1 + x2: x1 yra bendras atitinkamos vienalytės lygties sprendinys, o x2 yra konkretus nehomogeninės lygties sprendinys: Mes pasirenkame konkretų sprendimą formoje dešiniosios pusės: Gauta lygybė turi būti tenkinama bet kuriai t. Tada: arba Taigi, tuo pačiu metu veikiant atkuriančioms ir trikdančioms jėgoms, materialus taškas atlieka sudėtingą svyruojantį judesį, kuris yra laisvųjų (x1) ir priverstinių (x2) virpesių pridėjimo (superpozicijos) rezultatas. Jei p< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (priverstiniai aukšto dažnio virpesiai), tada svyravimų fazė yra priešinga trikdančios jėgos fazei:

15 skaidrė

4 paskaita (tęsinys 4.2) 13 Dinaminis koeficientas – tai priverstinių virpesių amplitudės ir taško statinio įlinkio, veikiant pastoviai jėgai, santykis H = const: Priverstinių virpesių amplitudė: Statinį įlinkį galima rasti iš pusiausvyros lygtis: Čia: Taigi: Taigi, p< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (didelis priverstinių virpesių dažnis) dinaminis faktorius: Rezonansas – atsiranda, kai priverstinių virpesių dažnis sutampa su natūralių virpesių dažniu (p = k). Dažniausiai tai atsitinka paleidžiant ir sustabdant blogai subalansuotų rotorių, pritvirtintų prie elastinių pakabų, sukimąsi. Vienodo dažnio virpesių diferencialinė lygtis: konkretus sprendimas dešiniosios pusės pavidalu negali būti priimtas, nes gausite tiesiškai priklausomą sprendimą (žr. bendrąjį sprendimą). Bendras sprendimas: Pakeisti diferencialinėje lygtyje: Paimkite konkretų sprendinį formoje ir apskaičiuokite išvestines: Taigi gaunamas sprendimas: arba Priverstiniai svyravimai esant rezonansui turi amplitudę, kuri proporcingai laikui didėja neribotai. Atsparumo judėjimui poveikis priverstinės vibracijos metu. Diferencialinė lygtis esant klampiam atsparumui turi tokią formą: Bendrasis sprendimas parenkamas iš lentelės (3 paskaita, 11 psl.), priklausomai nuo n ir k santykio (žr.). Paimame konkretų sprendinį formoje ir apskaičiuojame išvestines: Pakeiskite diferencialinėje lygtyje: Sulyginus tų pačių trigonometrinių funkcijų koeficientus, gauname lygčių sistemą: Abi lygtis pakeliant į laipsnį ir pridedant jas prie abiejų lygčių laipsnio. , gauname priverstinių virpesių amplitudę: Antrąją lygtį padalijus iš pirmosios, gauname priverstinių svyravimų fazinį poslinkį: Taigi , judesio lygtis priverstiniams virpesiams, atsižvelgiant į pasipriešinimą judėjimui, pvz. už n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 skaidrė

5 paskaita Materialaus taško santykinis judėjimas – Tarkime, kad judanti (neinercinė) koordinačių sistema Oxyz juda pagal tam tikrą dėsnį stacionarios (inercinės) koordinačių sistemos O1x1y1z1 atžvilgiu. Materialaus taško M (x, y, z) judėjimas judančios sistemos Oxyz atžvilgiu santykinis, stacionarios sistemos O1x1y1z1 atžvilgiu absoliutus. Mobiliosios sistemos Oxyz judėjimas stacionarios sistemos O1x1y1z1 atžvilgiu yra nešiojamasis judesys. 14 z x1 y1 z1 O1 xy M xyz O Pagrindinė dinamikos lygtis: Absoliutus taško pagreitis: Pakeiskite absoliutųjį taško pagreitį į pagrindinę dinamikos lygtį: Perkelkite terminus su transliaciniu ir Koriolio pagreičiu į dešinę: Perkeltus terminus turi jėgų matmenis ir yra laikomos atitinkamomis inercijos jėgomis, lygiomis: Tada santykinis taško judėjimas gali būti laikomas absoliučiu, jei prie veikiančių jėgų pridėsime transliacines ir Koriolio inercijos jėgas: Ašies projekcijose judančios koordinačių sistemos, turime: sukimasis tolygus, tada εe = 0: 2. Transliacinis kreivinis judėjimas: Jei judėjimas yra tiesus, tai =: Jei judėjimas yra tiesus ir tolygus, tai judanti sistema yra inercinė, o santykinis judėjimas gali būti laikomas absoliučiu: judėjimas (klasikinės mechanikos reliatyvumo principas). Žemės sukimosi įtaka kūnų pusiausvyrai – Tarkime, kad kūnas yra pusiausvyroje ant Žemės paviršiaus savavališkoje platumoje φ (lygiagrečioje). Žemė sukasi apie savo ašį iš vakarų į rytus kampiniu greičiu: Žemės spindulys yra apie 6370 km. S R – pilna nelygaus paviršiaus reakcija. G – Žemės traukos jėga į centrą. Ф - išcentrinė inercijos jėga. Santykinės pusiausvyros sąlyga: Traukos ir inercijos jėgų rezultatas yra gravitacijos jėga (svoris): Žemės paviršiaus gravitacijos jėgos (svorio) dydis P = mg. Išcentrinė inercijos jėga yra nedidelė gravitacijos jėgos dalis: Sunkio jėgos nuokrypis nuo gravitacijos jėgos krypties taip pat mažas: Taigi Žemės sukimosi įtaka kūnų pusiausvyrai yra labai mažas ir į jį neatsižvelgiama atliekant praktinius skaičiavimus. Didžiausia inercijos jėgos vertė (esant φ = 0 - ties pusiauju) yra tik 0,00343 sunkio jėgos vertės.

17 skaidrė

5 paskaita (tęsinys 5.2) 15 Žemės sukimosi įtaka kūnų judėjimui Žemės gravitaciniame lauke – Padėkime, kad kūnas krinta į Žemę iš tam tikro aukščio H virš Žemės paviršiaus platumoje φ. Pasirinkime judantį atskaitos rėmą, standžiai sujungtą su Žeme, nukreipiant x ir y ašis liestine į lygiagretę ir į dienovidinį: Taigi gravitacijos jėga tapatinama su gravitacijos jėga. Be to, manome, kad gravitacijos jėga yra nukreipta statmenai Žemės paviršiui dėl mažo jos įlinkio, kaip aptarta aukščiau. Koriolio pagreitis yra lygus ir nukreiptas lygiagrečiai y ašiai į vakarus. Koriolio inercinė jėga yra lygi priešingos krypties. Suprojektuokime santykinio judėjimo lygtį ašyje: Pirmosios lygties sprendinys duoda: Pradinės sąlygos: Trečiosios lygties sprendinys duoda: Pradinės sąlygos: Trečioji lygtis įgauna formą: Pradinės sąlygos: Jos sprendimas duoda: Gautas sprendinys rodo, kad krintant kūnas nukrypsta į rytus. Apskaičiuokime šio nuokrypio dydį, pavyzdžiui, krintant iš 100 m aukščio Kritimo laikas randamas iš antrosios lygties sprendinio: Taigi Žemės sukimosi įtaka kūnų judėjimui labai mažas praktiniam aukščiui ir greičiams ir į jį neatsižvelgiama atliekant techninius skaičiavimus. Antrosios lygties sprendimas taip pat reiškia, kad išilgai y ašies yra greitis, kuris taip pat turėtų sukelti ir sukelti atitinkamą pagreitį ir Koriolio inercinę jėgą. Šio greičio ir su juo susijusios inercijos jėgos įtaka judesio pokyčiui bus net mažesnė už nagrinėjamą Koriolio inercinę jėgą, susijusią su vertikaliu greičiu.

18 skaidrė

6 paskaita Mechaninės sistemos dinamika. Materialių taškų sistema arba mechaninė sistema – materialių taškų arba materialių taškų rinkinys, kurį vienija bendrieji sąveikos dėsniai (kiekvieno taško arba kūno padėtis arba judėjimas priklauso nuo visų kitų padėties ir judėjimo) Sistema laisvųjų taškų – kurių judėjimo neriboja jokie ryšiai (pavyzdžiui, planetų sistema, kurioje planetos laikomos materialiais taškais). Nelaisvų taškų sistema arba nelaisva mechaninė sistema – materialių taškų ar kūnų judėjimas yra ribojamas sistemai taikomų suvaržymų (pavyzdžiui, mechanizmo, mašinos ir pan.). 16 Sistemą veikiančios jėgos. Be anksčiau buvusios jėgų klasifikacijos (aktyviosios ir reaktyviosios jėgos), įvedama nauja jėgų klasifikacija: 1. Išorinės jėgos (e) – veikiančios sistemos taškus ir kūnus iš taškų ar kūnų, kurie nėra šios sistemos dalis. sistema. 2. Vidinės jėgos (i) – sąveikos jėgos tarp materialių taškų arba kūnų, įtrauktų į šią sistemą. Viena ir ta pati jėga gali būti išorinė ir vidinė jėga. Viskas priklauso nuo to, kokia mechaninė sistema svarstoma. Pavyzdžiui: Saulės, Žemės ir Mėnulio sistemoje visos gravitacinės jėgos tarp jų yra vidinės. Nagrinėjant sistemą Žemė ir Mėnulis, Saulės veikiančios gravitacinės jėgos yra išorinės: C З Л Remiantis veikimo ir reakcijos dėsniu, kiekviena vidinė jėga Fk atitinka kitą vidinę jėgą Fk ', kurios dydis yra lygus ir priešingas. kryptis. Iš to išplaukia dvi nepaprastos vidinių jėgų savybės: Pagrindinis visų sistemos vidinių jėgų vektorius lygus nuliui: Pagrindinis visų sistemos vidinių jėgų momentas bet kurio centro atžvilgiu lygus nuliui: Arba projekcijose į koordinatę ašys: Pastaba. Nors šios lygtys yra panašios į pusiausvyros lygtis, jos nėra, nes vidinės jėgos veikia įvairius sistemos taškus ar kūnus ir gali sukelti šių taškų (kūnų) judėjimą vienas kito atžvilgiu. Iš šių lygčių matyti, kad vidinės jėgos neturi įtakos visos sistemos judėjimui. Materialiųjų taškų sistemos masės centras. Norint apibūdinti visos sistemos judėjimą, įvedamas geometrinis taškas, vadinamas masės centru, kurio spindulio vektorius nustatomas pagal išraišką, kur M yra visos sistemos masė: arba projekcijose į koordinatę ašys: masės centro formulės yra panašios į svorio centro formules. Tačiau masės centro samprata yra bendresnė, nes ji nesusijusi su gravitacijos jėgomis ar gravitacijos jėgomis.

19 skaidrė

6 paskaita (tęsinys 6.2) 17 Teorema apie sistemos masės centro judėjimą - Nagrinėkime n materialių taškų sistemą. Kiekvienam taškui taikomas jėgas padalijame į išorines ir vidines ir pakeičiame jas atitinkamais rezultantais Fke ir Fki. Užrašykime kiekvienam taškui pagrindinę dinamikos lygtį: arba Susukite šias lygtis visuose taškuose: Kairėje lygties pusėje įvedame mases išvestinės ženklu ir išvestinių sumą pakeisime išvestine suma: Iš masės centro apibrėžimo: Pakeisti gautoje lygtyje: Pašalinus sistemos masę už išvestinės ženklo ribų gauname arba: Sistemos masės ir jos centro pagreičio sandaugą, masė lygi pagrindiniam išorinių jėgų vektoriui. Projekcijose ant koordinačių ašių: Sistemos masės centras juda kaip materialus taškas, kurio masė lygi visos sistemos masei, kuriam taikomos visos sistemą veikiančios išorinės jėgos. Sistemos masės centro judėjimo teoremos padariniai (išlikimo dėsniai): 1. Jei laiko intervale pagrindinis sistemos išorinių jėgų vektorius lygus nuliui, Re = 0, tai greitis masės centras pastovus, vC = const (masės centras juda tolygiai tiesia linija – judėjimo masės centro likimo dėsnis). 2. Jei laiko intervale pagrindinio sistemos išorinių jėgų vektoriaus projekcija x ašyje lygi nuliui, Rxe = 0, tai masės centro greitis išilgai x ašies yra pastovus, vCx = const (masės centras tolygiai juda išilgai ašies). Panašūs teiginiai galioja y ir z ašims. Pavyzdys: du žmonės, kurių masė yra m1 ir m2, yra m3 masės valtyje. Iš pradžių valtis su žmonėmis ilsėjosi. Nustatykite valties judėjimą, jei žmogus, sveriantis m2, pajudėjo į valties pirmagalį atstumu a. 3. Jei laiko intervale pagrindinis sistemos išorinių jėgų vektorius lygus nuliui, Re = 0, o pradiniu momentu masės centro greitis lygus nuliui, vC = 0, tai spindulio vektorius masės centras išlieka pastovus, rC = const (masės centras yra ramybės būsenoje – masės centro padėties išsaugojimo dėsnis). 4. Jei laiko intervale pagrindinio sistemos išorinių jėgų vektoriaus projekcija į x ašį lygi nuliui, Rxe = 0, o pradiniu momentu masės centro greitis išilgai šios ašies yra lygus iki nulio, vCx = 0, tada masės centro koordinatė išilgai x ašies išlieka pastovi, xC = const (masės centras išilgai šios ašies nejuda). Panašūs teiginiai galioja y ir z ašims. 1. Judėjimo objektas (valtis su žmonėmis): 2. Išmetame jungtis (vanduo): 3. Jungtį pakeičiame reakcija: 4. Sudedame aktyviąsias jėgas: 5. Užsirašykite teoremą apie masės centrą: Projektuokite ant x ašis: O Nustatykite, kiek reikia pakeisti sėdynę m1 masės žmogui, kad valtis liktų vietoje: Valtis judės atstumu l priešinga kryptimi.

20 skaidrė

7 paskaita Jėgos impulsas - mechaninės sąveikos matas, apibūdinantis mechaninio judėjimo perdavimą iš tašką veikiančių jėgų per tam tikrą laikotarpį: 18 į jėgų tašką per tą patį laiko intervalą: Padauginkite iš dt: Integruosime per tam tikrą laiko intervalą: Taško judėjimo dydis yra mechaninio judėjimo matas, nustatomas vektoriumi, lygiu taško masės sandaugai iš jo greičio vektoriaus: sistemos judesio kiekis – Apsvarstykite sistemos n materialių taškų. Kiekvienam taškui taikomas jėgas padalijame į išorines ir vidines ir pakeičiame jas atitinkamais rezultantais Fke ir Fki. Užrašykime kiekvienam taškui pagrindinę dinamikos lygtį: arba Materialių taškų sistemos judėjimo dydis yra materialių taškų judėjimo dydžių geometrinė suma: Pagal masės centro apibrėžimą: Impulso vektorius sistemos masė yra lygi visos sistemos masės sandaugai iš sistemos masės centro greičio vektoriaus. Tada: Projekcijose ant koordinačių ašių: Sistemos impulso vektoriaus išvestinė laiko atžvilgiu lygi pagrindiniam sistemos išorinių jėgų vektoriui. Apibendrinkime šias lygtis visuose taškuose: Kairėje lygties pusėje įvedame mases po išvestinės ženklu ir išvestinių sumą pakeičiame sumos išvestine: Iš impulso impulso apibrėžimo. sistema: projekcijose į koordinačių ašis:

21 skaidrė

Eulerio teorema – Teoremos apie sistemos impulso kitimą taikymas nuolatinės terpės (vandens) judėjimui. 1. Judėjimo objektu pasirenkame vandens tūrį kreiviniame turbinos kanale: 2. Suvaržymus atmetame ir jų veikimą pakeičiame reakcijomis (Rпов – paviršiaus jėgų rezultatas) 3. Sudedame aktyviąsias jėgas (Rпов – rezultatas). tūrinių jėgų): 4. Užrašykite teoremą apie sistemos impulso kitimą: Vandens judėjimo kiekis momentais t0 ir t1 vaizduojamas kaip sumos: Vandens judėjimo kiekio pokytis laiko intervale: Vandens judėjimo kiekio pokytis per be galo mažą laiko intervalą dt:, kur F1 F2 Paėmę tankio, skerspjūvio ploto ir greičio sandaugą antrajai masei gauname: Sistemos impulsų skirtumą pakeičiant į keitimo teorema, gauname: Sistemos impulso kitimo (ištvermės dėsnių) teoremos pasekmes: 1. Jei laiko intervale pagrindinis sistemos išorinių jėgų vektorius lygus nuliui, Re = 0, tada judėjimo kiekio vektorius yra pastovus, Q = const yra sistemos impulso išsaugojimo dėsnis). 2. Jei laiko intervale pagrindinės sistemos išorinių jėgų vektoriaus projekcija x ašyje lygi nuliui, Rxe = 0, tai sistemos impulso projekcija x ašyje yra pastovi, Qx = konst. Panašūs teiginiai galioja y ir z ašims. 7 paskaita (tęsinys 7.2) Pavyzdys: M masės granata, skridusi v greičiu, sprogo į dvi dalis. Vieno iš masės m1 fragmentų greitis judėjimo kryptimi padidėjo iki reikšmės v1. Nustatykite antrosios skeveldros greitį. 1. Judėjimo objektas (granata): 2. Objektas yra laisva sistema, jungčių ir jų reakcijų nėra. 3. Sudėkite aktyviąsias jėgas: 4. Užrašykite teoremą apie impulso pokytį: Projektuokite ašyje: β Atskirkite kintamuosius ir integruokite: Dešinysis integralas praktiškai lygus nuliui, nes sprogimo laikas t

22 skaidrė

7 paskaita (tęsinys 7.3) 20 Taško kampinis impulsas arba kampinis judesio momentas tam tikro centro atžvilgiu yra mechaninio judėjimo matas, nustatomas vektoriumi, lygiu materialaus taško spindulio vektoriaus sandaugai pagal jo impulso vektorius: Materialių taškų sistemos kinetinis momentas tam tikro centro atžvilgiu yra geometrinis visų materialių taškų judesių skaičiaus to paties centro atžvilgiu momentų suma: Ašies projekcijose: Projekcijose ašis: Teorema apie sistemos kampinio momento pokytį – Nagrinėkime n materialių taškų sistemą. Kiekvienam taškui taikomas jėgas padalijame į išorines ir vidines ir pakeičiame jas atitinkamais rezultantais Fke ir Fki. Užrašykime kiekvienam taškui pagrindinę dinamikos lygtį: arba Sumuokite šias lygtis per visus taškus: Išvestinių sumą pakeiskite sumos išvestine: Išraiška skliausteliuose yra sistemos impulso momento momentas. Iš čia: Kiekvieną lygčių vektorių padauginame iš spindulio vektoriaus kairėje: Pažiūrėkime, ar galima išvestinės ženklą perkelti už vektorinio sandaugos: Taigi gavome: Kampinio momento vektoriaus išvestinė sistemos tam tikro centro atžvilgiu yra lygus pagrindiniam sistemos išorinių jėgų momentui to paties centro atžvilgiu. Projekcijose ant koordinačių ašių: Sistemos kampinio momento tam tikros ašies atžvilgiu išvestinė laike yra lygi pagrindiniam sistemos išorinių jėgų momentui tos pačios ašies atžvilgiu.

23 skaidrė

8 paskaita 21 ■ Sistemos kampinio momento kitimo teoremos padariniai (ištvermės dėsniai): 1. Jei laiko intervale sistemos išorinių jėgų pagrindinio momento vektorius kurio nors centro atžvilgiu yra lygus. iki nulio, MOe = 0, tada sistemos kampinio momento vektorius tos pačios centro konstantos atžvilgiu, KO = const yra sistemos kampinio momento išsaugojimo dėsnis). 2. Jei laiko intervale pagrindinis sistemos išorinių jėgų momentas x ašies atžvilgiu lygus nuliui, Mxe = 0, tai sistemos kampinis momentas x ašies atžvilgiu yra pastovus, Kx = const. Panašūs teiginiai galioja y ir z ašims. 2. Standaus kūno inercijos apie ašį momentas: Materialaus taško inercijos apie ašį momentas lygus taško masės sandaugai iš taško atstumo iki ašies kvadrato. Standaus kūno inercijos momentas apie ašį yra lygus kiekvieno taško masės sandaugų sumai iš šio taško atstumo iki ašies kvadrato. ■ Inercijos momentų teorijos elementai – kai sukasi standus kūnas, inercijos (atsparumo judėjimo pokyčiams) matas yra inercijos momentas apie sukimosi ašį. Panagrinėkime pagrindines apibrėžimo sąvokas ir inercijos momentų skaičiavimo metodus. 1. Materialaus taško inercijos apie ašį momentas: pereinant nuo diskrečios mažos masės į be galo mažą taško masę, tokios sumos ribą lemia integralas: standaus kūno ašinis inercijos momentas. . Be standaus kūno ašinio inercijos momento, yra ir kitų rūšių inercijos momentų: standaus kūno išcentrinis inercijos momentas. standaus kūno poliarinis inercijos momentas. 3. Teorema apie standaus kūno inercijos momentus apie lygiagrečias ašis - perėjimo į lygiagrečias ašis formulė: Inercijos momentas apie pradinę ašį Statiniai inercijos momentai apie pradines ašis Kūno masė Atstumas tarp ašių z1 ir z2 Taigi: jei ašis z1 eina per masės centrą, tada statiniai momentai lygūs nuliui:

24 skaidrė

8 paskaita (tęsinys 8.2) 22 Vienalyčio pastovaus skerspjūvio strypo inercijos momentas apie ašį: xz L Parinkime elementarų tūrį dV = Adx atstumu x: x dx Elemento masė: Apskaičiuoti inercijos momentą apie centrinę ašį (einančią per svorio centrą), pakanka pakeisti ašies padėtį ir nustatyti integravimo ribas (-L / 2, L / 2). Čia pademonstruosime perėjimo prie lygiagrečių ašių formulę: zС 5. Vienarūšio kieto cilindro inercijos momentas apie simetrijos ašį: H dr r Parinkime elementarų tūrį dV = 2πrdrH (plonas cilindras, kurio spindulys r): Elementari masė: čia naudojome cilindro tūrio formulę V = πR2H. Tuščiavidurio (storo) cilindro inercijos momentui apskaičiuoti pakanka nustatyti integravimo ribas nuo R1 iki R2 (R2> R1): 6. Plono cilindro inercijos momentas apie simetrijos ašį (t

25 skaidrė

8 paskaita (tęsinys 8.3) 23 ■ Standaus kūno sukimosi apie ašį diferencialinė lygtis: Parašykime teoremą apie standaus kūno, besisukančio apie fiksuotą ašį, kampinio momento kitimą: Sukamojo standaus kūno kinetinis momentas kūnas yra: Išorinių jėgų aplink sukimosi ašį momentas yra lygus sukimo momentui (reakcijos ir jėgos nėra momento gravitacija): Pakeiskite kampinį impulsą ir sukimo momentą teoremoje Pavyzdys: Du vienodo svorio žmonės G1 = G2 kabo. virvė, permesta per tvirtą bloką, kurio svoris G3 = G1 / 4. Kažkuriuo momentu vienas iš jų santykiniu greičiu u pradėjo lipti lynu. Nustatykite kiekvieno žmogaus kėlimo greitį. 1. Pasirinkite judėjimo objektą (blokas su žmonėmis): 2. Išmeskite jungtis (bloko atraminis įtaisas): 3. Pakeiskite jungtį reakcijomis (guoliu): 4. Pridėkite aktyvias jėgas (gravitacija): 5. Rašykite žemyn teorema apie sistemos kinetinio momento kitimą bloko sukimosi ašių atžvilgiu: R Kadangi išorinių jėgų momentas lygus nuliui, kampinis momentas turi išlikti pastovus: Pradiniu laiko momentu t = 0, buvo pusiausvyra ir Kz0 = 0. Prasidėjus vieno žmogaus judėjimui virvės atžvilgiu, pradėjo judėti visa sistema, tačiau kampinio momento sistema turi likti lygi nuliui: Kz = 0. Kinetinis momentas sistemos yra abiejų žmonių ir bloko kinetinių momentų suma: Čia v2 yra antrojo asmens greitis, lygus kabelio greičiui, Pavyzdys: Nustatykite vienalyčio masės strypo mažų laisvųjų virpesių periodą. M ir ilgis l, vienu galu pakabintas prie fiksuotos sukimosi ašies. Arba: Esant mažiems virpesiams sinφ φ: Virpesių periodas: Strypo inercijos momentas:

26 skaidrė

8 paskaita (tęsinys 8.4 – papildoma medžiaga) 24 ■ Elementari giroskopo teorija: Giroskopas – tai apie medžiagos simetrijos ašį besisukantis standus kūnas, kurio vienas iš taškų yra nejudantis. Laisvasis giroskopas fiksuojamas taip, kad jo masės centras išliktų nejudantis, o sukimosi ašis eina per masės centrą ir gali užimti bet kokią padėtį erdvėje, t.y. sukimosi ašis keičia savo padėtį kaip ir savo kūno sukimosi ašis sferinio judėjimo metu. Pagrindinė apytikslės (elementariosios) giroskopo teorijos prielaida yra ta, kad manoma, kad rotoriaus kampinio momento (kampinio momento) vektorius yra nukreiptas išilgai savo sukimosi ašies. Taigi, nepaisant to, kad bendruoju atveju rotorius dalyvauja trijuose apsisukimuose, atsižvelgiama tik į jo paties sukimosi kampinį greitį ω = dφ / dt. Taip yra dėl to, kad šiuolaikinėse technologijose giroskopo rotorius sukasi maždaug 5000–8000 rad/s kampiniu greičiu (apie 50 000–80000 aps./min.), o kiti du kampiniai greičiai yra susiję su jo precesija ir nutacija. savo sukimosi ašį dešimtis tūkstančių kartų mažesnė už šį greitį. Pagrindinė laisvojo giroskopo savybė yra ta, kad rotoriaus ašis išlaiko pastovią kryptį erdvėje inercinės (žvaigždinės) atskaitos sistemos atžvilgiu (tai rodo Foucault švytuoklė, kuri išlaiko svyravimo plokštumą žvaigždžių atžvilgiu nepakitusią, 1852). Tai išplaukia iš kampinio momento, palyginti su rotoriaus masės centru, išsaugojimo įstatymo, su sąlyga, kad nepaisoma trinties rotoriaus pakabos ašių, išorinių ir vidinių rėmų guoliuose: Jėgos poveikis laisvojo giroskopo ašiai. Esant jėgai, veikiančiai rotoriaus ašį, išorinių jėgų momentas masės centro atžvilgiu nėra lygus nuliui: jėga, o šios jėgos momento vektoriaus kryptimi, t.y. pasisuks ne apie x ašį (vidinė pakaba), o apie y ašį (išorinė pakaba). Nutraukus jėgą, rotoriaus ašis išliks nepakitusioje padėtyje, atitinkančioje paskutinį jėgos veikimo momentą, nes nuo šio laiko momento išorinių jėgų momentas vėl tampa lygus nuliui. Trumpalaikio jėgos veikimo (smūgio) atveju giroskopo ašis praktiškai nekeičia savo padėties. Taigi greitas rotoriaus sukimasis suteikia giroskopui galimybę atremti atsitiktines įtakas, linkusias keisti rotoriaus sukimosi ašies padėtį, o nuolat veikiant jėgai išlaiko plokštumos padėtį, statmeną veikiančiai jėgai. kurioje yra rotoriaus ašis. Šios savybės naudojamos eksploatuojant inercines navigacijos sistemas.

Bet kuriame akademiniame kurse fizikos studijos prasideda nuo mechanikos. Ne su teorine, ne su taikomąja ir ne su skaičiavimo, o su sena gera klasikine mechanika. Ši mechanika dar vadinama Niutono mechanika. Pasak legendos, mokslininkas vaikščiojo sode, pamatė nukritusį obuolį, ir būtent šis reiškinys pastūmėjo jį atrasti visuotinės gravitacijos dėsnį. Žinoma, įstatymas egzistavo visada, o Niutonas suteikė jam tik žmonėms suprantamą formą, tačiau jo nuopelnas neįkainojamas. Šiame straipsnyje mes neaprašysime Niutono mechanikos dėsnių kiek įmanoma išsamiau, tačiau pateiksime pagrindus, pagrindines žinias, apibrėžimus ir formules, kurios visada gali būti jūsų rankose.

Mechanika – fizikos šaka, mokslas, tiriantis materialių kūnų judėjimą ir jų tarpusavio sąveikas.

Pats žodis yra graikų kilmės ir verčiamas kaip „mašinų kūrimo menas“. Tačiau iki mašinų konstravimo mes vis dar esame kaip Mėnulis, todėl eisime protėvių pėdomis ir tyrinėsime kampu į horizontą metamų akmenų judėjimą, iš aukščio ant galvų krentančių obuolių judėjimą. h.

Kodėl fizikos studijos prasideda nuo mechanikos? Nes tai visiškai natūralu, nepradėti to nuo termodinaminės pusiausvyros?!

Mechanika yra vienas seniausių mokslų, o istoriškai fizikos studijos prasidėjo būtent nuo mechanikos pagrindų. Atsidūrę laiko ir erdvės rėmuose, žmonės iš tikrųjų negalėjo pradėti nuo kažko kito, su visu savo troškimu. Judantys kūnai yra pirmas dalykas, į kurį atkreipiame dėmesį.

Kas yra judėjimas?

Mechaninis judėjimas – tai kūnų padėties erdvėje pasikeitimas vienas kito atžvilgiu laikui bėgant.

Po šio apibrėžimo visiškai natūraliai pasiekiame atskaitos sistemos sąvoką. Kūnų padėties erdvėje keitimas vienas kito atžvilgiu. Pagrindiniai žodžiai čia: vienas kito atžvilgiu ... Juk keleivis automobilyje tam tikru greičiu juda kelio pusėje stovinčio žmogaus atžvilgiu ir atsiremia į šalia esančios sėdynės kaimyną, o kitokiu greičiu juda keleivio atžvilgiu. juos lenkiantis automobilis.

Štai kodėl, norint normaliai išmatuoti judančių objektų parametrus ir nesusipainioti, mums reikia atskaitos sistema – standžiai tarpusavyje sujungtas atskaitos kūnas, koordinačių sistema ir laikrodis. Pavyzdžiui, žemė sukasi aplink saulę heliocentrine atskaitos sistema. Kasdieniame gyvenime beveik visus matavimus atliekame geocentrinėje atskaitos sistemoje, susietoje su Žeme. Žemė yra atskaitos kūnas, kurio atžvilgiu juda automobiliai, lėktuvai, žmonės, gyvūnai.

Mechanika, kaip mokslas, turi savo užduotį. Mechanikos uždavinys – bet kuriuo metu žinoti kūno padėtį erdvėje. Kitaip tariant, mechanika sukuria matematinį judėjimo aprašymą ir randa ryšius tarp jį apibūdinančių fizikinių dydžių.

Kad galėtume judėti toliau, mums reikia koncepcijos " materialus taškas “. Jie sako, kad fizika yra tikslus mokslas, tačiau fizikai žino, kiek reikia padaryti apytikslių ir prielaidų, kad susitartų dėl šio tikslumo. Niekas niekada nematė materialaus taško ar užuodė idealias dujas, bet jie yra! Tiesiog su jais gyventi daug lengviau.

Materialus taškas yra kūnas, kurio dydis ir forma šios problemos kontekste gali būti nepaisoma.

Klasikinės mechanikos skyriai

Mechanika susideda iš kelių skyrių

• Kinematika
• Dinamika
• Statika

Kinematika fiziniu požiūriu jis tiksliai tiria, kaip kūnas juda. Kitaip tariant, šiame skyriuje nagrinėjamos kiekybinės judėjimo charakteristikos. Raskite greitį, kelią – tipines kinematines problemas

Dinamika išsprendžia klausimą, kodėl taip juda. Tai reiškia, kad atsižvelgiama į kūną veikiančias jėgas.

Statika tiria kūnų pusiausvyrą veikiant jėgoms, tai yra atsako į klausimą: kodėl ji visai nekrenta?

Klasikinės mechanikos pritaikymo ribos

Klasikinė mechanika nebepretenduoja į viską aiškinantį mokslą (praėjusio amžiaus pradžioje viskas buvo visiškai kitaip), turinčiu aiškius pritaikomumo rėmus. Apskritai, klasikinės mechanikos dėsniai galioja pasauliui, prie kurio esame įpratę pagal dydį (makrokosmosą). Jie nustoja veikti dalelių pasaulio atveju, kai kvantinė mechanika pakeičia klasikinę. Taip pat klasikinė mechanika netaikytina tais atvejais, kai kūnų judėjimas vyksta greičiu, artimu šviesos greičiui. Tokiais atvejais išryškėja reliatyvistiniai efektai. Grubiai tariant, kvantinės ir reliatyvistinės mechanikos – klasikinės mechanikos rėmuose tai ypatingas atvejis, kai kūno matmenys dideli, o greitis mažas.

Paprastai tariant, kvantiniai ir reliatyvistiniai efektai niekada niekur nedingsta, jie taip pat vyksta įprastam makroskopinių kūnų judėjimui, kurio greitis yra daug mažesnis už šviesos greitį. Kitas dalykas yra tai, kad šių efektų poveikis yra toks mažas, kad jis neviršija tiksliausių matavimų. Taigi klasikinė mechanika niekada nepraras savo esminės svarbos.

Mes ir toliau nagrinėsime fizinius mechanikos pagrindus būsimuose straipsniuose. Norėdami geriau suprasti mechaniką, visada galite kreiptis į mūsų autoriams kurie individualiai nušviečia tamsią sunkiausios užduoties vietą.

Teorinė mechanika- tai mechanikos skyrius, kuriame išdėstyti pagrindiniai mechaninio judėjimo ir medžiagų kūnų mechaninės sąveikos dėsniai.

Teorinė mechanika yra mokslas, kuriame tiriami kūnų judėjimai laikui bėgant (mechaniniai judesiai). Jis yra kitų mechanikos šakų (tamprumo teorija, medžiagų atsparumas, plastiškumo teorija, mechanizmų ir mašinų teorija, hidroaerodinamika) ir daugelio techninių disciplinų pagrindas.

Mechaninis judėjimas- tai materialių kūnų santykinės padėties erdvėje pasikeitimas laikui bėgant.

Mechaninė sąveika- tai tokia sąveika, dėl kurios pasikeičia mechaninis judėjimas arba keičiasi santykinė kūno dalių padėtis.

Tvirta kėbulo statika

Statika- tai teorinės mechanikos skyrius, kuriame nagrinėjamos standžiųjų kūnų pusiausvyros ir vienos jėgų sistemos transformavimo į kitą, jai lygiavertę, problemas.

Pagrindinės statikos sąvokos ir dėsniai
• Visiškai solidus(kietas, kūnas) yra materialus kūnas, atstumas tarp bet kurių taškų, kuriame nekinta.
• Materialinis taškas Ar kūnas, kurio matmenys, atsižvelgiant į problemos sąlygas, gali būti nepaisomi.
• Laisvas kūnas Ar kūnas, kurio judėjimui netaikomi jokie apribojimai.
• Nelaisvas (surištas) kūnas Ar kūnas, kurio judėjimui taikomi apribojimai.
• Jungtys- tai kūnai, neleidžiantys nagrinėjamam objektui (kūnui ar kūnų sistemai) judėti.
• Bendravimo reakcija Tai jėga, apibūdinanti jungties poveikį standžiam kūnui. Jei jėgą, kuria standus kūnas veikia ryšį, laikysime veiksmu, tada ryšio reakcija yra reakcija. Šiuo atveju jėga – veiksmas taikomas ryšiui, o ryšio reakcija – kietajai medžiagai.
• Mechaninė sistema Yra tarpusavyje susijusių kūnų arba materialių taškų rinkinys.
• Tvirtas galima laikyti mechanine sistema, kurios padėtis ir atstumas tarp taškų nesikeičia.
• Jėga Tai vektorinis dydis, apibūdinantis mechaninį vieno materialaus kūno poveikį kitam.
  Jėgai kaip vektoriui būdingas taikymo taškas, veikimo kryptis ir absoliuti reikšmė. Jėgos modulio matavimo vienetas yra Niutonas.
• Jėgos veiksmų linija Tai tiesi linija, iš kurios nukreiptas jėgos vektorius.
• Koncentruota galia- jėga, taikoma viename taške.
• Paskirstytos jėgos (paskirstyta apkrova)– tai jėgos, veikiančios visus kūno tūrio, paviršiaus ar ilgio taškus.
  Paskirstyta apkrova nustatoma jėga, veikiančia tūrio vienetą (paviršius, ilgis).
  Paskirstytos apkrovos matmenys yra N / m 3 (N / m 2, N / m).
• Išorinė jėga Tai jėga, veikianti iš kūno, nepriklausančio nagrinėjamai mechaninei sistemai.
• Vidinė stiprybė Ar jėga, veikianti materialų mechaninės sistemos tašką iš kito materialaus taško, priklausančio nagrinėjamai sistemai.
• Jėgos sistema Ar mechaninę sistemą veikiančių jėgų visuma.
• Plokščia jėgų sistema Tai jėgų sistema, kurios veikimo linijos yra toje pačioje plokštumoje.
• Erdvinė jėgų sistema Tai jėgų sistema, kurios veikimo linijos nėra toje pačioje plokštumoje.
• Susiliejančių jėgų sistema Ar jėgų sistema, kurios veikimo linijos susikerta viename taške.
• Savavališka jėgų sistema Ar jėgų sistema, kurios veikimo linijos nesikerta viename taške.
• Lygiavertės jėgų sistemos- tai jėgų sistemos, kurias pakeitus viena kita nepakeičiama kūno mechaninė būsena.
  Priimtas pavadinimas:.
• Pusiausvyra- tai būsena, kai kūnas, veikiamas jėgų, lieka nejudantis arba tolygiai juda tiesia linija.
• Subalansuota jėgų sistema Ar jėgų sistema, kuri, veikiant laisvai kietajai medžiagai, nekeičia jo mechaninės būsenos (neišbalansuoja).
  .
• Rezultatinė jėga Tai jėga, kurios poveikis kūnui prilygsta jėgų sistemos veikimui.
  .
• Galios akimirka Tai vertė, apibūdinanti jėgos sukimosi gebėjimą.
• Pora jėgų Yra dviejų lygiagrečių, vienodo dydžio, priešingai nukreiptų jėgų sistema.
  Priimtas pavadinimas:.
  Veikiant jėgų porai, kūnas suksis.
• Ašies jėgos projekcija Ar atkarpa, uždaryta tarp statmenų, nubrėžtų nuo jėgos vektoriaus pradžios ir pabaigos iki šios ašies.
  Projekcija yra teigiama, jei linijos atkarpos kryptis sutampa su teigiama ašies kryptimi.
• Jėgos projekcija į plokštumą Ar vektorius plokštumoje, uždarytas tarp statmenų, nubrėžtų nuo jėgos vektoriaus pradžios ir pabaigos iki šios plokštumos.
• 1 dėsnis (inercijos dėsnis). Izoliuotas materialus taškas yra ramybės būsenoje arba juda tolygiai ir tiesia linija.
  Tolygus ir tiesus materialaus taško judėjimas yra judėjimas pagal inerciją. Pusiausvyros būsena tarp materialaus taško ir standaus kūno suprantama ne tik kaip ramybės būsena, bet ir kaip judėjimas inercijos dėka. Kietam kūnui yra įvairių tipų inercinis judėjimas, pavyzdžiui, tolygus standaus kūno sukimasis aplink fiksuotą ašį.
• 2 įstatymas. Tvirtas kūnas yra pusiausvyroje veikiant dviem jėgoms tik tuo atveju, jei šios jėgos yra vienodo dydžio ir nukreiptos priešingomis kryptimis išilgai bendros veikimo linijos.
  Šios dvi jėgos vadinamos balansuojančiomis jėgomis.
  Apskritai jėgos vadinamos balansavimo, jei standus kūnas, kuriam šios jėgos veikia, yra ramybės būsenoje.
• 3 įstatymas. Nepažeidžiant standaus kūno būsenos (žodis „būsena“ čia reiškia judėjimo arba ramybės būseną), galima pridėti ir nuleisti atsvarines jėgas.
  Pasekmė. Nepažeidžiant standaus kūno būsenos, jėga gali būti perkelta išilgai jos veikimo linijos į bet kurį kūno tašką.
  Dvi jėgų sistemos vadinamos lygiavertėmis, jei vieną iš jų galima pakeisti kita nepažeidžiant standaus kūno būsenos.
• 4 įstatymas. Dviejų jėgų, veikiančių viename taške, veikiančių tame pačiame taške, rezultatas yra lygus lygiagretainio, sukurto ant šių jėgų, įstrižainės ir nukreiptas išilgai
  įstrižainės.
  Rezultato modulis yra lygus:
  
• 5 įstatymas (veiksmų ir reakcijos lygybės dėsnis)... Jėgos, kuriomis du kūnai veikia vienas kitą, yra vienodo dydžio ir nukreiptos priešingomis kryptimis išilgai vienos tiesės.
  Reikėtų nepamiršti, kad veiksmas- jėga, taikoma kūnui B, ir priešprieša- jėga, taikoma kūnui A nėra subalansuoti, nes yra pritvirtinti prie skirtingų kūnų.
• 6 įstatymas (užkietėjimo įstatymas)... Kieto kūno pusiausvyra jam kietėjant nesutrinka.
  Nereikia pamiršti, kad pusiausvyros sąlygos, kurios būtinos ir pakankamos kietajai medžiagai, yra būtinos, bet nepakankamos atitinkamam nekietajam.
• 7 įstatymas (atleidimo nuo ryšių įstatymas). Nelaisvas standus kūnas gali būti laikomas laisvu, jei jis psichiškai išlaisvintas iš saitų, pakeičiant ryšių veikimą atitinkamomis ryšių reakcijomis.

Ryšiai ir jų reakcijos
• Lygus paviršius riboja judėjimą išilgai įprasto atraminio paviršiaus. Reakcija nukreipta statmenai paviršiui.
• Šarnyrinė kilnojamoji atrama riboja kūno judėjimą išilgai normalios į atskaitos plokštumą. Reakcija nukreipta išilgai normalios į atraminį paviršių.
• Šarnyrinė fiksuota atrama atsveria bet kokį judėjimą plokštumoje, statmenoje sukimosi ašiai.
• Šarnyrinis nesvarus strypas atsveria kūno judėjimą išilgai strypo linijos. Reakcija bus nukreipta išilgai juostos linijos.
• Aklas nutraukimas atsveria bet kokį judėjimą ir sukimąsi plokštumoje. Jo veikimą galima pakeisti jėga, pavaizduota dviejų komponentų pavidalu, ir jėgų pora su momentu.

Kinematika

Kinematika- teorinės mechanikos skyrius, kuriame nagrinėjamos mechaninio judėjimo, kaip erdvėje ir laike vykstančio proceso, bendrosios geometrinės savybės. Judantys objektai laikomi geometriniais taškais arba geometriniais kūnais.

Pagrindinės kinematikos sąvokos
• Taško (kūno) judėjimo dėsnis Ar taško (kūno) padėties erdvėje priklausomybė nuo laiko.
• Taško trajektorija Ar taško geometrinė padėtis erdvėje jo judėjimo metu.
• Taško (kūno) greitis- Tai taško (kūno) padėties erdvėje pokyčio laike charakteristika.
• Taško (kūno) pagreitis- Tai taško (kūno) greičio pokyčio laiko charakteristika.

Taško kinematinių charakteristikų nustatymas
• Taško trajektorija
  Vektorinėje atskaitos sistemoje trajektorija apibūdinama išraiška:.
  Atskaitos koordinačių sistemoje trajektorija nustatoma pagal taško judėjimo dėsnį ir apibūdinama išraiškomis z = f (x, y)- erdvėje arba y = f (x)- lėktuve.
  Natūralioje atskaitos sistemoje trajektorija nustatoma iš anksto.
• Taško greičio nustatymas vektorių koordinačių sistemoje
  Nurodant taško judėjimą vektorių koordinačių sistemoje, judėjimo ir laiko intervalo santykis vadinamas vidutine greičio reikšme šiame laiko intervale:.
  Laikydami laiko intervalą kaip be galo mažą reikšmę, greičio reikšmė gaunama tam tikru laiku (momentinė greičio reikšmė): .
  Vidutinio greičio vektorius nukreiptas išilgai vektoriaus taško judėjimo kryptimi, momentinio greičio vektorius nukreiptas liestinei trajektorijai taško judėjimo kryptimi.
  Išvestis: taško greitis yra vektorinis dydis, lygus judėjimo dėsnio išvestinei laiko atžvilgiu.
  Išvestinė nuosavybė: bet kokio dydžio išvestinė laiko atžvilgiu lemia šio dydžio kitimo greitį.
• Taško greičio nustatymas koordinačių sistemoje
  Taško koordinačių kitimo tempai:
  .
  Taško su stačiakampe koordinačių sistema viso greičio modulis bus lygus:
  .
  Greičio vektoriaus kryptis nustatoma pagal krypties kampų kosinusus:
  ,
  kur yra kampai tarp greičio vektoriaus ir koordinačių ašių.
• Taško greičio nustatymas natūralioje atskaitos sistemoje
  Taško greitis natūralioje atskaitos sistemoje nustatomas kaip taško judėjimo dėsnio išvestinė:.
  Remiantis ankstesnėmis išvadomis, greičio vektorius yra nukreiptas liestinės trajektorijos taško judėjimo kryptimi ir ašimis nustatomas tik vienos projekcijos.

Standžios kūno kinematika
• Kietųjų kūnų kinematikoje išsprendžiamos dvi pagrindinės užduotys:
  1) judėjimo užduotis ir viso kūno kinematinių charakteristikų nustatymas;
  2) kūno taškų kinematinių charakteristikų nustatymas.
• Standaus kūno transliacinis judėjimas
  Transliacinis judesys – tai judesys, kai tiesi linija, nubrėžta per du kūno taškus, lieka lygiagreti pradinei padėčiai.
  Teorema: Transliacinio judėjimo metu visi kūno taškai juda tomis pačiomis trajektorijomis ir kiekvienu laiko momentu turi tą patį greitį ir pagreitį pagal dydį ir kryptį.
  Išvestis: standaus kūno transliacinį judėjimą lemia bet kurio jo taško judėjimas, todėl jo judėjimo užduotis ir tyrimas redukuojamas iki taško kinematikos.
• Sukamasis standaus kūno judėjimas aplink fiksuotą ašį
  Sukamasis standaus kūno judėjimas aplink fiksuotą ašį – tai standaus kūno judėjimas, kai du kūnui priklausantys taškai lieka nejudantys per visą judėjimo laiką.
  Kūno padėtis nustatoma pagal sukimosi kampą. Kampo vienetas yra radianai. (Radianas yra apskritimo, kurio lanko ilgis lygus spinduliui, centrinis kampas, bendrame apskritimo kampe yra 2π radianais.)
  Kūno sukimosi aplink fiksuotą ašį dėsnis.
  Kūno kampinis greitis ir kampinis pagreitis nustatomi diferenciacijos metodu:
  - kampinis greitis, rad / s;
  - kampinis pagreitis, rad / s².
  Jei pjaunate kūną plokštuma, statmena ašiai, pasirinkite tašką sukimosi ašyje SU ir savavališkas taškas M tada taškas M apibūdins aplink esmę SU apskritimo spindulys R... Per dtįvyksta elementarus sukimasis kampu, o taškas M judės išilgai trajektorijos per atstumą .
  Linijinio greičio modulis:
  .
  Taško pagreitis M su žinoma trajektorija, ją lemia jos komponentai:
  ,
  kur .
  Dėl to gauname formules
  tangentinis pagreitis: ;
  normalus pagreitis: .

Dinamika

Dinamika– Tai teorinės mechanikos skyrius, kuriame tiriami mechaniniai materialių kūnų judesiai, priklausomai nuo juos sukeliančių priežasčių.

Pagrindinės dinamikos sąvokos
• Inercija- tai materialių kūnų savybė išlaikyti ramybės būseną arba tolygų tiesinį judėjimą tol, kol išorinės jėgos nepakeis šios būsenos.
• Svoris Yra kiekybinis kūno inercijos matas. Masės matavimo vienetas yra kilogramas (kg).
• Materialinis taškas Ar kūnas, turintis masę, kurio matmenys sprendžiant šią problemą nepaisomi.
• Mechaninės sistemos svorio centras- geometrinis taškas, kurio koordinatės nustatomos pagal formules:
  
  kur m k, x k, y k, z k- masė ir koordinatės k- mechaninės sistemos taškas, m Ar sistemos masė.
  Vienalyčiame gravitacijos lauke masės centro padėtis sutampa su svorio centro padėtimi.
• Materialaus kūno inercijos apie ašį momentas Yra kiekybinis inercijos matas sukimosi metu.
  Materialaus taško inercijos momentas apie ašį yra lygus taško masės sandaugai taško atstumo nuo ašies kvadratu:
  .
  Sistemos (kūno) inercijos momentas apie ašį lygus visų taškų inercijos momentų aritmetinei sumai:
  
• Materialaus taško inercijos jėga Ar vektorinis dydis yra lygus taško masės sandaugai pagal pagreičio modulį ir nukreiptas priešais pagreičio vektorių:
• Materialaus kūno inercijos jėga Ar vektorinis dydis yra lygus kūno masės sandaugai su kūno masės centro pagreičio moduliu ir nukreiptas priešingai masės centro pagreičio vektoriui:
  kur yra kūno masės centro pagreitis.
• Elementarus jėgos impulsas Ar vektorinis dydis lygus jėgos vektoriaus sandaugai be galo mažu laiko intervalu dt:
  .
  Bendras jėgos impulsas Δt yra lygus elementariųjų impulsų integralui:
  .
• Elementarus jėgos darbas Yra skaliaras dA lygus skaliariniam proi

Žiūrėti:Šis straipsnis buvo perskaitytas 32852 kartus

Pdf Pasirinkite kalbą ... Rusų Ukrainiečių Anglų

Trumpa apžvalga

Visa medžiaga atsisiunčiama aukščiau, prieš tai pasirinkus kalbą

• Statika
  • Pagrindinės statikos sąvokos
  • Jėgų rūšys
  • Statikos aksiomos
  • Ryšiai ir jų reakcijos
  • Susiliejančių jėgų sistema
    • Rezultatinės konverguojančių jėgų sistemos nustatymo metodai
    • Konverguojančių jėgų sistemos pusiausvyros sąlygos
  • Jėgos momentas centro, kaip vektoriaus, atžvilgiu
    • Jėgos momento algebrinis dydis
    • Jėgos momento apie centrą (tašką) savybės
  • Jėgų porų teorija
    • Dviejų lygiagrečių jėgų, nukreiptų viena kryptimi, sudėjimas
    • Dviejų lygiagrečių jėgų, nukreiptų priešingomis kryptimis, pridėjimas
    • Jėgų poros
    • Jėgų poros teoremos
    • Jėgų porų sistemos pusiausvyros sąlygos
  • Svirties rankena
  • Savavališka plokščia jėgų sistema
    • Plokštumos jėgų sistemos redukavimo į paprastesnę formą atvejai
    • Analitinės pusiausvyros sąlygos
  • Lygiagrečių pajėgų centras. Svorio centras
    • Lygiagrečių pajėgų centras
    • Standaus kūno svorio centras ir jo koordinatės
    • Tūrio, plokštumos ir linijos svorio centras
    • Svorio centro padėties nustatymo metodai
• Stiprumo skaičiavimo pagrindai
  • Medžiagų stiprumo užduotys ir metodai
  • Krovinių klasifikacija
  • Konstrukcinių elementų klasifikacija
  • Strypų deformacijos
  • Pagrindinės hipotezės ir principai
  • Vidinės jėgos. Pjūvio metodas
  • Įtampa
  • Tempimas ir suspaudimas
  • Medžiagos mechaninės charakteristikos
  • Leidžiamos įtampos
  • Medžiagų kietumas
  • Išilginių jėgų ir įtempių grafikai
  • Shift
  • Pjūvių geometrinės charakteristikos
  • Sukimas
  • Lenkimas
    • Diferencialinio lenkimo apribojimai
    • Lenkimo stiprumas
    • Normalios įtampos. Stiprumo skaičiavimas
    • Šlyties lenkimo įtempiai
    • Lenkimo standumas
  • Bendrosios įtempimo būsenos teorijos elementai
  • Stiprumo teorijos
  • Torsioninis lenkimas
• Kinematika
  • Taškinė kinematika
    • Taško trajektorija
    • Taško judėjimo nustatymo metodai
    • Taško greitis
    • Taško pagreitis
  • Standžios kūno kinematika
    • Standaus kūno transliacinis judėjimas
    • Sukamasis standaus kūno judėjimas
    • Pavarų kinematika
    • Plokštumai lygiagretus standaus kūno judėjimas
  • Sudėtingas taško judėjimas
• Dinamika
  • Pagrindiniai dinamikos dėsniai
  • Taško dinamika
    • Laisvo materialaus taško diferencialinės lygtys
    • Dvi taško dinamikos problemos
  • Tvirta kėbulo dinamika
    • Mechaninę sistemą veikiančių jėgų klasifikacija
    • Mechaninės sistemos judėjimo diferencialinės lygtys
  • Bendrosios dinamikos teoremos
    • Mechaninės sistemos masės centro judėjimo teorema
    • Impulso kitimo teorema
    • Kampinio momento kitimo teorema
    • Kinetinės energijos kitimo teorema
• Mašinose veikiančios jėgos
  • Jėgos, įjungiančios krumpliaratį
  • Trintis mechanizmuose ir mašinose
    • Slydimo trintis
    • Riedėjimo trintis
  • Efektyvumas
• Mašinos dalys
  • Mechaninė transmisija
    • Mechaninių transmisijų tipai
    • Pagrindiniai ir išvestiniai mechaninių pavarų parametrai
    • Pavarų transmisija
    • Lanksčios jungties perdavimai
  • Velenai
    • Paskirtis ir klasifikacija
    • Projektinis skaičiavimas
    • Patikrinkite velenų skaičiavimą
  • Guoliai
    • Paprasti guoliai
    • Riedėjimo guoliai
  • Mašinos dalių sujungimas
    • Nuimamų ir vientisų jungčių tipai
    • Sujungimai su raktais
• Normų standartizavimas, pakeičiamumas
  • Tolerancijos ir nusileidimai
  • Vieninga leistinų nuokrypių ir tūpimų sistema (ESGP)
  • Geometrinė tolerancija ir padėtis

Formatas: pdf

Dydis: 4MB

rusų kalba

Krumpliaračio skaičiavimo pavyzdys
Krumpliaračio skaičiavimo pavyzdys. Atliktas medžiagos pasirinkimas, leistinų įtempių skaičiavimas, sąlyčio ir stiprio lenkimui skaičiavimas.

Sijos lenkimo problemos sprendimo pavyzdys
Pavyzdyje sukonstruotos šlyties jėgų ir lenkimo momentų diagramos, randama pavojinga atkarpa ir parenkama I-sija. Uždavinyje analizuojama diagramų konstravimas naudojant diferencines priklausomybes, atliekama įvairių sijos skerspjūvių lyginamoji analizė.

Veleno sukimo problemos sprendimo pavyzdys
Užduotis – patikrinti plieninio veleno stiprumą tam tikram skersmeniui, medžiagai ir leistinams įtempiams. Sprendimo metu brėžiamos sukimo momentų, šlyties įtempių ir sukimo kampų diagramos. Neatsižvelgiama į veleno savo svorį.

Strypo įtempimo-suspaudimo problemos sprendimo pavyzdys
Užduotis – patikrinti plieninio strypo stiprumą esant tam tikram leistinam įtempimui. Sprendimo metu brėžiamos išilginių jėgų, normaliųjų įtempių ir poslinkių diagramos. Neatsižvelgiama į savo paties strypo svorį.

Kinetinės energijos tvermės teoremos taikymas
Mechaninės sistemos kinetinės energijos išsaugojimo teoremos taikymo problemos sprendimo pavyzdys

Taško greičio ir pagreičio nustatymas pagal pateiktas judėjimo lygtis
Uždavinio, skirto taško greičiui ir pagreičiui nustatyti pagal pateiktas judėjimo lygtis, sprendimo pavyzdys

Standaus kūno taškų greičių ir pagreičių nustatymas plokštumai lygiagrečiai judant
Standaus kūno taškų greičių ir pagreičių nustatymo plokštumai lygiagrečiai judant problemos sprendimo pavyzdys

Jėgų nustatymas plokščios santvaros strypuose
Plokščios santvaros strypų jėgų nustatymo Ritter metodu ir mazgų pjovimo metodu problemos sprendimo pavyzdys

valstybinė autonominė institucija

Kaliningrado sritis

profesionali švietimo organizacija

Paslaugų ir turizmo kolegija

Paskaitų kursas su praktinių užduočių pavyzdžiais

„Teorinės mechanikos pagrindai“

pagal disciplinąTechninė mechanika

studentams3 kursą

specialybės02/20/04 Priešgaisrinė sauga

Kaliningradas

PATVIRTINTA

UR GAU KO VET KSTN direktoriaus pavaduotojas. Myasnikova

PATVIRTINTA

GAU KO POO KST metodinė taryba

LAIKOMAS

PCC posėdyje

Redakcinė komanda:

Kolganova A.A., metodininkė

Falaleeva A.B., rusų kalbos ir literatūros mokytoja

Tsvetaeva L.V., PCC pirmininkasbendrosios matematikos ir gamtos mokslų disciplinos

Parengė:

I. V. Nezvanova GAU KO VET KST mokytojas

Turinys

1. Teorinė informacija

1. Teorinė informacija

1. Praktinių problemų sprendimo pavyzdžiai

Dinamika: pagrindinės sąvokos ir aksiomos

1. Teorinė informacija

1. Praktinių problemų sprendimo pavyzdžiai

Bibliografija

Statika: pagrindinės sąvokos ir aksiomos.

1. Teorinė informacija

Statika - teorinės mechanikos skyrius, kuriame nagrinėjamos standaus kūno taškuose veikiančių jėgų savybės ir jų pusiausvyros sąlygos. Pagrindiniai tikslai:

1. Jėgų sistemų transformacijos į lygiavertes jėgų sistemas.

2. Jėgų, veikiančių standųjį kūną, pusiausvyros sąlygų nustatymas.

Materialinis taškas vadinamas paprasčiausiu materialaus kūno modeliu

bet kokia forma, kurios matmenys yra pakankamai maži ir kurią galima paimti kaip geometrinį tašką, turintį tam tikrą masę. Bet koks materialių taškų rinkinys vadinamas mechanine sistema. Absoliučiai kietas kūnas – tai mechaninė sistema, kurios atstumai tarp taškų nesikeičia esant jokiai sąveikai.

Jėga Materialių kūnų tarpusavio sąveikos matas. Jėga yra vektorinis dydis, nes jį lemia trys elementai:

skaitinė reikšmė;

kryptis;

taikymo taškas (A).

Jėgos matavimo vienetas yra Niutonas (N).

1.1 pav

Jėgų sistema yra jėgų, veikiančių kūną, derinys.

Subalansuota (lygia nuliui) jėgų sistema vadinama sistema, kuri, pritaikyta kūnui, nekeičia jo būsenos.

Kūną veikiančią jėgų sistemą galima pakeisti viena rezultatine, veikiančia kaip jėgų sistema.

Statikos aksiomos.

1 aksioma: Jei kūnui taikoma subalansuota jėgų sistema, tai jis juda tolygiai ir tiesia linija arba yra ramybės būsenoje (inercijos dėsnis).

2 aksioma: Absoliučiai standus kūnas yra pusiausvyroje, veikiant dviem jėgoms, tada ir tik tada, kai šios jėgos yra vienodo dydžio, veikia viena tiese ir yra nukreiptos priešingomis kryptimis. 1.2 pav

3 aksioma: Kūno mechaninė būsena nebus sutrikdyta, jei prie jį veikiančių jėgų sistemos bus pridėta arba iš jos atimta subalansuota jėgų sistema.

4 aksioma: Dviejų jėgų, veikiančių kūną, rezultatas yra lygus jų geometrinei sumai, tai yra, jis išreiškiamas dydžiu ir kryptimi lygiagretainio, pastatyto ant šių jėgų kaip šonuose, įstrižainės.

1.3 pav.

5 aksioma: Jėgos, kuriomis du kūnai veikia vienas kitą, visada yra vienodo dydžio ir nukreiptos išilgai vienos tiesės priešingomis kryptimis.

1.4 pav.

Ryšių rūšys ir jų reakcijos

Nuorodos vadinami bet kokie apribojimai, trukdantys kūnui judėti erdvėje. Kūnas, veikiamas jėgų stengdamasis atlikti judesį, kuriam trukdo ryšys, veiks jį tam tikra jėga, vadinama spaudimo jėga bendravimui ... Pagal veiksmo ir reakcijos lygybės dėsnį ryšys kūną veiks tuo pačiu moduliu, bet priešingai nukreipta jėga.
Jėga, kuria šis ryšys veikia kūną, užkertant kelią vienam ar kitam judėjimui, vadinama ryšio reakcijos (reakcijos) stiprumas .
Viena iš pagrindinių mechanikos nuostatų yra obligacijų atleidimo principas : bet kuris nelaisvas kūnas gali būti laikomas laisvu, jei atsisakoma ryšių ir jų veikimas pakeičiamas ryšių reakcijomis.

Ryšio reakcija nukreipta priešinga kryptimi nei ta, kur jungtis neleidžia kūnui judėti. Pagrindinės jungčių rūšys ir jų reakcijos pateiktos 1.1 lentelėje.

1.1 lentelė

Ryšių rūšys ir jų reakcijos

Bendravimo pavadinimas

Simbolis

1

Lygus paviršius (atrama) - paviršius (atrama), trintis, ant kurios galima nepaisyti nurodyto kūno.
Su nemokama pagalba, reakcijanukreipiamas statmenai per tašką nubrėžtai liesčiaiA kūno kontaktas1 su atraminiu paviršiumi2 .

2

Siūlas (lankstus, nepratęsiamas). Sujungimas, įgyvendintas neištempto sriegio pavidalu, neleidžia kėbului atitolti nuo pakabos taško. Todėl sriegio reakcija yra nukreipta išilgai sriegio iki jo pakabos taško.

3

Nesvarus strypas - strypas, kurio svorio galima nepaisyti, palyginti su suvokiama apkrova.
Nesvario šarnyrinio tiesinio strypo reakcija nukreipta išilgai strypo ašies.

4

Judamas vyris, vyriai kilnojama atrama. Reakcija nukreipta išilgai normalios į atraminį paviršių.

7

Tvirtas nutraukimas. Standžios pabaigos plokštumoje bus du reakcijos komponentai, o jėgų poros momentaskuri neleidžia sijai pasisukti1 taško atžvilgiuA .
Tvirtas tvirtinimas erdvėje atima iš 1 kūno visus šešis laisvės laipsnius – tris poslinkius išilgai koordinačių ašių ir tris sukimus apie šias ašis.
Erdviniame standžiajame gale bus trys komponentai, , ir trys jėgų porų momentai.

Susiliejančių jėgų sistema

Susiliejančių jėgų sistema vadinama jėgų sistema, kurios veikimo linijos susikerta viename taške. Dvi jėgos, susiliejančios viename taške, pagal trečiąją statikos aksiomą gali būti pakeistos viena jėga -gaunamas .
Pagrindinis jėgų sistemos vektorius - reikšmė lygi geometrinei sistemos jėgų sumai.

Gauta plokštumos konverguojančių jėgų sistema galima nustatytigrafiškai ir analitiškai.

Jėgų sistemos papildymas . Plokščios konverguojančių jėgų sistemos sudėjimas atliekamas arba nuosekliai sudedant jėgas sukonstruojant tarpinį rezultatą (1.5 pav.), arba sukonstruojant jėgos daugiakampį (1.6 pav.).

1.5 pav. 1.6 pav

Ašies jėgos projekcija - algebrinis dydis, lygus jėgos modulio sandaugai kampo tarp jėgos ir teigiamos ašies krypties kosinuso.
ProjekcijaFx(1.7 pav.) ašies jėgos NSteigiamas, jei kampas α yra smailus, neigiamas, jei kampas α yra bukas. Jei jėgosyra statmena ašiai, tada jo projekcija į ašį lygi nuliui.

1.7 pav

Jėgos projekcija į plokštumą Oho- vektorius , uždarytas tarp jėgos pradžios ir pabaigos projekcijųį šį lėktuvą. Tie. jėgos projekcija į plokštumą yra vektorinis dydis, apibūdinamas ne tik skaitine verte, bet ir kryptimi plokštumojeOho (1.8 pav.).

1.8 pav

Tada projekcijos modulis lėktuve Oho bus lygus:

Fxy = F cosα,

čia α yra kampas tarp jėgos krypties ir jo projekcija.
Analitinis jėgų nustatymo būdas . Analitiniam stiprumo nustatymo būduibūtina pasirinkti koordinačių sistemąOhyz, kurio atžvilgiu bus nustatyta jėgos kryptis erdvėje.
Vektorius, vaizduojantis jėgą, galima nubraižyti, jei yra žinomi šios jėgos modulis ir kampai α, β, γ, kuriuos jėga sudaro su koordinačių ašimis. TaškasA jėgos taikymas nustato atskirai jo koordinatėmisNS, adresu, z... Galite nustatyti jo projekcijų stiprumąFx, Fy, Fzant koordinačių ašių. Jėgos modulis šiuo atveju nustatomas pagal formulę:

o krypties kosinusai yra:

, .

Analitinis jėgų sudėjimo būdas : sumos vektoriaus projekcija į kurią nors ašį lygi vektorių narių projekcijų toje pačioje ašyje algebrinei sumai, t.y., jei:

tada , , .
Žinant Rx, Ry, Rz, galime apibrėžti modulį

ir krypties kosinusai:

, , .

1.9 pav

Konverguojančių jėgų sistemos pusiausvyrai būtina ir pakanka, kad šių jėgų rezultantas būtų lygus nuliui.
1) Geometrinės pusiausvyros sąlyga konverguojančiai jėgų sistemai : konverguojančių jėgų sistemos pusiausvyrai būtina ir pakanka, kad galios daugiakampis, sudarytas iš šių jėgų,

buvo uždarytas (paskutinio termino vektoriaus pabaiga

jėga turi būti derinama su jėgos pirmojo nario vektoriaus pradžia). Tada pagrindinis jėgų sistemos vektorius bus lygus nuliui ()
2) Analitinės pusiausvyros sąlygos . Pagrindinio jėgų sistemos vektoriaus modulis nustatomas pagal formulę. = 0. Tiek, kiek , tada radikalioji išraiška gali būti lygi nuliui tik tuo atveju, jei kiekvienas narys vienu metu išnyksta, t.y.

Rx= 0, Ry= 0, R z = 0.

Vadinasi, susiliejančių jėgų erdvinės sistemos pusiausvyrai būtina ir pakanka, kad šių jėgų projekcijų sumos kiekvienoje iš trijų ašių koordinačių būtų lygios nuliui:

Plokščios konverguojančių jėgų sistemos pusiausvyrai būtina ir pakanka, kad jėgų projekcijų į kiekvieną iš dviejų koordinačių ašių sumos būtų lygios nuliui:

Dviejų lygiagrečių jėgų, nukreiptų viena kryptimi, pridėjimas.

1.9 pav

Dvi lygiagrečios jėgos, nukreiptos viena kryptimi, yra sumažinamos iki vienos gaunamos jėgos, lygiagrečios joms ir nukreiptos ta pačia kryptimi. Rezultato dydis yra lygus šių jėgų dydžių sumai, o jo taikymo taškas C padalija atstumą tarp jėgų veikimo linijų vidiniu būdu į dalis, atvirkščiai proporcingas šių jėgų dydžiams, tai yra

B A C

R = F 1 + F 2

Dviejų nelygių lygiagrečių jėgų, nukreiptų priešingomis kryptimis, pridėjimas.

Dvi nevienodo dydžio antilygiagrečios jėgos sumažinamos iki vienos joms lygiagrečios atsirandančios jėgos, nukreiptos į didesnę jėgą. Rezultato dydis yra lygus šių jėgų dydžių skirtumui, o jo taikymo taškas C padalija atstumą tarp išorinių jėgų veikimo linijų į dalis, atvirkščiai proporcingas šių jėgų dydžiams, yra

Jėgų pora ir jėgos momentas taško atžvilgiu.

Galios akimirka taško O atžvilgiu, paimta su atitinkamu ženklu, vadinama jėgos dydžio sandauga atstumo h nuo taško O iki jėgos veikimo linijos ... Šis produktas paimamas su pliuso ženklu, jei stiprumas linkęs pasukti kūną prieš laikrodžio rodyklę, o su ženklu – jei jėga linkęs pasukti kūną pagal laikrodžio rodyklę, tai yra ... Statmens h ilgis vadinamasjėgos petys taškas O. Jėgos veikimo poveikis t.y. tuo didesnis kūno kampinis pagreitis, tuo didesnė jėgos momento reikšmė.

1.11 pav

Su pora stiprybių vadinama sistema, susidedančia iš dviejų vienodo dydžio lygiagrečių jėgų, nukreiptų priešingomis kryptimis. Atstumas h tarp jėgų veikimo linijų vadinamaspečių pora . Poros jėgų akimirka m (F, F ") yra vienos iš jėgų, sudarančių porą ant poros peties, dydžio sandauga, paimta su atitinkamu ženklu.

Rašoma taip: m (F, F ") = ± F × h, kur sandauga imama su pliuso ženklu, jei jėgų pora linkusi sukti kūną prieš laikrodžio rodyklę ir su minuso ženklu, jei pora jėgos linkusios sukti kūną pagal laikrodžio rodyklę.

Poros jėgų momentų sumos teorema.

Poros jėgų momentų (F, F ") bet kurio taško 0 atžvilgiu suma, paimta poros veikimo plokštumoje, nepriklauso nuo šio taško pasirinkimo ir yra lygi momentui. pora.

Ekvivalentinės poros teorema. Pasekmės.

Teorema. Dvi poros, kurių momentai lygūs vienas kitam, yra lygiavertės, t.y. (F, F ") ~ (P, P")

1 išvada ... Jėgų porą galima perkelti į bet kurią jos veikimo plokštumos vietą, taip pat pasukti bet kokiu kampu ir keisti poros pečių bei jėgų dydį, išlaikant poros momentą.

2 išvada. Jėgų pora neturi rezultanto ir negali būti subalansuota viena jėga, esančia poros plokštumoje.

1.12 pav

Plokštumos porų sistemos sudėjimo ir pusiausvyros sąlyga.

1. Toje pačioje plokštumoje esančių porų sudėjimo teorema. Porų sistema, savavališkai išsidėsčiusi toje pačioje plokštumoje, gali būti pakeista viena pora, kurios momentas lygus šių porų momentų sumai.

2. Porų sistemos plokštumoje pusiausvyros teorema.

Kad absoliučiai standus kūnas būtų ramybėje, veikiamas porų sistemos, savavališkai išsidėsčiusių toje pačioje plokštumoje, būtina ir pakanka, kad visų porų momentų suma būtų lygi nuliui, t.

Svorio centras

Gravitacija - Žemės traukos jėgų, paskirstytų visame kūno tūryje, rezultatas.

Kūno svorio centras - tai toks su šiuo kūnu nuolat sujungtas taškas, per kurį bet kurioje kūno padėtyje erdvėje eina šio kūno gravitacijos jėgos veikimo linija.

Svorio centro radimo metodai

1. Simetrijos metodas:

1.1. Jei vienalytis kūnas turi simetrijos plokštumą, tada svorio centras yra šioje plokštumoje

1.2. Jei vienalytis kūnas turi simetrijos ašį, tada svorio centras yra ant šios ašies. Vienodo sukimosi kūno svorio centras yra ant sukimosi ašies.

1.3 Jei vienalytis kūnas turi dvi simetrijos ašis, tai svorio centras yra jų susikirtimo taške.

2. Skaldymo būdas: Kūnas suskaidomas į mažiausią skaičių dalių, kurių gravitacijos jėgos ir svorio centrų padėtis žinomos.

3. Neigiamų masių metodas: nustatant kūno su laisvomis ertmėmis svorio centrą reikia naudoti skaidymo būdą, tačiau laisvų ertmių masė laikytina neigiama.

Plokštumos figūros svorio centro koordinatės:

Paprastų geometrinių figūrų svorio centrų padėtis gali būti apskaičiuota naudojant žinomas formules. (1.13 pav.)

Pastaba: Figūros simetrijos svorio centras yra simetrijos ašyje.

Strypo svorio centras yra vidutinio aukščio.

1.2. Praktinių problemų sprendimo pavyzdžiai

1 pavyzdys: Krovinys pakabinamas ant strypo ir yra pusiausvyroje. Nustatykite pastangas meškerėje. (1.2.1 pav.)

Sprendimas:

Tvirtinimo strypuose atsirandančios jėgos yra lygios jėgoms, kuriomis strypai palaiko apkrovą. (5 aksioma)

Nustatome galimas jungčių „standžių strypų“ reakcijų kryptis.

Jėgos nukreipiamos išilgai strypų.

1.2.1 pav.

Atlaisvinkime tašką A nuo ryšių, jungčių veiksmą pakeisdami jų reakcijomis. (1.2.2 pav.)

Konstravimą pradedame žinoma jėga, nubrėždami vektoriųFtam tikru mastu.

Nuo vektoriaus galoFnubrėžkite linijas, lygiagrečias reakcijaiR 1 irR 2 .

1.2.2 pav

Linijų kirtimas sukuria trikampį. (1.2.3 pav.). Žinant konstrukcijų mastelį ir išmatavus trikampio kraštinių ilgį, galima nustatyti reakcijų dydžius strypuose.

Norėdami atlikti tikslesnius skaičiavimus, galite naudoti geometrinius ryšius, ypač sinusų teoremą: trikampio kraštinės ir priešingo kampo sinuso santykis yra pastovi vertė.

Šiuo atveju:

1.2.3 pav

Komentuoti: Jei vektoriaus kryptis (ryšio reakcija) pateiktoje schemoje ir jėgų trikampyje nesutampa, tada reakcija pagal schemą turėtų būti nukreipta priešinga kryptimi.

2 pavyzdys: Analitiškai nustatykite gaunamos plokščiosios konverguojančių jėgų sistemos dydį ir kryptį.

Sprendimas:

1.2.4 pav

1. Nustatykite visų sistemos jėgų projekciją į Ox (1.2.4 pav.)

Sudėjus projekcijas algebriškai, gauname rezultato projekciją į Ox ašį.

Ženklas rodo, kad rezultatas nukreiptas į kairę.

2. Nustatykite visų jėgų projekciją Oy ašyje:

Sudėjus projekcijas algebriškai, gauname rezultato projekciją į Oy ašį.

Ženklas rodo, kad rezultatas nukreiptas žemyn.

3. Nustatykite rezultato modulį pagal projekcijų reikšmes:

4. Nustatykite rezultato kampo su Ox ašimi reikšmę:

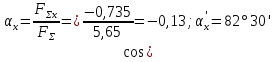
ir kampo su Oy ašimi vertė:

3 pavyzdys: Apskaičiuokite jėgų momentų sumą taško O atžvilgiu (1.2.6 pav.).

OA= AB= VD = DE = CB = 2m

1.2.6 pav

Sprendimas:

1. Jėgos momentas taško atžvilgiu yra skaitiniu požiūriu lygus jėgos modulio ir peties sandaugai.

2. Jėgos momentas lygus nuliui, jei jėgos veikimo linija eina per tašką.

4 pavyzdys: Nustatykite 1.2.7 paveiksle pavaizduoto paveikslo svorio centro padėtį

Sprendimas:

Padaliname figūrą į tris dalis:

1-stačiakampis

A 1 = 10 * 20 = 200 cm 2

2-trikampis

A 2 = 1/2 * 10 * 15 = 75 cm 2

3 apskritimas

A 3 =3,14*3 2 = 28,3 cm 2

1 paveikslo CG: x 1 = 10 cm, m 1 = 5 cm

2 paveikslo CG: x 2 = 20 + 1/3 * 15 = 25 cm, m 2 = 1/3 * 10 = 3,3 cm

3 paveikslo CG: x 3 = 10 cm, m 3 = 5 cm

Panašiai, y su = 4,5 cm

Kinematika: pagrindinės sąvokos.

Pagrindiniai kinematiniai parametrai

Trajektorija - linija, nubrėžta materialaus taško judant erdvėje. Trajektorija gali būti tiesi ir lenkta, plokščia ir erdvinė.

Plokštumos judėjimo trajektorijos lygtis: y =f ( x)

Nuvažiuotas atstumas. Kelias matuojamas išilgai tako važiavimo kryptimi. Pavadinimas -S, matavimo vienetai – metrai.

Taškinio judėjimo lygtis Tai lygtis, kuri nustato judančio taško padėtį kaip laiko funkciją.

2.1 pav

Taško padėtį kiekvienu laiko momentu galima nustatyti pagal trajektorija nuvažiuotą atstumą nuo kokio nors fiksuoto taško, laikomo pradžia (2.1 pav.). Šis judėjimo nustatymo būdas vadinamasnatūralus ... Taigi, judėjimo lygtis gali būti pavaizduota kaip S = f (t).

2.2 pav

Taip pat galima nustatyti taško padėtį, jei žinomos jo koordinatės kaip laiko funkcija (2.2 pav.). Tada, kai juda plokštuma, turi būti pateiktos dvi lygtys:

Erdvinio judėjimo atveju taip pat pridedama trečioji koordinatėz= f 3 ( t)

Šis judėjimo nurodymo būdas vadinamaskoordinuoti .

Kelionės greitis Tai vektorinis dydis, šiuo metu apibūdinantis judėjimo trajektorija greitį ir kryptį.

Greitis – vektorius bet kuriuo momentu, nukreiptas tangentiškai į trajektoriją judėjimo krypties kryptimi (2.3 pav.).

2.3 pav

Jei taškas nukeliauja vienodus atstumus per vienodą laiko tarpą, tada judėjimas vadinamasuniforma .

Vidutinis greitis kelyje ΔSyra nustatoma pagal:

kurΔS- laiku nuvažiuotas atstumas Δt; Δ t- laiko intervalas.

Jei taškas vienodais laiko intervalais nukeliauja nelygiais keliais, tada judėjimas vadinamasnetolygus ... Šiuo atveju greitis yra kintamas dydis ir priklauso nuo laikov= f( t)

Greitis šiuo metu apibrėžiamas kaip

Taško pagreitis yra vektorinis dydis, apibūdinantis greičio pokyčio dydį ir kryptį.

Taško greitis judant iš taško M1 į tašką Mg keičiasi dydžiu ir kryptimi. Vidutinis pagreitis per šį laikotarpį

Pagreitis šiuo metu:

Paprastai patogumo sumetimais laikomos dvi viena kitai statmenos pagreičio sudedamosios dalys: normalioji ir tangentinė (2.4 pav.).

Normalus pagreitis a n , apibūdina greičio kitimą kartu

kryptimi ir yra apibrėžiamas kaip

Normalus pagreitis visada yra statmenas greičiui link lanko centro.

2.4 pav

Tangentinis pagreitis a t , charakterizuoja greičio pokytį dydžiu ir visada yra nukreiptas tangentiškai į trajektoriją; greitėjant jo kryptis sutampa su greičio kryptimi, o lėtėjant – priešinga greičio vektoriaus krypčiai.

Viso pagreičio vertė apibrėžiama taip:

Judesių tipų ir kinematinių parametrų analizė

Vienodas judėjimas - šis judėjimas pastoviu greičiu:

Tiesiems, tolygiems judesiams:

Išlenktam, vienodam judėjimui:

Vienodo judėjimo dėsnis :

Lygiavertis judesys – tai judesys su pastoviu tangentiniu pagreičiu:

Tiesiai vienodam judėjimui

Kreiviniam vienodo kintamojo judesiui:

Vienodo judėjimo dėsnis:

Kinematinės grafikos

Kinematinės grafikos – tai kelio, greičio ir pagreičio pokyčių, palyginti su laiku, grafikai.

Tolygus judėjimas (2.5 pav.)

2.5 pav

Lygiavertis judesys (2.6 pav.)

2.6 pav

Paprasčiausi standaus kūno judesiai

Vertimo judesys vadinamas standaus kūno judėjimu, kai bet kuri tiesi linija ant kūno judant lieka lygiagreti pradinei jo padėčiai (2.7 pav.).

2.7 pav

Transliacinio judėjimo metu visi kūno taškai juda vienodai: greičiai ir pagreičiai kiekvieną akimirką yra vienodi.

Atsukamasis judesys visi kūno taškai apibūdina apskritimą aplink bendrą fiksuotą ašį.

Fiksuota ašis, aplink kurią sukasi visi kūno taškai, vadinamasukimosi ašis.

Tik apibūdinti kūno sukamąjį judėjimą aplink fiksuotą ašįkampiniai parametrai. (2.8 pav.)

φ - korpuso sukimosi kampas;

ω – kampinis greitis, lemia sukimosi kampo kitimą per laiko vienetą;

Kampinio greičio pokytis laikui bėgant nustatomas pagal kampinį pagreitį:

2.2. Praktinių problemų sprendimo pavyzdžiai

1 pavyzdys: Pateikta taško judėjimo lygtis. Nustatykite taško greitį trečios judėjimo sekundės pabaigoje ir vidutinį greitį per pirmąsias tris sekundes.

Sprendimas:

1. Greičio lygtis

2. Greitis trečios sekundės pabaigoje (t=3 c)

3. Vidutinis greitis

2 pavyzdys: Pagal pateiktą judėjimo dėsnį nustatykite judėjimo tipą, pradinį taško greitį ir tangentinį pagreitį, sustojimo laiką.

Sprendimas:

1. Judėjimo tipas: lygus kintamasis ()
2. Lyginant lygtis akivaizdu, kad

- pradinis takas, įveiktas prieš pradedant skaičiuoti 10m;

- pradinis greitis 20m/s

- nuolatinis tangentinis pagreitis

- pagreitis neigiamas, todėl judėjimas sulėtinamas, pagreitis nukreipiamas priešinga judėjimo greičiui.

3. Galite nustatyti laiką, kada taško greitis bus lygus nuliui.

3. Dinamika: pagrindinės sąvokos ir aksiomos

Dinamika - teorinės mechanikos skyrius, kuriame nustatomas ryšys tarp kūnų judėjimo ir juos veikiančių jėgų.

Dinamikoje išsprendžiamos dviejų tipų problemos:

nustatyti judėjimo parametrus nurodytoms jėgoms;

nustatyti kūną veikiančias jėgas, pagal pateiktus kinematinį judėjimo parametrus.

Pagalmaterialus taškas reiškia tam tikrą kūną, kuris turi tam tikrą masę (t. y. turi tam tikrą kiekį medžiagos), bet neturi linijinių matmenų (be galo mažas erdvės tūris).
Izoliuotas laikomas materialus taškas, kuriam įtakos neturi kiti materialūs taškai. Realiame pasaulyje izoliuoti materialūs taškai, kaip ir izoliuoti kūnai, neegzistuoja, ši sąvoka yra sąlyginė.

Transliacinio judėjimo metu visi kūno taškai juda vienodai, todėl kūnas gali būti laikomas materialiu tašku.

Jei kūno matmenys yra maži, palyginti su trajektorija, jis taip pat gali būti laikomas materialiu tašku, o taškas sutampa su kūno svorio centru.

Sukamojo kūno judėjimo metu taškai gali judėti nevienodai, tokiu atveju kai kurios dinamikos nuostatos gali būti taikomos tik atskiriems taškams, o materialus objektas gali būti laikomas materialių taškų visuma.

Todėl dinamika skirstoma į taško dinamiką ir materialinės sistemos dinamiką.

Dinamikos aksiomos

Pirmoji aksioma ( inercijos principas): in Bet kuris izoliuotas materialus taškas yra ramybės būsenoje arba tolygiai ir tiesiai juda tol, kol veikiamos jėgos išveda jį iš šios būsenos.

Ši būsena vadinama valstybeinercija. Pašalinti tašką iš šios būsenos, t.y. suteikti jai šiek tiek pagreitį, išorinė jėga gali.

Kiekvienas kūnas (taškas) turiinercija. Kūno masė yra inercijos matas.

Pagal masę yra vadinamimedžiagos kiekis kūno tūryje, klasikinėje mechanikoje ji laikoma pastovia verte. Masės matavimo vienetas yra kilogramas (kg).

Antroji aksioma (Antrasis Niutono dėsnis yra pagrindinis dinamikos dėsnis)

F = ma

kurT - taškinė masė, kg;a - taško pagreitis, m / s 2 .

Medžiagajam taškui jėga suteikiamas pagreitis yra proporcingas jėgos dydžiui ir sutampa su jėgos kryptimi.

Gravitacija veikia visus Žemės kūnus, ji suteikia kūnui gravitacijos pagreitį, nukreiptą į Žemės centrą:

G = mg,

kurg - 9,81 m / s², gravitacijos pagreitis.

Trečioji aksioma (Trečiasis Niutono dėsnis): cdviejų kūnų sąveikos dumblai yra vienodo dydžio ir nukreipti išilgai vienos tiesės skirtingomis kryptimis.

Sąveikaujant pagreičiai yra atvirkščiai proporcingi masėms.

Ketvirta aksioma (jėgų veikimo nepriklausomybės dėsnis): įKiekviena jėgų sistemos jėga veikia taip, kaip veiktų viena.

Pagreitis, kurį tašką suteikia jėgų sistema, yra lygus pagreičių, kuriuos tašką suteikia kiekviena jėga atskirai, geometrinei sumai (3.1 pav.):

3.1 pav

Trinties koncepcija. Trinties rūšys.

Trintis- pasipriešinimas, atsirandantis dėl vieno šiurkštaus kūno judėjimo kito paviršiumi. Kūnams slystant atsiranda slydimo trintis, riedant – siūbavimo trintis.

Slydimo trintis

3.2 pav.

Priežastis yra mechaninis iškyšų sujungimas. Atsparumo judėjimui jėga slystant vadinama slydimo trinties jėga (3.2 pav.)

Slydimo trinties dėsniai:

1. Slydimo trinties jėga yra tiesiogiai proporcinga normaliam slėgio jėgai:

kurR- normalaus slėgio jėga, nukreipta statmenai atraminiam paviršiui;f- slydimo trinties koeficientas.

3.3 pav.

Kai kūnas juda pasvirusioje plokštumoje (3.3 pav.)

Riedėjimo trintis

Pasipriešinimas riedėjimui yra susijęs su abipuse grunto ir rato deformacija ir yra žymiai mažesnė slydimo trintis.

Kad ratas riedėtų tolygiai, reikia naudoti jėgąF dv (3.4 pav.)

Rato riedėjimo sąlyga yra tokia, kad judėjimo momentas turi būti ne mažesnis už pasipriešinimo momentą:

3.4 pav.

1 pavyzdys: 2 pavyzdys: Į du materialius taškus su masem 1 = 2 kg irm 2 = 5 kg, taikomos tos pačios jėgos. Greičiau palyginkite vertes.

Sprendimas:

Pagal trečiąją aksiomą pagreičio dinamika yra atvirkščiai proporcinga masėms:

3 pavyzdys: Nustatykite gravitacijos darbą, kai krovinys perkeliamas iš taško A į tašką C išilgai nuožulnios plokštumos (3. 7 pav.). Kūno gravitacijos jėga yra 1500 N. AB = 6 m, BC = 4 m. 3 pavyzdys: Nustatykite pjovimo jėgos darbą per 3 min. Ruošinio sukimosi greitis 120 aps./min, ruošinio skersmuo 40mm, pjovimo jėga 1kN. (3.8 pav.)

Sprendimas:

1. Darbas sukamaisiais judesiais:

2. Kampinis greitis 120 aps./min

3.8 pav.

3. Apsisukimų skaičius tam tikram laikui yraz= 120 * 3 = 360 aps.

Sukimosi kampas per šį laiką yra φ = 2πz= 2 * 3,14 * 360 = 2261rad

4. Dirbkite 3 posūkiais:W= 1 * 0,02 * 2261 = 45,2 kJ

Bibliografija

Olofinskaja, V.P. „Techninė mechanika“, Maskvos „Forumas“ 2011 m

Erdedi A.A. Erdedi N.A. Teorinė mechanika. Medžiagų atsparumas.- Rn-D; Feniksas, 2010 m

Pasidalinkite straipsniu su draugais:

Panašūs straipsniai

• 

  Kodėl dieną nematai žvaigždžių?
• 

  Įmonės rinkodaros vertinimo kriterijai
• 

  Marketingo veiklos efektyvumo kriterijai