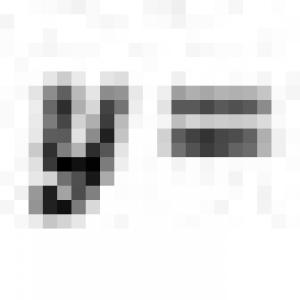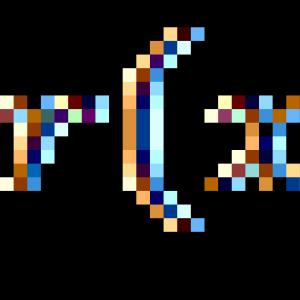Enačba oblike tgx. Ločna tangenta in kotangens loka

Valovna enačba, delna diferencialna enačba, ki opisuje postopek širjenja motenj v določenem okolju A. N. Tikhonov in A. A. Samarskii, Enačbe matematične fizike, 3. izd., Moskva, 1977. - str. 155 ....

Klasifikacije hiperboličnih parcialnih diferencialnih enačb

Enačba prevodnosti toplote je delna diferencialna enačba paraboličnega tipa, ki opisuje postopek širjenja toplote v neprekinjenem mediju (plin ...

Matematične metode, uporabljene v teoriji čakalnih sistemov

Verjetnosti stanj sistema lahko najdemo iz sistema diferencialnih enačb Kolmogorov, ki so sestavljeni po naslednjem pravilu: Na levi strani vsake od njih je izpeljava verjetnosti i-tega stanja ...

Nestacionarna Riccatijeva enačba

(1) Splošna Riccatijeva enačba ima obliko :, (1.1) kjer so P, Q, R neprekinjene funkcije x, kadar x spremembe v intervalu Enačba (1.1) vsebuje enačbe, ki smo jih že obravnavali kot posebne primere: ker dobimo linearno enačbo, za - enačbo Bernoulli ...

Osnove znanstvenega raziskovanja in načrtovanja prometnih poskusov

Funkcionalno odvisnost Y \u003d f (X) (regresijska enačba) dobimo z metodo najmanjših kvadratov (OLS). Kot približne funkcije uporabite linearne (Y \u003d a0 + a1X) in kvadratne odvisnosti (Y \u003d a0 + a1X + a2X2). Z uporabo metode najmanjših kvadratov vrednosti a0 ...

Pol polarnega koordinatnega sistema postavimo na izhodišče pravokotnega koordinatnega sistema, polarna os je združljiva s pozitivno polovično os os (slika 3). Slika: 3 Vzemimo enačbo ravne črte v normalni obliki: (3.1) - dolžina pravokotnika ...

Polarni koordinatni sistem na ravnini

Zapišimo enačbo v polarnih koordinatah kroga, ki gre skozi pol, centrirano na polarno os in polmer R. Iz pravokotnega trikotnika OAA dobimo OA \u003d OA (slika 4) ...

Koncepti selektivne teorije. Distribucijske serije. Korelacijska in regresijska analiza

Študija: a) koncept parne linearne regresije; b) priprava sistema normalnih enačb; c) lastnosti ocen po metodi najmanjših kvadratov; d) metoda za iskanje enačbe linearne regresije. Recimo ...

Konstrukcija rešitev diferencialnih enačb v obliki potencialnih vrst

Kot primer uporabe zgrajene teorije razmislimo o Besselovi enačbi: (6.1) Kje. Edinstvena točka z \u003d 0 je pravilna. V zadnjem delu letala ni drugih lastnosti. V enačbi (6.1) ima torej vladajoča enačba obliko, to je ...

Reševanje matričnih enačb

Tudi matrično enačbo ХА \u003d В lahko rešimo na dva načina: 1. Inverzno matriko izračunamo s katero koli od znanih metod. Potem bo rešitev matrične enačbe imela obliko: 2 ...

Reševanje matričnih enačb

Zgoraj opisane metode niso primerne za reševanje enačb oblike AX \u003d XB, AX + XB \u003d C. Prav tako niso primerni za reševanje enačb, v katerih je vsaj eden od dejavnikov za neznano matrico X izrojena matrica ...

Reševanje matričnih enačb

Enačbe oblike AX \u003d XA se rešujejo na enak način kot v prejšnjem primeru, torej element za elementom. Rešitev se tukaj nanaša na iskanje permutacijske matrike. Oglejmo si podrobneje primer. Primer. Poišči vse matrike ...

Stacionarno delovanje omrežja v čakalni vrsti z diamantno konturo

Iz stanja lahko preide v eno od naslednjih stanj: - zaradi prejema zahteve v čakalno vrsto prvega vozlišča z intenzivnostjo; - zaradi prejema iz prvega vozlišča obdelane zahteve v njem v vrsto tretjega vozlišča z intenzivnostjo pri ...

Trigonometrične funkcije

Arktangens števila je število, katerega sinus je enak: če in. Vse korenine enačbe lahko najdemo po formuli: ...

Numerične metode za reševanje matematičnih problemov

\u003e\u003e Ločna tangenta in kotangens loka. Rešitev enačb tgx \u003d a, ctgx \u003d a

§ 19. Ločna tangenta in obločni kotangens. Rešitev enačb tgx \u003d a, ctgx \u003d a

V primeru 2 §16 nismo mogli rešiti treh enačb:

Dva smo že rešili - prvega v § 17 in drugega v § 18, zato smo morali uvesti koncepte arkokozin in arcsine. Razmislite o tretji enačbi x \u003d 2.
Grafi funkcij y \u003d tg x in y \u003d 2 imajo neskončno veliko skupnih točk, abscide vseh teh točk so v obliki - abscisa presečišča ravne črte y \u003d 2 z glavno vejo tangentoida (slika 90). Za število x1 so matematiki pripravili zapis arctg 2 (beri "arctangent of two"). Potem lahko vse korenine enačbe x \u003d 2 opišemo s formulo x \u003d arctg 2 + nk.
Kaj je arctg 2? To je številka tangenta ki je enako 2 in ki spada v interval
Poglejmo zdaj enačbo tg x \u003d -2.
Grafi funkcij imajo neskončno veliko skupnih točk, abscide vseh teh točk imajo obliko abscisa presečišča ravne črte y \u003d -2 z glavno vejo tangentoida. Za število x 2 so matematiki pripravili zapis arctg (-2). Potem lahko vse korenine enačbe x \u003d -2 opišemo s formulo

Kaj je arctg (-2)? To je število, katerega tangenta je -2 in spada v interval. Bodite pozorni (glejte sliko 90): x 2 \u003d -x 2. To pomeni, da je arctg (-2) \u003d - arctg 2.
Oblikujmo splošno definicijo arktangensa.

Opredelitev 1. arctg a (arktangens a) je število iz intervala, katerega tangenta je enaka a. Torej,

Zdaj lahko sprejmemo splošen zaključek o rešitvi enačbe x \u003d a: enačba x \u003d a ima rešitve

Zgoraj smo ugotovili, da je arctg (-2) \u003d -agstg 2. Na splošno je za katero koli vrednost a formula

Primer 1. Izračunaj:

2. primer Reši enačbe:

A) Sestavimo formulo rešitve:

Vrednosti arktangente v tem primeru ne moremo izračunati, zato bomo rešitev enačbe pustili v dobljeni obliki.
Odgovor:
3. primer Reši neenakosti:
Neenakost v pogledu lahko rešimo grafično z upoštevanjem naslednjih načrtov
1) konstruiramo tangentoid y \u003d tan x in premico y \u003d a;
2) za glavno vejo tangizoide dodeli interval osi x, na katerem je izpolnjena določena neenakost;
3) ob upoštevanju pogostosti funkcije y \u003d tg x odgovor zapišite v splošni obliki.
Ta načrt uporabimo za reševanje danih neenakosti.

: a) Sestavimo grafe funkcij y \u003d tanx in y \u003d 1. Na glavni veji tangentoida se sekata v točki

Izberite interval osi x, na katerem je glavna veja tangentoida pod ravno črto y \u003d 1, to je interval
Ob upoštevanju periodičnosti funkcije y \u003d tgx ugotavljamo, da je navedena neenakost izpolnjena na katerem koli intervalu obrazca:

Združitev vseh takih intervalov je splošna rešitev dane neenakosti.
Odgovor lahko zapišemo na drug način:

b) Sestavimo grafe funkcij y \u003d tg x in y \u003d -2. Na glavni veji tangentoida (slika 92) se sekata v točki x \u003d arctg (-2).

Izberite interval osi x, na kateri je glavna veja tangentoida

Razmislite o enačbi s tan x \u003d a, kjer je a\u003e 0. Grafa funkcij y \u003d ctg x in y \u003d a imata neskončno veliko skupnih točk, abscisi vseh teh točk so v obliki: x \u003d x 1 + nk, kjer je x 1 \u003d arcctg a abscisa točke presečišča ravne črte y \u003d a z glavno vejo tangentoida (sl. 93). Arcctg a je torej število, katerega kotangens je enak a in ki pripada intervalu (0, n); na tem intervalu je zgrajena glavna veja grafa funkcije y \u003d ctg x.

Na sl. 93 prikazuje tudi grafično ponazoritev rešitve enačbe c1tg \u003d -a. Grafa funkcij y \u003d ctg x in y \u003d -a imata neskončno veliko skupnih točk, abscise vseh teh točk imajo obliko x \u003d x 2 + nk, kjer je x 2 \u003d arcctg (- a) abscisa presečišča premice y \u003d -a z glavnim tangentoidna veja. Arcctg (-a) je torej število, katerega kotangens je -a in spada v interval (O, n); na tem intervalu je zgrajena glavna veja grafa funkcije Y \u003d ctg x.

Opredelitev 2.arcctg a (arc kotangens a) je število iz intervala (0, n), katerega kotangens je a.
Torej,

Zdaj lahko naredimo splošen zaključek o rešitvi enačbe ctg x \u003d a: enačba ctg x \u003d a ima rešitve:

Bodite pozorni (glejte sliko 93): x 2 \u003d n-x 1. To pomeni

4. primer Izračunaj:

A) smo postavili

Enačbo ctg x \u003d a lahko skoraj vedno pretvorimo v obliko Izjema je enačba ctg x \u003d 0. Toda v tem primeru izkoristite dejstvo, do katerega lahko greste
enačba cos x \u003d 0. Tako enačba oblike x \u003d a ni neodvisna.

A.G. Mordkovičeva algebra 10. razred

Koledarsko-tematsko načrtovanje v matematiki, video iz matematike na spletu, matematika v šoli prenesi

Vsebina lekcije oris lekcije podpora okvirna predstavitev lekcije pospeševalne metode interaktivne tehnologije Vadite naloge in vaje delavnice samotestiranja, treningi, primeri, naloge domače naloge razprava vprašanja retorična vprašanja študentov Ilustracije avdio, video posnetke in večpredstavnost fotografije, grafikoni, tabele, sheme humor, šale, zabava, stripovske prilike, reki, križanke, citati Dodatki povzetki članki čipi za radovedne varalnice učbeniki osnovno in dodatno besedišče izrazov drugo Izboljšanje učbenikov in lekcij popravki napak v vadnici posodabljanje drobca v učbeniških elementih inovativnosti na lekciji, ki nadomešča zastarela znanja z novimi Samo za učitelje popolne lekcije koledarski načrt za leto metodološka priporočila razpravnega programa Integrirane lekcije

Prej v programu so študentje dobili idejo o reševanju trigonometričnih enačb, se seznanili s konceptoma inverznega kosinusa in arksinusa, primeri rešitev enačb cos t \u003d a in sin t \u003d a. V tej video vadnici razmislite o reševanju enačb tg x \u003d a in ctg x \u003d a.

Na začetku študije te teme upoštevajte enačbi tg x \u003d 3 in tg x \u003d - 3. Če enačbo tg x \u003d 3 rešite z grafom, bomo videli, da ima presečišče grafov funkcij y \u003d tg x in y \u003d 3 neskončen nabor rešitev, kjer je x \u003d x 1 + πk. Vrednost x 1 je koordinata x presečišča grafov funkcij y \u003d tg x in y \u003d 3. Avtor uvaja pojem arktangens: arctg 3 je število, katerega tg je 3, in to število pripada intervalu od -π / 2 do π / 2. Rešitev enačbe tg x \u003d 3 lahko s pomočjo koncepta arktangente zapišemo kot x \u003d arctan 3 + πk.

Po analogiji je rešena enačba tg x \u003d - 3. Glede na zgrajene grafe funkcij y \u003d tg x in y \u003d - 3 je razvidno, da bodo presečišča grafov in s tem tudi rešitve enačb x \u003d x 2 + πk. Rešitev lahko z arktangensom zapišemo kot x \u003d arctan (- 3) + πk. Na naslednji sliki lahko vidimo, da je arctan (- 3) \u003d - arctan 3.

Splošna opredelitev arktangente je naslednja: arktangens a je število iz intervala od -π / 2 do π / 2, katerega tangenta je enaka a. Potem je rešitev enačbe tg x \u003d a x \u003d arctan a + πk.

Avtor poda primer 1. Poiščite rešitev izraza arctg. Uvedimo zapis: arktangens števila je enak x, potem bo tan x enak temu številu, kjer x pripada odseku od -π / 2 do π / 2. Kot v primerih v prejšnjih temah bomo uporabili tabelo vrednosti. Po tej tabeli tangenta tega števila ustreza vrednosti x \u003d π / 3. Zapišimo rešitev enačbe, arktangens določenega števila je enak π / 3, tudi π / 3 pripada intervalu od -π / 2 do π / 2.

Primer 2 - Izračunajte arktangens negativnega števila. Z enačbo arctan (- a) \u003d - arctan a vnesite vrednost x. Podobno kot v primeru 2 zapišemo vrednost x, ki pripada segmentu od -π / 2 do π / 2. Iz tabele vrednosti ugotovimo, da je x \u003d π / 3, torej - tg x \u003d - π / 3. Odgovor na enačbo je - π / 3.

Razmislite o primeru 3. Rešite enačbo tan x \u003d 1. Zapišemo, da je x \u003d arctan 1 + πk. V tabeli vrednost tg 1 ustreza vrednosti x \u003d π / 4, zato je arctan 1 \u003d π / 4. To vrednost nadomestite v prvotno formulo x in zapišite odgovor x \u003d π / 4 + πk.

Primer 4: izračunajte tg x \u003d - 4.1. V tem primeru je x \u003d arctan (- 4,1) + πk. Ker vrednosti arktana v tem primeru ni mogoče najti, odgovor bo videti tako: x \u003d arctan (- 4,1) + πk.

V primeru 5 je obravnavana rešitev neenakosti tg x\u003e 1. Za njeno rešitev zgradimo grafe funkcij y \u003d tg x in y \u003d 1. Kot lahko vidite na sliki, se ti grafi sekajo v točkah x \u003d π / 4 + πk. Ker v tem primeru tg x\u003e 1, na grafu izberemo površino tangentoida, ki se nahaja nad grafom y \u003d 1, kjer x pripada intervalu od π / 4 do π / 2. Odgovor zapišemo kot π / 4 + πk< x < π/2 + πk.

Nato upoštevajte enačbo ctg x \u003d a. Na sliki so prikazani grafi funkcij y \u003d ctg x, y \u003d a, y \u003d - a, ki imajo veliko presečišč. Rešitve lahko zapišemo kot x \u003d x 1 + πk, kjer je x 1 \u003d arcctg a in x \u003d x 2 + πk, kjer je x 2 \u003d arcctg (- a). Opozoriti je treba, da je x 2 \u003d π - x 1. To pomeni enakost arcctg (- a) \u003d π - arcctg a. Nadalje je podana definicija obločnega kotangente: obločni kotangens a je število iz intervala od 0 do π, katerega kotangens je enak a. Rešitev enačbe ctg x \u003d a je zapisana kot: x \u003d arcctg a + πk.

Na koncu video lekcije je še en pomemben zaključek - izraz ctg x \u003d a lahko zapišemo v obliki tg x \u003d 1 / a, če a ni enak nič.

KODA BESEDILA:

Razmislimo o rešitvi enačb tan x \u003d 3 in tan x \u003d - 3. Pri grafični rešitvi prve enačbe vidimo, da imajo grafi funkcij y \u003d tan x in y \u003d 3 neskončno veliko presečišč, katerih abscise zapišemo v obliki

x \u003d x 1 + πk, kjer je x 1 abscisa presečišča ravne črte y \u003d 3 z glavno vejo tangentoida (slika 1), za katero je bil skovan zapis

arctan 3 (arktangens tri).

Kako razumete arctg 3?

To je število, katerega tangenta je 3 in to število pripada intervalu (-;). Potem lahko vse korenine enačbe tan x \u003d 3 zapišemo s formulo x \u003d arctan 3 + πk.

Podobno lahko rešitev enačbe tan х \u003d - 3 zapišemo v obliki х \u003d х 2 + πk, kjer je х 2 abscisa presečišča ravne črte у \u003d - 3 z glavno vejo tangentoida (slika 1), za katero je zapis arktan (- 3) (arktangens minus tri). Potem lahko vse korenine enačbe zapišemo s formulo: x \u003d arctan (-3) + πk. Slika prikazuje, da je arctan (- 3) \u003d - arctan 3.

Oblikujmo definicijo arktangensa. Arktangens a je število iz intervala (-;), katerega tangenta je enaka a.

Pogosto se uporablja enakost: arctan (-a) \u003d -arctan a, kar velja za vse a.

Ker poznamo definicijo arktangense, naredimo splošen zaključek o reševanju enačbe

tg x \u003d a: enačba tg x \u003d a ima rešitev x \u003d arctan a + πk.

Oglejmo si nekaj primerov.

PRIMER 1: Izračunaj arctg.

Sklep. Naj bo arctan \u003d x, nato tgx \u003d in xϵ (-;). Pokaži tabelo vrednosti Zato je x \u003d, saj je tg \u003d in ϵ (-;).

Torej arctg \u003d.

PRIMER 2. Izračunajte arktan (-).

Sklep. Z uporabo enakosti arctan (- a) \u003d - arctan a zapišemo:

arctg (-) \u003d - arctg. Naj - arctan \u003d x, nato - tgx \u003d in xϵ (-;). Zato je x \u003d, saj je tg \u003d in ϵ (-;). Prikaži tabelo vrednosti

Zato - arctan \u003d - tgх \u003d -.

PRIMER 3. Reši enačbo tgx \u003d 1.

1. Zapišimo formulo za rešitve: х \u003d arctan 1 + πk.

2. Poiščite vrednost arktangenta

saj je tg \u003d. Prikaži tabelo vrednosti

Zato je arctg1 \u003d.

3. Najdite vrednost v formuli za rešitve:

PRIMER 4. Rešimo enačbo tgx \u003d - 4,1 (tangenta x je enaka minus štiri celi desetinki).

Sklep. Zapišimo formulo za rešitve: x \u003d arctan (- 4,1) + πk.

Vrednosti arktangenca ne moremo izračunati, zato bomo rešitev enačbe pustili v dobljeni obliki.

PRIMER 5. Reši neenakost tgх 1.

Sklep. Rešili bomo grafično.

1. Sestavimo tangentoid

y \u003d tanx in ravna črta y \u003d 1 (slika 2). Sekajo se na točkah oblike х \u003d + πk.

2. Izberite interval osi x, na katerem je glavna veja tangentoida nad premico y \u003d 1, saj je po pogoju tgx 1. To interval (;).

3. Uporabljamo periodičnost funkcije.

Lastnost 2. у \u003d tg х - periodična funkcija z glavnim obdobjem π.

Ob upoštevanju periodičnosti funkcije y \u003d tgx zapišemo odgovor:

(;). Odgovor lahko zapišemo kot dvojno neenakost:

Preidemo na enačbo ctg x \u003d a. Predstavimo grafično ponazoritev rešitve enačbe za pozitivno in negativno a (slika 3).

Grafi funkcij y \u003d ctg x in y \u003d a in

y \u003d ctg x in y \u003d -a

imajo neskončno veliko skupnih točk, katerih abscide so:

x \u003d x 1 +, kjer je x 1 abscisa presečišča ravne črte y \u003d a z glavno vejo tangentoida in

x 1 \u003d arcсtg a;

x \u003d x 2 +, kjer je x 2 abscisa presečišča črte

y \u003d - a z glavno vejo tangentoida in x 2 \u003d arcсtg (- a).

Upoštevajte, da je x 2 \u003d π - x 1. Zapišimo torej pomembno enakost:

arcсtg (-а) \u003d π - arcсtg а.

Oblikujmo definicijo: obločni kotangens a je število iz intervala (0; π), katerega kotangens je enak a.

Rešitev enačbe ctg x \u003d a je zapisana v obliki: x \u003d arcctg a +.

Upoštevajte, da lahko enačbo ctg x \u003d a pretvorimo v obliko

tg x \u003d, razen kadar je a \u003d 0.

V tej lekciji bomo nadaljevali s preučevanjem arktangense in reševanjem enačb oblike tg x \u003d a za kateri koli a. Na začetku lekcije bomo enačbo rešili z vrednostjo tabele in rešitev ponazorili na grafu, nato pa na krogu. Nato rešimo enačbo tgx \u003d a v splošni obliki in izpeljemo splošno formulo za odgovor. Izračune bomo ponazorili na grafu in krogu ter upoštevali različne oblike odgovora. Na koncu pouka bomo rešili več nalog z ilustracijo rešitev na grafu in na krožnici.

Tema: Trigonometrične enačbe

Lekcija: Ločna tangenta in reševanje enačbe tgx \u003d a (nadaljevanje)

1. Tema lekcije, uvod

V tej lekciji bomo preučili reševanje enačbe za katero koli realno

2. Rešitev enačbe tgx \u003d √3

Naloga 1. Reši enačbo

Poiščimo rešitev z uporabo grafov funkcij (slika 1).

Upoštevajte interval Na tem intervalu je funkcija monotona, kar pomeni, da je dosežena samo za eno vrednost funkcije.

Odgovor:

Rešimo isto enačbo s številskim krogom (slika 2).

Odgovor:

3. Rešitev enačbe tgx \u003d a v splošni obliki

Rešimo enačbo v splošni obliki (slika 3).

Na intervalu ima enačba edinstveno rešitev

Najmanjše pozitivno obdobje

Ponazorimo na številčnem krogu (slika 4).

4. Reševanje problemov

Naloga 2. Reši enačbo

Spremenite spremenljivko

Naloga 3. Rešite sistem:

Rešitev (slika 5):

V točki je vrednost torej rešitev sistema le točka

Odgovor:

Naloga 4. Reši enačbo

Rešimo s spreminjanjem spremenljivke:

Problem 5. Poiščite število rešitev enačbe na intervalu

Rešimo problem z uporabo grafa (slika 6).

Enačba ima tri rešitve v danem intervalu.

Ponazorimo na številčnem krogu (slika 7), čeprav to ni tako jasno kot na grafu.

Odgovor: Tri rešitve.

5. Zaključek, zaključek

Enačbo za katero koli realno smo rešili z uporabo pojma arktangens. V naslednji lekciji se bomo seznanili s konceptom loka kotangens.

Bibliografija

1. Algebra in začetek analize, ocena 10 (v dveh delih). Učbenik za izobraževalne ustanove (profilna raven), ur. A.G.Mordkovich. -M.: Mnemosina, 2009.

2. Algebra in začetek analize, ocena 10 (v dveh delih). Problematika za izobraževalne ustanove (nivo profila), ur. A.G.Mordkovich. -M.: Mnemosina, 2007.

3. Vilenkin N. Ya., Ivashev-Musatov OS, Schwarzburd SI Algebra in matematična analiza za 10. razred (učbenik za učence v šolah in razredih z naprednim študijem matematike). - M.: Education, 1996.

4. Galitsky M. L., Moshkovich M. M., Shvartsburd S. I. Poglobljeni študij algebre in matematične analize.-M.: Education, 1997.

5. Zbirka matematičnih problemov za prosilce na visokošolske ustanove (pod uredništvom MI Skanavi). - M .: Višja šola, 1992.

6. Merzlyak A. G., Polonsky V. B., Yakir M. S. Algebrski simulator.-K.: A. S.K., 1997.

7. Sahakyan S. M., Goldman A. M., Denisov D. V. Problemi v algebri in principi analize (priročnik za učence od 10. do 11. razreda splošnih izobraževalnih ustanov). - M.: Izobraževanje, 2003.

8. Karp AP Zbirka problemov iz algebre in principi analize: učbenik. dodatek za 10-11 razrede s poglabljanjem študij matematika.-M.: Izobraževanje, 2006.

Domača naloga

Algebra in začetek analize, ocena 10 (v dveh delih). Problematika za izobraževalne ustanove (nivo profila), ur. A.G.Mordkovich. -M.: Mnemosina, 2007.

№№ 22.18, 22.21.

Dodatni spletni viri

1. Matematika.

2. Težave z internetnim portalom. ru.

3. Izobraževalni portal za pripravo na izpite.

Lahko naročite podrobno rešitev problema !!!

Enakost, ki vsebuje neznanko pod znakom trigonometrične funkcije (`sin x, cos x, tan x` ali` ctg x`), se imenuje trigonometrična enačba in njihove formule bomo nadalje preučili.

Najenostavnejše enačbe se imenujejo "sin x \u003d a, cos x \u003d a, tg x \u003d a, ctg x \u003d a`, kjer je" x "- kot, ki ga najdemo," a "- poljubno število. Zapišite si korenske formule za vsako od njih.

1. Enačba "sin x \u003d a".

Kajti `| a |\u003e 1` nima rešitev.

Za `| a | \\ leq 1` ima neskončno število rešitev.

Koreninska formula: `x \u003d (- 1) ^ n arcsin a + \\ pi n, n \\ in Z`

2. Enačba "cos x \u003d a"

Za `| a |\u003e 1` - tako kot v primeru sinusa nima rešitev med realnimi števili.

Za `| a | \\ leq 1` ima neskončno število rešitev.

Korenska formula: `x \u003d \\ pm arccos a + 2 \\ pi n, n \\ in Z`

Posebni primeri sinusov in kosinusov v grafih.

3. Enačba "tg x \u003d a"

Ima neskončno število rešitev za poljubne vrednosti "a".

Koren formula: `x \u003d arctan a + \\ pi n, n \\ in Z`

4. Enačba "ctg x \u003d a"

Prav tako ima neskončno število rešitev za poljubne vrednosti "a".

Koren formula: `x \u003d arcctg a + \\ pi n, n \\ in Z`

Formule za korenine trigonometričnih enačb v tabeli

Za sinus:
Za kosinus:
Za tangento in kotangens:
Formule za reševanje enačb, ki vsebujejo inverzne trigonometrične funkcije:

Metode reševanja trigonometričnih enačb

Rešitev katere koli trigonometrične enačbe je sestavljena iz dveh stopenj:

• z uporabo pretvori v najpreprostejše;
• rešite nastalo najpreprostejšo enačbo z uporabo zgornjih zapisanih korenskih formul in tabel.

Oglejmo si primere glavnih načinov reševanja.

Algebrajska metoda.

Pri tej metodi se izvede nadomestitev spremenljivk in zamenjava v enakost.

Primer. Rešite enačbo: `2cos ^ 2 (x + \\ frac \\ pi 6) -3sin (\\ frac \\ pi 3 - x) + 1 \u003d 0`

`2cos ^ 2 (x + \\ frac \\ pi 6) -3cos (x + \\ frac \\ pi 6) + 1 \u003d 0`,

spremenimo: `cos (x + \\ frac \\ pi 6) \u003d y`, nato` 2y ^ 2-3y + 1 \u003d 0`,

najdemo korenine: `y_1 \u003d 1, y_2 \u003d 1 / 2`, od koder sledita dva primera:

1. `cos (x + \\ frac \\ pi 6) \u003d 1`,` x + \\ frac \\ pi 6 \u003d 2 \\ pi n`, `x_1 \u003d - \\ frac \\ pi 6 + 2 \\ pi n`.

2. `cos (x + \\ frac \\ pi 6) \u003d 1 / 2`,` x + \\ frac \\ pi 6 \u003d \\ pm arccos 1/2 + 2 \\ pi n`, `x_2 \u003d \\ pm \\ frac \\ pi 3- \\ frac \\ pi 6 + 2 \\ pi n`.

Odgovor: `x_1 \u003d - \\ frac \\ pi 6 + 2 \\ pi n`,` x_2 \u003d \\ pm \\ frac \\ pi 3- \\ frac \\ pi 6 + 2 \\ pi n`.

Faktorizacija.

Primer. Reši enačbo: `sin x + cos x \u003d 1`.

Sklep. Premakni vse izraze enakosti v levo: "sin x + cos x-1 \u003d 0". Uporaba, pretvorba in faktor leve strani:

`sin x - 2sin ^ 2 x / 2 \u003d 0`,

`2sin x / 2 cos x / 2-2sin ^ 2 x / 2 \u003d 0`,

"2sin x / 2 (cos x / 2-sin x / 2) \u003d 0",

1. `sin x / 2 \u003d 0`,` x / 2 \u003d \\ pi n`, `x_1 \u003d 2 \\ pi n`.
2. `cos x / 2-sin x / 2 \u003d 0`,` tg x / 2 \u003d 1`, `x / 2 \u003d arctan 1+ \\ pi n`,` x / 2 \u003d \\ pi / 4 + \\ pi n` , `x_2 \u003d \\ pi / 2 + 2 \\ pi n`.

Odgovor: `x_1 \u003d 2 \\ pi n`,` x_2 \u003d \\ pi / 2 + 2 \\ pi n`.

Redukcija na homogeno enačbo

Najprej morate to trigonometrično enačbo pripeljati do ene od dveh vrst:

`Sin x + b cos x \u003d 0` (homogena enačba prve stopnje) ali` sin sin ^ 2 x + b sin x cos x + c cos ^ 2 x \u003d 0` (homogena enačba druge stopnje).

Nato oba dela razdelite z "cos x \\ ne 0" - za prvi primer in z "cos ^ 2 x \\ ne 0" - za drugi primer. Za "tg x" dobimo enačbi: "a tg x + b \u003d 0" in "a tg ^ 2 x + b tg x + c \u003d 0", ki ju je treba rešiti z znanimi metodami.

Primer. Reši enačbo: "2 sin ^ 2 x + sin x cos x - cos ^ 2 x \u003d 1".

Sklep. Desno stran napišite kot "1 \u003d sin ^ 2 x + cos ^ 2 x":

`2 sin ^ 2 x + sin x cos x - cos ^ 2 x \u003d" sin ^ 2 x + cos ^ 2 x ",

`2 sin ^ 2 x + sin x cos x - cos ^ 2 x-" sin ^ 2 x - cos ^ 2 x \u003d 0 "

`sin ^ 2 x + sin x cos x - 2 cos ^ 2 x \u003d 0`.

To je homogena trigonometrična enačba druge stopnje, njeno levo in desno stran delimo z "cos ^ 2 x \\ ne 0", dobimo:

`\\ frac (sin ^ 2 x) (cos ^ 2 x) + \\ frac (sin x cos x) (cos ^ 2 x) - \\ frac (2 cos ^ 2 x) (cos ^ 2 x) \u003d 0"

`tg ^ 2 x + tg x - 2 \u003d 0`. Uvedemo nadomestni `tg x \u003d t`, posledično` t ^ 2 + t - 2 \u003d 0`. Koreni te enačbe so "t_1 \u003d -2" in "t_2 \u003d 1". Nato:

1. `tg x \u003d -2`,` x_1 \u003d arctg (-2) + \\ pi n`, `n \\ v Z`
2. `tg x \u003d 1`,` x \u003d arctan 1+ \\ pi n`, `x_2 \u003d \\ pi / 4 + \\ pi n`,` n \\ v Z`.

Odgovor. `x_1 \u003d arctg (-2) + \\ pi n`,` n \\ in Z`, `x_2 \u003d \\ pi / 4 + \\ pi n`,` n \\ in Z`.

Pojdi na pol vogala

Primer. Reši enačbo: `11 sin x - 2 cos x \u003d 10`.

Sklep. Kot rezultat uporabite formule dvojnega kota: "22 sin (x / 2) cos (x / 2)-" 2 cos ^ 2 x / 2 + 2 sin ^ 2 x / 2 \u003d "10 sin ^ 2 x / 2 +10 cos ^ 2 x / 2`

`4 tg ^ 2 x / 2 - 11 tg x / 2 + 6 \u003d 0"

Z uporabo zgornje algebarske metode dobimo:

1. `tg x / 2 \u003d 2`,` x_1 \u003d 2 arctan 2 + 2 \\ pi n`, `n \\ in Z`,
2. `tg x / 2 \u003d 3/4`,` x_2 \u003d arctan 3/4 + 2 \\ pi n`, `n \\ v Z`.

Odgovor. `x_1 \u003d 2 arctan 2 + 2 \\ pi n, n \\ in Z`,` x_2 \u003d arctan 3/4 + 2 \\ pi n`, `n \\ v Z`.

Predstavljamo pomožni kot

V trigonometrični enačbi "sin x + b cos x \u003d c", kjer so a, b, c koeficienti in x spremenljivka, delimo obe strani s "sqrt (a ^ 2 + b ^ 2)":

`\\ frac a (sqrt (a ^ 2 + b ^ 2)) sin x +" \\ frac b (sqrt (a ^ 2 + b ^ 2)) cos x \u003d "\\ frac c (sqrt (a ^ 2 + b ^ 2)) `.

Koeficienti na levi strani imajo lastnosti sinusa in kosinusa, in sicer je vsota njihovih kvadratov enaka 1 in njihove absolutne vrednosti niso večje od 1. Označimo jih na naslednji način: `\\ frac a (sqrt (a ^ 2 + b ^ 2)) \u003d cos \\ varphi` , `\\ frac b (sqrt (a ^ 2 + b ^ 2)) \u003d sin \\ varphi`,` \\ frac c (sqrt (a ^ 2 + b ^ 2)) \u003d C`, potem:

`cos \\ varphi sin x + sin \\ varphi cos x \u003d C`.

Oglejmo si podrobneje naslednji primer:

Primer. Reši enačbo: `3 sin x + 4 cos x \u003d 2`.

Sklep. Razdelite obe strani enakosti s `sqrt (3 ^ 2 + 4 ^ 2)`, dobimo:

`\\ frac (3 sin x) (sqrt (3 ^ 2 + 4 ^ 2)) +" \\ frac (4 cos x) (sqrt (3 ^ 2 + 4 ^ 2)) \u003d "\\ frac 2 (sqrt (3 ^ 2 + 4 ^ 2)) `

`3/5 sin x + 4/5 cos x \u003d 2/5`.

Označimo `3/5 \u003d cos \\ varphi`,` 4/5 \u003d sin \\ varphi`. Ker je `sin \\ varphi\u003e 0`,` cos \\ varphi\u003e 0`, potem za pomožni kot vzamemo `\\ varphi \u003d arcsin 4/5`. Nato svojo enakost zapišemo v obliki:

`cos \\ varphi sin x + sin \\ varphi cos x \u003d 2 / 5`

Z uporabo formule za vsoto kotov sinusa zapišemo svojo enakost v naslednji obliki:

`sin (x + \\ varphi) \u003d 2 / 5`,

`x + \\ varphi \u003d (- 1) ^ n arcsin 2/5 + \\ pi n`,` n \\ v Z`,

`x \u003d (- 1) ^ n arcsin 2/5-` `arcsin 4/5 + \\ pi n`,` n \\ v Z`.

Odgovor. `x \u003d (- 1) ^ n arcsin 2/5-` `arcsin 4/5 + \\ pi n`,` n \\ v Z`.

Drobno-racionalne trigonometrične enačbe

To so enakosti z ulomki, katerih števci in imenovalci imajo trigonometrične funkcije.

Primer. Reši enačbo. `\\ frac (sin x) (1 + cos x) \u003d 1-cos x`.

Sklep. Pomnožite in delite desno stran enakosti z `(1 + cos x)`. Kot rezultat dobimo:

`\\ frac (sin x) (1 + cos x) \u003d" \\ frac ((1-cos x) (1 + cos x)) (1 + cos x) "

`\\ frac (sin x) (1 + cos x) \u003d" \\ frac (1-cos ^ 2 x) (1 + cos x) `

`\\ frac (sin x) (1 + cos x) \u003d" \\ frac (sin ^ 2 x) (1 + cos x) `

"\\ frac (sin x) (1 + cos x)-" \\ frac (sin ^ 2 x) (1 + cos x) \u003d 0 "

`\\ frac (sin x-sin ^ 2 x) (1 + cos x) \u003d 0`

Glede na to, da imenovalec ne more biti enak nič, dobimo `1 + cos x \\ ne 0`,` cos x \\ ne -1`, `x \\ ne \\ pi + 2 \\ pi n, n \\ v Z`.

Števec ulomka enačite z ničlo: `sin x-sin ^ 2 x \u003d 0`,` sin x (1-sin x) \u003d 0`. Potem je "sin x \u003d 0" ali "1-sin x \u003d 0".

1. `sin x \u003d 0`,` x \u003d \\ pi n`, `n \\ in Z`
2. `1-sin x \u003d 0`,` sin x \u003d -1`, `x \u003d \\ pi / 2 + 2 \\ pi n, n \\ in Z`.

Glede na to, da je "x \\ ne \\ pi + 2 \\ pi n, n \\ in Z`, so rešitve" x \u003d 2 \\ pi n, n \\ in Z` in "x \u003d \\ pi / 2 + 2 \\ pi n` , `n \\ v Z`.

Odgovor. `x \u003d 2 \\ pi n`,` n \\ v Z`, `x \u003d \\ pi / 2 + 2 \\ pi n`,` n \\ v Z`.

Trigonometrija in zlasti trigonometrične enačbe se uporabljajo na skoraj vseh področjih geometrije, fizike in tehnike. Študij se začne v 10. razredu, za izpit so zagotovo naloge, zato se poskusite spomniti vseh formul trigonometričnih enačb - vsekakor vam bodo prišle prav!

Vendar si jih niti ni treba zapomniti, glavno je razumeti bistvo in biti sposoben razbrati. Ni tako težko, kot se sliši. Prepričajte se sami tako, da si ogledate video.