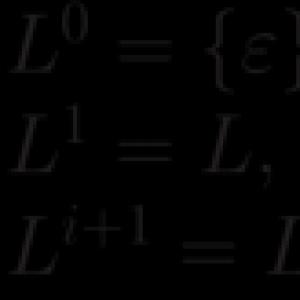Regulárne množiny a regulárne výrazy. Teória automatov a formálnych jazykov Abeceda, slovo, jazyk

Poznáme operácie kombinovania jazykov. Definujme operácie zreťazenia a iterácie (niekedy nazývané Kleene uzáver).

Nech L 1 a L 2 sú jazyky v abecede

Potom, t.j. jazykové zreťazenie pozostáva z zreťazení všetkých slov prvého jazyka so všetkými slovami druhého jazyka. Najmä ak , potom a ak , potom .

Predstavme si zápis pre „stupne“ jazyka L:

Teda L i zahŕňa všetky slová, ktoré možno rozdeliť na i po sebe idúce slová z L .

Iteráciu (L) * jazyka L tvoria všetky slová, ktoré možno rozdeliť na niekoľko po sebe idúcich slov z L:

Dá sa znázorniť pomocou stupňov:

Často je vhodné zvážiť „skrátenú“ iteráciu jazyka, ktorá neobsahuje prázdne slovo, ak v jazyku neexistuje: . Toto nie je nová operácia, ale jednoducho pohodlná skratka pre výraz .

Všimnite si tiež, že ak abecedu považujeme za konečný jazyk pozostávajúci z jednopísmenových slov, potom predtým zavedené označenie pre množinu všetkých slov, vrátane prázdnych slov, v abecede zodpovedá definícii iterácie tohto jazyka.

Nasledujúca tabuľka poskytuje formálnu induktívnu definíciu regulárne výrazy cez abecedu a jazyky, ktoré reprezentujú.

Výraz r	Jazyk L r
	L a = (a)
Nech je r 1 a r 2	L r1 a L r2 -reprezentovateľné
regulárne výrazy.	tie jazyky.
Potom nasledujúce výrazy
sú pravidelné	a predstavujú jazyky:
r=(r 1 + r 2)
r=(r 1 okruh 2)
r=(r 1) *	L r = L r1 *

Pri nahrávaní regulárne výrazy Vynecháme znak zreťazenia a predpokladáme, že operácia * má vyššiu prioritu ako zreťazenie a + a zreťazenie má vyššiu prioritu ako +. To umožní vynechať mnohé zátvorky. napr. možno zapísať ako 10(1 * + 0) .

Definícia 5.1. Dvaja regulárne výrazy r a p sa považujú za ekvivalentné, ak jazyky, ktoré reprezentujú, sú rovnaké, t.j. Lr = Lp. V tomto prípade píšeme r = p.

Je ľahké skontrolovať napríklad nasledovné vlastnosti pravidelného operácie:

• r + p = p + r (komutivita únie),
• (r+p) +q = r + (p+q) (asociatívnosť únie),
• (r p) q = r (p q) (asociatívnosť zreťazenia),
• (r *) * = r * (iteračná idempotencia),
• (r + p) q = rq + pq(distributivity).

Príklad 5.1. Ukážme ako príklad nie až tak samozrejmú rovnosť: (r + p) * = (r * p *) *.

Nech L 1 je jazyk reprezentovaný jeho ľavou stranou a L 2 jeho pravou stranou. Prázdne slovo patrí obom jazykom. Ak je slovo neprázdne, potom podľa definície iterácie môže byť reprezentované ako zreťazenie podslov patriacich do jazyka. Ale tento jazyk je podmnožinou jazyka L"=L r * L p * (prečo?). Preto . Naopak, ak slovo , potom je reprezentovateľné ako zreťazenie podslov patriacich do jazyka L". Každé z takýchto podslov v je reprezentovateľné v tvare v= v 1 1 ... v k 1 v 1 2 ... v l 2

, kde pre všetky i=1, ... , k je podslovo a pre všetky j=1, ... , l je podslovo (je možné, že k alebo l sa rovná 0). To však znamená, že w je zreťazením podslov, z ktorých každé patrí do a teda .Pravidelné sady

, kde pre všetky i=1, ... , k je podslovo a pre všetky j=1, ... , l je podslovo (je možné, že k alebo l sa rovná 0). To však znamená, že w je zreťazením podslov, z ktorých každé patrí do a teda .

a regulárne výrazy

V tejto časti budeme uvažovať o triede množín reťazcov nad konečným slovníkom, ktoré sa dajú veľmi ľahko opísať nejakými vzorcami. Tieto sady sa nazývajú pravidelné.Definícia 1. Nechaj V 1 A V 2 -veľa reťazcov. Definujme tri operácie

na týchto súpravách.

Spojenie: V 1 V 2 =(|   V 1 ) alebo   V 2 .

Reťazenie (produkt, lepenie): Vl V2 = (|  V 1 ,  V 2 ) Znak operácie zreťazenia sa zvyčajne vynecháva. Príklad:

V, = (abc, ba), V2 = (b, cb). V1V2 = (abcb, abccb, bab, bacb).

Reťazenie (produkt, lepenie): Vl V2 = (|  V 1 ,  V 2 ) Znak operácie zreťazenia sa zvyčajne vynecháva. Označme V n súčin n množín V:V n =VV...V,V° =() (tu je  prázdny reťazec).

V 1 = (abc, ba), V 1 2 = (abcabc, abcba, baba, baabc).

Reťazenie (produkt, lepenie): Vl V2 = (|  V 1 ,  V 2 ) Znak operácie zreťazenia sa zvyčajne vynecháva. 3. Iterácia: V* = V 0 V 1 V 2 ... =   =0 ∞ V n .

V = (a, bc), V* = (, a, bc, aa, abc, bcbc, bca, aaa, aabc,...).Definícia 4.13. Trieda pravidelných množín nad konečným slovníkom Vdefinovať

ide takto:

odbor ST;

ST zreťazenie;

iteráciu S* a T*.

5. Ak množinu nemožno zostrojiť konečným použitím pravidiel 1-4, potom je nepravidelná.

Príklady pravidelných množín: (ab, ba)* (aa); (b) ((c)(d, ab)*). Príklady nepravidelných množín: (a n b n | n > 0); ( | v reťazci  sa počet výskytov symbolov a a b zhoduje).

Regulárne výrazy

Regulárne množiny sú dobré, pretože sa dajú veľmi jednoducho opísať pomocou vzorcov, ktoré budeme nazývať regulárne výrazy.Definícia 2. Trieda pravidelných množín nad konečným slovníkom Vdefinovať

Trieda regulárneho výrazu nad konečným slovníkom

ich súčet R1+R2;

ich produkt R1R2;

ich opakovanie R1* a R2*.

Pracovný symbol možno vynechať. Na zníženie počtu zátvoriek sa ako v každej algebre používajú priority operácií: iterácia má najvyššiu prioritu; práca má menšiu prioritu; sčítanie má najnižšiu prioritu.

Príklady regulárnych výrazov: ab + bа*; (aa)*b + (c + dab)*.

Je zrejmé, že regulárne množiny a regulárne výrazy sú si veľmi blízke. Predstavujú však rôzne entity: pravidelná množina je množina reťazcov (vo všeobecnom prípade nekonečná) a regulárny výraz jevzorec schematicky znázorňujúci, ako bola vytvorená zodpovedajúca regulárna množina pomocou operácií uvedených vyššie(a tento vzorec je konečný).

Nech R^ je regulárna množina zodpovedajúca regulárnemu výrazu R. Potom:

Regulárny výraz je teda konečný vzorec, ktorý definuje nekonečný počet reťazcov, teda jazyk.

Pozrime sa na príklady regulárnych výrazov a im zodpovedajúcich jazykov.

Regulárny výraz	Zodpovedajúci jazyk
	Všetky reťazce začínajúce na b, za ktorými nasleduje ľubovoľný počet znakov a
	Všetky reťazce aab obsahujúce práve dva výskyty b
	Všetky reťazce a a b, v ktorých sa symboly b vyskytujú iba v pároch
(a+b)*(aa+bb)(a+b)*	Všetky reťazce a a b obsahujúce aspoň jeden pár susediacich a alebo b
(0+1)*11001(0+1)*	Všetky reťazce 0 a 1 obsahujúce podreťazec 11001
	Všetky reťazce a a b, začínajúce a a končiace b

Je zrejmé, že množina reťazcov je regulárna vtedy a len vtedy, ak ju možno reprezentovať regulárnym výrazom. Rovnaká množina reťazcov však môže byť reprezentovaná rôznymi regulárnymi výrazmi, napríklad množina reťazcov pozostávajúca zo symbolov a a obsahujúca aspoň dve a môže byť reprezentovaná výrazmi: aa*a; a*aaa*; aaa*; a*aa*aa* atď.

Definícia 3.Dva regulárne výrazy R1 V 1 R2 sa nazývajú ekvivalentné (označené Rl = R2) vtedy a len vtedyR1 ^ = R2 ^ .

Teda aa*a = a*aaa* = aaa* = a*aa*aa*. Vynára sa otázka, ako určiť ekvivalenciu dvoch regulárnych výrazov.

Veta1 . Pre akékoľvek regulárne výrazy R, S V 1 T spravodlivý:

Tieto vzťahy možno dokázať kontrolou rovnosti zodpovedajúcich množín reťazcov. Môžu byť použité na zjednodušenie regulárnych výrazov. Napríklad: b (b + aa*b) = b (b + aa*b) = b ( + aa*) b = ba*b. Preto b (b + aa*b) = ba*b, čo nie je zrejmé.

Kleeneho veta

Regulárne výrazy sú konečné vzorce, ktoré definujú regulárne jazyky. Ale podobnú vlastnosť majú aj konečné automaty – tiež definujú jazyky. Vynára sa otázka: ako spolu súvisia triedy jazykov definované konečnými automatmi a regulárnymi výrazmi? Označme A mnoho automatických jazykov, R je množina regulárnych jazykov. Stephen Kleene, americký matematik, dokázal nasledujúcu vetu.

Veta2 . (Kleenova veta.) Triedy regulárnych množín a automatových jazykov sa zhodujú, tzn A = R .

Inými slovami, každý jazyk automatov môže byť špecifikovaný vzorcom (regulárnym výrazom) a každá regulárna množina môže byť rozpoznaná konečným automatom. Túto vetu dokážeme konštruktívne v dvoch krokoch. V prvom kroku dokážeme, že každý jazyk automatu je regulárna množina (alebo, čo je to isté, pre každý konečný automat môžeme zostrojiť regulárny výraz, ktorý špecifikuje jazyk, ktorý tento automat rozpoznáva). V druhom kroku dokážeme, že každá regulárna množina je jazykom automatov (alebo, čo je to isté, z akéhokoľvek regulárneho výrazu sa dá zostrojiť konečný automat, ktorý pripúšťa presne reťazce zodpovedajúcej regulárnej množiny).

Predstavme si model prechodového grafu ako zovšeobecnenie modelu konečného automatu. Prechodový graf má jeden počiatočný a ľubovoľný počet koncových vrcholov a orientované hrany sú na rozdiel od konečného automatu označené nie symbolmi, ale regulárnymi výrazmi. Prechodový graf pripúšťa reťazec a if A patrí do množiny reťazcov, opísaných súčinom regulárnych výrazov R 1 R 2 ...R n , ktoré označujú cestu z počiatočného vrcholu do jedného z koncových vrcholov. Množina reťazcov povolená grafom prechodu tvorí jazyk, ktorý umožňuje.

Ryža. 1. Prechodový graf

Na obr. Obrázok 1 ukazuje graf prechodu, ktorý umožňuje napríklad reťazec abbca, keďže cesta s->r->p->s->r->q, ktorá vedie ku konečnému stavu q, je označená reťazcom regulárne výrazy ab* c*a. Konečný automat je špeciálny prípad prechodového grafu, a preto všetky jazyky, ktoré stavové automaty akceptujú, sú podporované aj prechodovými grafmi.

Veta 3.Každý jazyk automatu je regulárna množina, A  R.

Dôkaz. Prechodový graf s jedným začiatočným a jedným koncovým vrcholom, v ktorom je jediná hrana z počiatočného do koncového vrcholu označená regulárnym výrazom R, pripúšťa jazyk R^ (obr. 1).

Ryža. 2. Prechodový graf pripúšťajúci regulárny jazyk FT

Dokážme teraz, že každý jazyk automatu je regulárna množina zmenšením akéhokoľvek grafu prechodu bez zmeny jazyka, ktorý umožňuje, na ekvivalentnú formu (obr. 2).

Akýkoľvek konečný automat a akýkoľvek prechodový graf je možné vždy znázorniť v normalizovanej forme, v ktorej je len jeden počiatočný vrchol len s výstupnými hranami a len jeden koncový vrchol len so vstupnými hranami (obr. 3).

Ryža. 3. Prechodový graf s jedným počiatočným a jedným konečným vrcholom

S prechodovým grafom prezentovaným v normalizovanej forme je možné vykonať dve operácie redukcie – redukciu hrán a redukciu vrcholov – pri zachovaní jazyka povoleného týmto prechodovým grafom:

a) redukcia rebier:

B ) redukcia vrcholu (nahradenie sa vykoná pre každú cestu prechádzajúcu cez vrchol p, po ktorej nasleduje jej vyradenie ako nedosiahnuteľný stav):

Je zrejmé, že každá operácia redukcie nemení jazyk rozpoznávaný prechodovým grafom, ale znižuje buď počet hrán alebo počet vrcholov, a nakoniec redukcie privedú prechodový graf do podoby znázornenej na obr. 2. Veta je dokázaná: každý jazyk automatu je regulárna množina.

Príklad

Nech je daný konečný stroj A:

Zostrojíme ekvivalentný prechodový graf v normalizovanej forme.

Zmenšenie vertexu 3:

Zmenšenie oblúkov a použitie pravidla R = R:

Zmenšenie vertexu 2:

Zmenšenie oblúka a vrcholu 1:

Jazyk rozpoznávaný automatom A je teda daný regulárnym výrazom: R A = b+(a+bb)(b+ab)*a.

Dokážme Kleeneovu vetu v opačnom smere.

Veta 2.Každá regulárna množina je jazyk automatu: R A.

Dôkaz. Ukážme, že pre každý regulárny výraz R možno zostrojiť konečný automat A r (prípadne nedeterministický), ktorý rozpoznáva jazyk špecifikovaný R. Takéto automaty zadefinujeme rekurzívne.

(počiatočný a konečný stav A sú kombinované).

Príklad(pokračovanie)

Bežný jazyk

V teórii jazyka bežná sada(alebo, v bežnom jazyku) sa nazýva formálny jazyk, ktorý spĺňa nasledujúce vlastnosti. Tieto jednoduché vlastnosti sú také, že triedu regulárnych množín je vhodné študovať ako celok a získané výsledky sú použiteľné v mnohých dôležitých prípadoch formálnych jazykov. To znamená, že koncept pravidelnej množiny je príkladom matematickej štruktúry.

Definícia regulárnej množiny

Nech Σ je konečná abeceda. Bežná súprava R(Σ) v abecede Σ je definované nasledujúcimi rekurzívnymi vlastnosťami:

№.	Nehnuteľnosť	Popis
1		Prázdna množina je pravidelná množina v abecede Σ
2		Množina pozostávajúca iba z jedného prázdneho reťazca je pravidelná množina v abecede Σ
3		Množina pozostávajúca z ľubovoľného jedného symbolu abecedy Σ je pravidelná množina v abecede Σ
4		Ak sú ľubovoľné dve množiny regulárne v abecede Σ, ich spojenie je tiež regulárnou množinou v abecede Σ
5		Ak sú ľubovoľné dve množiny regulárne v abecede Σ, potom množina zložená zo všetkých možných kombinácií dvojíc ich prvkov je tiež regulárnou množinou v abecede Σ
6		Ak je ľubovoľná množina regulárnej v abecede Σ, potom množina všetkých možných kombinácií jej prvkov je tiež regulárnou množinou v abecede Σ
		Nič iné ako nasledujúce nie je pravidelná množina v abecede Σ

Pozri tiež

• Vytvorenie syntaktického analyzátora založeného na automatizovanom prístupe

Nadácia Wikimedia.

2010.

Pozrite si, čo je „Normálny jazyk“ v iných slovníkoch: regulárny jazyk - - Telekomunikačné témy, základné pojmy EN regulárny jazyk...

Technická príručka prekladateľa - (lat. regularius, z regula rule). Správne, správne usporiadané, vyrobené. Pravidelný chod stroja. Dokonca aj mŕtvica. Pravidelný život. Správny, slušný, monotónny život. Slovník cudzích slov zahrnutých v ruskom jazyku... ...

Slovník cudzích slov ruského jazyka Cm…

Slovník synoným Staroveký písaný jazyk - Jazyk s dlhými písomnými tradíciami, to znamená, že pred niekoľkými storočiami dostal spisovný jazyk prispôsobený štruktúre daného jazyka a fungovanie spisovnej verzie jazyka nebolo epizodické, ale pravidelné, s... . ..

Slovník sociolingvistických pojmov

Tento výraz má iné významy, pozri kečuánčinu. Quechua Vlastné meno: Qhichwa Simi, Runa Simi Countries ... Wikipedia Rám budovy s rastrom stĺpov alebo stĺpikov založených na schode rovnakej veľkosti (bulharčina; Български) jednotná kostra (čeština; čeština) Pravidelná kostra (nemčina; nemčina) regelmäßiges Skelett (maďarčina; maďarčina) szabályos... ...

Stavebný slovník Rám budovy s rastrom stĺpov alebo stĺpikov založených na schode rovnakej veľkosti (bulharčina; Български) jednotná kostra (čeština; čeština) Pravidelná kostra (nemčina; nemčina) regelmäßiges Skelett (maďarčina; maďarčina) szabályos... ...

Quechua Vlastné meno: Qhichwa Simi, Runa Simi Krajiny: Argentína, Bolívia, Kolumbia, Peru, Čile, Ekvádor Regióny: Andy Oficiálny status: Peru ... Wikipedia

Tagalogský jazyk- (tagal, tagala, tagalo; tagalog) jeden z filipínskych jazykov. Oblasť počiatočnej distribúcie je v politicky, ekonomicky a kultúrne najvýznamnejšom regióne Filipínskej republiky - strednej a južnej časti ostrova... ... Lingvistický encyklopedický slovník

knihy

• Odvodené slovesá. Tajomstvo fínskej gramatiky. Učebnica, Safronov V.D.. Príručka je venovaná jednej z najzaujímavejších a nedostatočne prezentovaných sekcií fínskej gramatiky v ruskojazyčnej náučnej literatúre - odvodeným slovesám. Tvoria sa zo slovies a z mien...

Laboratórna práca č.3

Vývoj lexikálneho analyzátora je pomerne jednoduchý, ak sa použije teória regulárnych jazykov a konečných automatov. V rámci tejto teórie sa triedy lexém rovnakého typu považujú za formálne jazyky (jazyk identifikátorov, jazyk konštánt atď.), ktorých množina viet je opísaná pomocou zodpovedajúcej generatívnej gramatiky. Okrem toho sú tieto jazyky také jednoduché, že ich generuje najjednoduchšia gramatika - pravidelná gramatika.

Definícia 1. generatívna gramatika G = , ktorého pravidlá majú tvar: A::=aB alebo C::=b, kde A, B, C Є N; a, b Є Т sa nazýva pravidelné (automatické).

Jazyk L (G) generovaný automatovou gramatikou sa nazýva automatový (regulárny) jazyk alebo jazyk s konečným počtom stavov.

Príklad 1. Trieda identifikátorov, ak je identifikátorom postupnosť pozostávajúca z písmen a číslic a prvý znak identifikátora môže byť iba písmeno, je opísaná nasledujúcou generatívnou regulárnou gramatikou G = , v ktorom

N = (I, K), T = (b, c), S = (I),

P = (1. I::= b

Tu b, c sú zovšeobecnené koncové symboly na označenie písmen a číslic.

Proces generovania identifikátora „bbcbc“ je opísaný nasledujúcou postupnosťou substitúcií

I => bbc => bbc => bbcK => bbcbK => bbcbc

Hlavnou úlohou LA však nie je generovanie lexikálnych jednotiek, ale ich rozpoznávanie. Matematickým modelom procesu rozpoznávania regulárneho jazyka je výpočtové zariadenie nazývané konečný automat (FA). Pojem „konečný“ zdôrazňuje, že výpočtové zariadenie má pevné a konečné množstvo pamäte a spracováva sekvenciu vstupných symbolov patriacich do nejakej konečnej množiny. Existujú rôzne typy KA, ak výstupná funkcia KA (výsledok práce) je len indikáciou, či je vstupná sekvencia symbolov akceptovateľná alebo nie, takáto KA sa nazýva konečný riešiteľ.

Definícia 2. Nasledujúcich päť sa nazýva konečný automat:

A = , kde V = (a 1 , a 2 , …, a m ) – vstupná abeceda (konečná množina symbolov);

Q = (q 0 , q 1 , …, q n -1 ) – abeceda stavov (konečná množina symbolov);

δ: Q ×V →Q – prechodová funkcia;

q 0 Є Q – počiatočný stav konečného automatu;

F Є Q – súbor konečných stavov.

Prevádzková schéma kozmickej lode.

Existuje nekonečná páska, rozdelená na bunky, z ktorých každá môže obsahovať jeden symbol z V. Na páske je napísaný reťazec α Є V*. Bunky naľavo a napravo od reťazca sú prázdne. K dispozícii je koncové ovládacie zariadenie (FCU) s čítacou hlavou, ktorá môže postupne čítať znaky z pásky, pričom sa pohybuje pozdĺž pásky zľava doprava. V tomto prípade môže byť riadiaca jednotka v akomkoľvek stave od Q. Riadiaca jednotka vždy začína svoju prácu v počiatočnom stave q 0 a končí v jednom z konečných stavov F. Zakaždým, keď sa presuniete do novej bunky na páska, riadiaca jednotka prejde do nového stavu v súlade s funkciou δ.

Prechodová funkcia kozmickej lode môže byť reprezentovaná nasledujúcimi spôsobmi:

· Súbor tímov;

· Stavový diagram;

· Prechodová tabuľka.

Príkaz stavového automatu je napísaný takto:

(q i, a j) → q k, kde q i, q k Є Q; a j Є V.

Tento príkaz znamená, že stavový automat je v stave q i, načíta symbol a j z pásky a prejde do stavu q k.

Graficky je príkaz znázornený ako oblúk grafu idúci z vrcholu q i do vrcholu q k a označený symbolom a j vstupnej abecedy:

Grafické znázornenie celého zobrazenia δ sa nazýva stavový diagram konečného automatu.

Ak sa kozmická loď ocitne v situácii (q i, a j), ktorá nie je ľavou stranou žiadneho príkazu, potom sa zastaví. Ak riadiaca jednotka spočíta všetky symboly reťazca α zaznamenané na páske a zároveň prejde do konečného stavu q r Є F, potom hovorí, že reťazec α je povolený automatom konečných stavov.

Prechodová tabuľka kozmickej lode je skonštruovaná nasledovne: stĺpce matice zodpovedajú symbolom zo vstupnej abecedy, riadky zodpovedajú symbolom zo stavovej abecedy a prvky matice zodpovedajú stavom, do ktorých sa kozmická loď dostane pre danú kombináciu vstupného symbolu. a štátny symbol.

Nech pravidelná gramatika G = , ktorého pravidlá majú tvar: A i::= a j A k alebo A i::= a j, kde A i, Ak Є N a a j Є T.

Potom konečný automat A = , ktorý pripúšťa rovnaký jazyk, aký generuje regulárna gramatika G, je skonštruovaný takto:

2) Q = N U (Z), Z N a Z T, Z je konečný stav kozmickej lode;

5) Zobrazenie δ je skonštruované v tvare:

· Každé substitučné pravidlo v gramatike G tvaru A i::= a j Ak je spojené s príkazom (A i, a j) → Ak;

· Každé substitučné pravidlo tvaru A i::= a j je spojené s príkazom (A i, a j) → Z;

Príklad 2 Zostrojte CA pre gramatiku z príkladu 1. Máme A = , Kde

1) V = T = (b, c)

2) Q = NU (Z) = (I, R, Z)

3) q 0 = (S) = (I)

5) δ: a) vo forme súboru príkazov:

b) vo forme stavového diagramu

Existujú deterministické a nedeterministické konečné automaty. Kozmická loď je tzv nedeterministický KA (NKA), ak v jeho stavovom diagrame vychádza z jedného vrcholu niekoľko oblúkov s identickými značkami. Napríklad KA z príkladu 2 je NKA.

Pre praktické účely je potrebné, aby konečný rozpoznávač sám určil moment ukončenia vstupnej sekvencie znakov a vydal správu o správnosti alebo chybe vstupnej sekvencie. Na tieto účely sa vstupný reťazec považuje za obmedzený vpravo koncovou značkou ├ a interpretované stavy sa zapisujú do stavového diagramu kozmickej lode:

Z – „povoliť vstupný reťazec“;

O – „vo vstupnom reťazci bola zapamätaná chyba“;

E – „odmietnuť vstupný reťazec“.

Stavy Z a E sú konečné a kozmická loď k nim prejde pri čítaní koncovej značky ├ po spracovaní správneho alebo chybného vstupného reťazca. Stav O je prechodný, kozmická loď sa do neho presunie z akéhokoľvek platného stavu kozmickej lode, keď sa zistí chyba vo vstupnom reťazci a zostane tam, kým nepríde koncová značka ├, po ktorej prejde do stavu E – „odmietnuť vstupný reťazec. “