Pagrindinis tyrimas. Didžioji Ferma teorema Kodėl jie negali įrodyti Ferma teoremos?
2013 m. rugpjūčio 5 d
Pasaulyje nėra daug žmonių, kurie niekada nėra girdėję apie Paskutinę Ferma teoremą - galbūt tai vienintelė matematinė problema, kuri tapo taip plačiai žinoma ir tapo tikra legenda. Jis minimas daugelyje knygų ir filmų, o pagrindinis beveik visų paminėjimų kontekstas yra teoremos įrodyti neįmanoma.
Taip, ši teorema yra labai gerai žinoma ir tam tikra prasme tapo „stabu“, kurį garbina matematikai mėgėjai ir profesionalai, tačiau mažai kas žino, kad jos įrodymas buvo rastas, ir tai įvyko dar 1995 m. Bet pirmiausia pirmiausia.
Taigi paskutinė Ferma teorema (dažnai vadinama paskutine Ferma teorema), kurią 1637 m. suformulavo genialus prancūzų matematikas Pierre'as Fermat, iš esmės yra labai paprasta ir suprantama visiems, turintiems vidurinį išsilavinimą. Sakoma, kad formulė a n laipsnio + b laipsnio n = c laipsnio n neturi natūralių (ty ne trupmeninių) sprendinių, kai n > 2. Viskas atrodo paprasta ir aišku, bet Geriausi matematikai ir paprasti mėgėjai ieškojo sprendimo daugiau nei tris su puse amžiaus.
Kodėl ji tokia garsi? Dabar išsiaiškinsime...
Ar yra daug įrodytų, neįrodytų ir dar neįrodytų teoremų? Esmė ta, kad paskutinė Ferma teorema yra didžiausias kontrastas tarp formuluotės paprastumo ir įrodymo sudėtingumo. Paskutinė Ferma teorema yra neįtikėtinai sudėtinga problema, tačiau jos formuluotę gali suprasti kiekvienas, baigęs 5-tą vidurinės mokyklos klasę, tačiau net ne kiekvienas profesionalus matematikas gali suprasti įrodymą. Nei fizikoje, nei chemijoje, nei biologijoje, nei matematikoje nėra nė vienos problemos, kurią būtų galima taip paprastai suformuluoti, bet taip ilgai liko neišspręsta. 2. Iš ko jis susideda?
Pradėkime nuo pitagoriečių kelnių.Formuluotė tikrai paprasta – iš pirmo žvilgsnio. Kaip žinome nuo vaikystės, „Pitagoro kelnės yra vienodos iš visų pusių“. Užduotis atrodo tokia paprasta, nes ji buvo pagrįsta matematiniu teiginiu, kurį visi žino – Pitagoro teorema: bet kuriame stačiakampiame trikampyje ant hipotenuzės pastatytas kvadratas yra lygus kvadratų, pastatytų ant kojų, sumai.
V amžiuje prieš Kristų. Pitagoras įkūrė pitagoriečių broliją. Pitagoriečiai, be kita ko, tyrinėjo sveikųjų skaičių trynukus, tenkinančius lygybę x²+y²=z². Jie įrodė, kad yra be galo daug Pitagoro trigubų ir gavo bendras jų radimo formules. Tikriausiai jie bandė ieškoti C ir aukštesnių laipsnių. Įsitikinę, kad tai nepavyko, pitagoriečiai atsisakė savo nenaudingų bandymų. Brolijos nariai buvo daugiau filosofai ir estetai nei matematikai.

Tai yra, nesunku pasirinkti skaičių rinkinį, kuris puikiai tenkintų lygybę x²+y²=z²
Pradedant nuo 3, 4, 5 - iš tikrųjų jaunesnysis studentas supranta, kad 9 + 16 = 25.
Arba 5, 12, 13: 25 + 144 = 169. Puiku.
Taigi, pasirodo, kad jų NĖRA. Čia ir prasideda triukas. Paprastumas yra akivaizdus, nes sunku įrodyti ne kažko buvimą, o, priešingai, jo nebuvimą. Kai reikia įrodyti, kad sprendimas yra, galite ir turėtumėte tiesiog pateikti šį sprendimą.
Įrodyti nebuvimą yra sunkiau: pavyzdžiui, kažkas sako: tokia ir tokia lygtis neturi sprendinių. Įmesti jį į balą? lengva: bam – ir štai, sprendimas! (pateikti sprendimą). Ir viskas, priešininkas nugalėtas. Kaip įrodyti nebuvimą?
Sakykite: „Aš neradau tokių sprendimų“? O gal neblogai atrodai? O jei jie egzistuoja, tik labai dideli, labai dideli, tokie, kad net itin galingam kompiuteriui vis tiek neužtenka jėgų? Štai kas sunku.
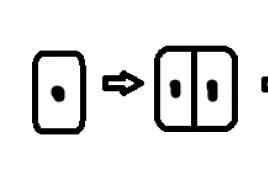
Tai galima vaizdžiai parodyti taip: jei paimsite du tinkamo dydžio kvadratus ir išardysite juos į vienetinius kvadratus, tada iš šios vienetinių kvadratų krūvos gausite trečią kvadratą (2 pav.): 
Bet padarykime tą patį su trečiuoju matmeniu (3 pav.) - jis neveikia. Nepakanka kubelių arba liko papildomų:

Tačiau XVII amžiaus matematikas prancūzas Pierre'as de Fermat entuziastingai tyrinėjo bendrąją lygtį x n + y n = z n. Ir galiausiai padariau išvadą: n>2 sveikųjų skaičių sprendinių nėra. Fermato įrodymas negrįžtamai prarastas. Rankraščiai dega! Liko tik jo pastaba Diofanto „Aritmetikoje“: „Radau tikrai nuostabų šio teiginio įrodymą, bet paraštės čia per siauros, kad jį sutilpčiau“.
Tiesą sakant, teorema be įrodymo vadinama hipoteze. Tačiau Fermatas garsėja kaip niekada neklysta. Net jei jis nepaliko pareiškimo įrodymų, vėliau tai buvo patvirtinta. Be to, Fermatas įrodė savo tezę n=4. Taigi prancūzų matematiko hipotezė įėjo į istoriją kaip paskutinė Ferma teorema.

Po Fermato tokie puikūs protai kaip Leonhardas Euleris dirbo ieškodami įrodymų (1770 m. jis pasiūlė n = 3 sprendimą),

Adrien Legendre ir Johann Dirichlet (šie mokslininkai kartu rado n = 5 įrodymą 1825 m.), Gabrielis Lamé (kuris rado n = 7 įrodymą) ir daugelis kitų. Praėjusio amžiaus 80-ųjų viduryje tapo aišku, kad mokslo pasaulis artėja prie galutinio Ferma'o teoremos sprendimo, tačiau tik 1993 m. matematikai pamatė ir patikėjo, kad trijų šimtmečių epas ieškojo įrodymo. Paskutinė Fermato teorema praktiškai baigėsi.
Lengvai parodoma, kad pakanka įrodyti Ferma teoremą tik paprastam n: 3, 5, 7, 11, 13, 17, ... Sudėtiniam n įrodymas lieka galioti. Tačiau pirminių skaičių yra be galo daug...
1825 m., naudodamos Sophie Germain metodą, moterys matematikės, Dirichlet ir Legendre nepriklausomai įrodė teoremą, kai n=5. 1839 m., naudodamas tą patį metodą, prancūzas Gabrielis Lame'as parodė teoremos teisingumą, kai n=7. Palaipsniui teorema buvo įrodyta beveik visiems n mažiau nei šimtas.

Galiausiai vokiečių matematikas Ernstas Kummeris, atlikęs puikų tyrimą, parodė, kad teorema apskritai negali būti įrodyta naudojant XIX amžiaus matematikos metodus. 1847 metais už Ferma teoremos įrodymą įsteigta Prancūzijos mokslų akademijos premija liko neįteikta.

1907 m. turtingas vokiečių pramonininkas Paulas Wolfskehlas dėl nelaimingos meilės nusprendė atimti gyvybę. Kaip tikras vokietis, jis nustatė savižudybės datą ir laiką: tiksliai vidurnaktį. Paskutinę dieną jis sudarė testamentą ir parašė laiškus draugams ir artimiesiems. Reikalai baigėsi prieš vidurnaktį. Reikia pasakyti, kad Paulius domėjosi matematika. Neturėdamas ką veikti, jis nuėjo į biblioteką ir pradėjo skaityti garsųjį Kummerio straipsnį. Staiga jam atrodė, kad Kummeris suklydo savo samprotavimuose. Wolfskelis pradėjo analizuoti šią straipsnio dalį su pieštuku rankose. Praėjo vidurnaktis, atėjo rytas. Įrodymų spraga užpildyta. Ir pati savižudybės priežastis dabar atrodė visiškai juokingai. Paulius suplėšė atsisveikinimo laiškus ir perrašė testamentą.
Netrukus jis mirė dėl natūralių priežasčių. Įpėdiniai buvo gerokai nustebinti: 100 000 markių (daugiau nei 1 000 000 dabartinių svarų sterlingų) buvo pervesta į Getingeno karališkosios mokslo draugijos sąskaitą, kuri tais pačiais metais paskelbė konkursą Wolfskehlio premijai gauti. 100 000 markių buvo skirta asmeniui, kuris įrodė Ferma teoremą. Už teoremos paneigimą nebuvo apdovanotas nė pfenigas...
Dauguma profesionalių matematikų laikė paskutinės Ferma teoremos įrodymo paiešką beviltiška užduotimi ir ryžtingai atsisakė gaišti laiką tokiam nenaudingam pratimui. Tačiau mėgėjams buvo smagu. Praėjus kelioms savaitėms po paskelbimo Getingeno universitetą užgriuvo „įkalčių“ lavina. Profesorius E.M. Landau, kurio pareiga buvo išanalizuoti atsiųstus įrodymus, išdalino savo studentams korteles:
Gerb. . . . . . . .
Ačiū, kad atsiuntėte man rankraštį su paskutinės Ferma teoremos įrodymu. Pirma klaida yra puslapyje ... eilutėje... . Dėl to visas įrodymas praranda galiojimą.
Profesorius E. M. Landau


1963 metais Paulas Cohenas, remdamasis Gödelio išvadomis, įrodė vienos iš dvidešimt trijų Hilberto problemų – kontinuumo hipotezės – neišsprendžiamumą. O kas, jei paskutinė Ferma teorema taip pat neišsprendžiama?! Tačiau tikri Didžiosios teoremos fanatikai nė kiek nenusivylė. Kompiuterių atsiradimas matematikams netikėtai suteikė naują įrodinėjimo metodą. Po Antrojo pasaulinio karo programuotojų ir matematikų komandos įrodė paskutinę Fermato teoremą visoms n reikšmėms iki 500, vėliau iki 1000, o vėliau iki 10000.
Devintajame dešimtmetyje Samuelis Wagstaffas padidino ribą iki 25 000, o 1990-aisiais matematikai paskelbė, kad paskutinė Ferma teorema yra teisinga visoms n vertėms iki 4 mln. Bet jei iš begalybės atimsi net trilijoną trilijoną, ji netaps mažesnė. Matematikos neįtikina statistika. Įrodyti Didžiąją teoremą reiškė įrodyti ją VISIEMS n iki begalybės.

1954 metais du jauni draugai japonai matematikai pradėjo tyrinėti modulines formas. Šios formos generuoja skaičių serijas, kurių kiekviena turi savo eilutes. Atsitiktinai Taniyama palygino šias serijas su elipsinėmis lygtimis sugeneruotomis serijomis. Jie sutapo! Tačiau modulinės formos yra geometriniai objektai, o elipsinės lygtys yra algebrinės. Niekada nebuvo rastas ryšys tarp tokių skirtingų objektų.
Tačiau po kruopštaus patikrinimo draugai iškėlė hipotezę: kiekviena elipsinė lygtis turi dvynį – modulinę formą ir atvirkščiai. Būtent ši hipotezė tapo visos matematikos krypties pagrindu, tačiau kol nebuvo įrodyta Taniyama-Shimura hipotezė, visas pastatas bet kurią akimirką gali sugriūti.
1984 m. Gerhardas Frey'us parodė, kad Ferma lygties sprendimas, jei toks yra, gali būti įtrauktas į kokią nors elipsinę lygtį. Po dvejų metų profesorius Kenas Ribetas įrodė, kad ši hipotetinė lygtis negali turėti atitikmens moduliniame pasaulyje. Nuo šiol paskutinė Ferma teorema buvo neatsiejamai susijusi su Taniyama-Shimura spėjimu. Įrodžius, kad bet kuri elipsinė kreivė yra modulinė, darome išvadą, kad nėra elipsės lygties su Ferma lygties sprendimu, ir paskutinė Ferma teorema būtų įrodyta iš karto. Tačiau trisdešimt metų nepavyko įrodyti Taniyama-Shimura hipotezės, o sėkmės buvo vis mažiau.
1963 m., būdamas vos dešimties metų, Andrew Wilesas jau susižavėjo matematika. Sužinojęs apie Didžiąją teoremą, jis suprato, kad negali jos atsisakyti. Būdamas moksleivis, studentas ir abiturientas, jis ruošėsi šiai užduočiai.
Sužinojęs apie Keno Ribeto išvadas, Wilesas stačia galva pasinėrė į Taniyama-Shimura hipotezės įrodymą. Jis nusprendė dirbti visiškai izoliuotas ir slaptas. „Supratau, kad viskas, kas turi ką nors bendro su paskutine Ferma teorema, sukelia per didelį susidomėjimą... Per daug žiūrovų akivaizdžiai trukdo siekti tikslo. Septyneri sunkaus darbo metai atsipirko, Wilesas pagaliau užbaigė Taniyama-Shimura spėlionių įrodymą.
1993 m. anglų matematikas Andrew Wilesas pristatė pasauliui savo paskutinės Ferma teoremos įrodymą (Wilesas perskaitė savo sensacingą pranešimą konferencijoje Sir Isaac Newton institute Kembridže.), kurio darbas truko daugiau nei septynerius metus.
Kol ažiotažas tęsėsi spaudoje, buvo pradėtas rimtas darbas tikrinant įrodymus. Kiekvienas įrodymas turi būti atidžiai išnagrinėtas, kad įrodymai būtų laikomi griežtais ir tiksliais. Wilesas praleido neramią vasarą laukdamas atsiliepimų iš apžvalgininkų, tikėdamasis, kad jam pavyks susilaukti jų pritarimo. Rugpjūčio pabaigoje ekspertai nuosprendį pripažino nepakankamai pagrįstu.
Paaiškėjo, kad šiame sprendime yra šiurkšti klaida, nors apskritai jis yra teisingas. Wilesas nepasidavė, į pagalbą pasikvietė garsųjį skaičių teorijos specialistą Richardą Taylorą ir jau 1994 metais paskelbė pataisytą ir išplėstą teoremos įrodymą. Nuostabiausia, kad šis darbas matematikos žurnale „Matematikos metraštis“ užėmė net 130 (!) puslapių. Tačiau istorija tuo taip pat nesibaigė - galutinis taškas buvo pasiektas tik kitais metais, 1995 m., Kai buvo paskelbta galutinė ir „ideali“, matematiniu požiūriu, įrodymo versija.
„...praėjus pusei minutės nuo šventinės vakarienės jos gimtadienio proga, įteikiau Nadjai pilno įrodymo rankraštį“ (Andrew Wales). Ar aš dar nesakiau, kad matematikai yra keisti žmonės?

Šį kartą dėl įrodymų nekilo jokių abejonių. Du straipsniai buvo kruopščiai išanalizuoti ir buvo paskelbti 1995 m. gegužės mėn. žurnale „Annals of Mathematics“.
Nuo to momento praėjo daug laiko, tačiau visuomenėje vis dar gaji nuomonė, kad paskutinė Ferma teorema yra neišsprendžiama. Tačiau net ir tie, kurie žino apie rastą įrodymą, ir toliau dirba šia kryptimi – nedaugelis yra patenkinti, kad Didžioji teorema reikalauja 130 puslapių sprendimo!
Todėl dabar daugelio matematikų (dažniausiai mėgėjų, o ne mokslininkų profesionalų) pastangos metamos paprasto ir glausto įrodymo paieškoms, tačiau šis kelias, greičiausiai, niekur nenuves...
šaltinis
Paskutinė Fermato teorema Singhas Simonas
"Ar paskutinė Ferma teorema buvo įrodyta?"
Tai buvo tik pirmas žingsnis siekiant įrodyti Taniyama-Shimura spėjimą, tačiau Wileso strategija buvo puikus matematinis proveržis, o rezultatas nusipelnė būti paskelbtas. Tačiau dėl Wileso prisiekusio tylėjimo jis negalėjo papasakoti visam pasauliui apie savo rezultatą ir neįsivaizdavo, kas dar galėtų padaryti tokį pat reikšmingą proveržį.
Wilesas prisimena savo filosofinį požiūrį į bet kurį potencialų varžovą: „Niekas nenori praleisti metų ką nors įrodydamas ir atrasti, kad kažkas kitas sugebėjo rasti įrodymą keliomis savaitėmis anksčiau. Tačiau, kaip bebūtų keista, kadangi bandžiau išspręsti problemą, kuri iš esmės buvo laikoma neišsprendžiama, varžovų nelabai bijojau. Tiesiog nesitikėjau, kad aš ar kas nors kitas sugalvos idėją, kuri atves į įrodymą.
1988 m. kovo 8 d. Wilesas buvo sukrėstas, kai pirmuosiuose laikraščių puslapiuose išvydo antraštes dideliais šriftais: „Paskutinė Fermato teorema įrodyta“. „The Washington Post“ ir „New York Times“ pranešė, kad trisdešimt aštuonerių metų Yoichi Miyaoka iš Tokijo Metropoliteno universiteto išsprendė sunkiausią pasaulyje matematikos problemą. Miyaoka dar nepaskelbė savo įrodymo, bet apibūdino jo pažangą seminare Maxo Plancko matematikos institute Bonoje. Miyaokos kalboje dalyvavęs Donas Tsagiras matematikų bendruomenės optimizmą išreiškė tokiais žodžiais: „Miyaokos pateiktas įrodymas yra nepaprastai įdomus, o kai kurie matematikai mano, kad jis turi didelę tikimybę, kad jis bus teisingas. Dar nesame visiškai tikri, bet kol kas įrodymai atrodo labai džiuginantys.
Kalbėdamas seminare Bonoje, Miyaoka papasakojo apie savo požiūrį į problemos sprendimą, kurį jis svarstė visiškai kitu, algebriniu-geometriniu požiūriu. Per pastaruosius dešimtmečius geometrai giliai ir subtiliai suprato matematinius objektus, ypač paviršių savybes. Aštuntajame dešimtmetyje rusų matematikas S. Arakelovas bandė nustatyti paraleles tarp algebrinės geometrijos ir skaičių teorijos uždavinių. Tai buvo viena iš Langlandso programos krypčių, ir matematikai tikėjosi, kad neišspręstas skaičių teorijos problemas galima išspręsti tiriant atitinkamas geometrijos problemas, kurios taip pat liko neišspręstos. Ši programa buvo žinoma kaip paralelizmo filosofija. Tie algebriniai geometrai, kurie bandė išspręsti uždavinius skaičių teorijoje, buvo vadinami „aritmetiniais algebriniais geometrijais“. 1983 m. jie paskelbė savo pirmąją reikšmingą pergalę, kai Gerdas Faltingsas iš Prinstono pažangiųjų studijų instituto reikšmingai prisidėjo prie Ferma teoremos supratimo. Prisiminkite, kad, pasak Fermat, lygtis
adresu n didesnis nei 2 neturi sveikųjų skaičių sprendinių. Faltingsas nusprendė, kad jis padarė pažangą įrodydamas paskutinę Ferma teoremą, tyrinėdamas geometrinius paviršius, susijusius su skirtingomis reikšmėmis n. Paviršiai, susiję su Fermato lygtimis įvairioms reikšmėms n, skiriasi viena nuo kitos, bet turi vieną bendrą savybę – visos turi kiaurymes, arba, paprasčiau tariant, skylutes. Šie paviršiai yra keturmačiai, kaip ir modulinių formų grafikai. Dviejų paviršių dvimačiai pjūviai parodyti fig. 23. Paviršiai, susiję su Fermato lygtimi, atrodo panašiai. Kuo didesnė vertė n lygtyje, tuo daugiau skylių yra atitinkamame paviršiuje.

Ryžiai. 23. Šie du paviršiai gauti naudojant kompiuterinę programą Mathematica. Kiekvienas iš jų žymi lygtį tenkinančių taškų lokusą x n + y n = z n(kairėje esančiam paviršiui n=3, paviršiui dešinėje n=5). Kintamieji x Ir yčia laikomi sudėtingais
Faltingsas sugebėjo įrodyti, kad kadangi tokie paviršiai visada turi keletą skylių, susijusi Fermato lygtis gali turėti tik baigtinį sveikųjų skaičių sprendinių rinkinį. Sprendimų skaičius gali būti bet koks – nuo nulio, kaip manė Fermat, iki milijono ar milijardo. Taigi, Faltingsas neįrodė paskutinės Ferma teoremos, bet bent jau sugebėjo atmesti galimybę, kad Ferma lygtis turi be galo daug sprendinių.
Po penkerių metų Miyaoka pranešė, kad žengė dar vieną žingsnį toliau. Tada jam buvo vos dvidešimt. Miyaoka suformulavo hipotezę dėl tam tikros nelygybės. Tapo aišku, kad įrodyti jo geometrinę spėjimą reikš įrodyti, kad Ferma lygties sprendinių skaičius yra ne tik baigtinis, bet lygus nuliui. Miyaokos požiūris buvo panašus į Wileso požiūrį, nes jie abu bandė įrodyti paskutinę Ferma teoremą, susiedami ją su pagrindine hipoteze kitoje matematikos šakoje. Miyaokai tai buvo algebrinė geometrija; Wilesui kelias į įrodymą ėjo per elipsines kreives ir modulines formas. Dideliam Wileso apmaudui, jis vis dar stengėsi įrodyti Taniyama-Shimura spėjimą, kai Miyaoka tvirtino, kad turi visišką savo spėliojimo, taigi ir Ferma paskutinės teoremos, įrodymą.
Praėjus dviem savaitėms po kalbos Bonoje, Miyaoka paskelbė penkis puslapius skaičiavimų, kurie sudarė jo įrodymo esmę, ir prasidėjo nuodugnus tyrimas. Skaičių teoretikai ir algebrinės geometrijos specialistai visame pasaulyje studijavo eilutę po eilutės, skelbė skaičiavimus. Po kelių dienų matematikai atrado vieną įrodymo prieštaravimą, kuris nekėlė nerimo. Viena Miyaokos darbo dalis paskatino skaičių teorijos teiginį, kuris, išverstas į algebrinės geometrijos kalbą, pateikė teiginį, prieštaraujantį kelerius metus anksčiau gautam rezultatui. Nors tai nebūtinai panaikino visą Miyaokos įrodymą, atrastas prieštaravimas netilpo į skaičių teorijos ir geometrijos paralelizmo filosofiją.
Dar po dviejų savaičių Gerdas Faltingsas, nutiesęs kelią Miyaokei, paskelbė atradęs tikslią akivaizdaus paralelizmo pažeidimo priežastį – samprotavimo spragą. Japonų matematikas buvo geometras ir nebuvo visiškai griežtas, perkeldamas savo idėjas į mažiau pažįstamą skaičių teorijos sritį. Skaičių teoretikų armija įnirtingai stengėsi užkamšyti spragą Miyaokos įrodyme, bet veltui. Praėjus dviem mėnesiams po to, kai Miyaoka pareiškė, kad turi visišką paskutinės Ferma teoremos įrodymą, matematikų bendruomenė padarė vieningą išvadą: Miyaokos įrodymas buvo pasmerktas žlugti.
Kaip ir ankstesnių nesėkmingų įrodymų atveju, Miyaoka sugebėjo gauti daug įdomių rezultatų. Kai kurie jo įrodymo fragmentai buvo verti dėmesio kaip labai išradingi geometrijos pritaikymai skaičių teorijai, o vėlesniais metais kiti matematikai jas naudojo kai kurioms teoremoms įrodyti, tačiau niekam nepavyko tokiu būdu įrodyti Paskutinės Ferma teoremos.
Furoras dėl paskutinės Ferma teoremos greitai nutilo, o laikraščiuose pasirodė trumpi pranešimai, kad trijų šimtų metų senumo galvosūkis vis dar liko neišspręstas. Ant Niujorko Aštuntosios gatvės metro stoties sienos pasirodė toks užrašas, kurį, be jokios abejonės, įkvėpė paskutinė Ferma teorema spaudoje: „Eq. xn + yn = zn neturi sprendimų. Radau tikrai nuostabų šio fakto įrodymą, bet negaliu jo čia užrašyti, nes atvažiavo mano traukinys.
Iš knygos Johnas Lennonas autorius Goldmanas Albertas63 skyrius Senojo Maklennono ūkis, praėjus maždaug pusantro mėnesio po grįžimo į Niujorką, vieną lapkričio vakarą Lennonų bute suskambo telefonas. Yoko atsiliepė telefonu. Vyriškas balsas su puertorikietišku akcentu paklausė Yoko Ono. Apsimetinėja
Iš knygos „Akvariumo istorija“. Fleitininko knyga autorius Romanovas Andrejus Igorevičius Iš knygos Paskutinė Ferma teorema pateikė Singhas SimonasFermato problema 1963 m., kai jam buvo tik dešimt metų, Andrew Wilesas jau susižavėjo matematika. „Mokykloje mėgau spręsti problemas, parsinešdavau jas namo ir iš kiekvienos problemos kurdavau vis naujas. Tačiau geriausia problema, su kuria aš kada nors susidūriau, buvo vietiniame
Iš knygos Nikita Chruščiovas. Reformatorius autorius Chruščiovas Sergejus NikitichasNuo Pitagoro teoremos iki paskutinės Ferma teoremos Pitagoro teorema ir begalinis Pitagoro trigubų skaičius buvo aptarti knygoje E.T. Bello „Didžioji problema“ – ta pati bibliotekos knyga, kuri patraukė Andrew Wileso dėmesį. Ir nors pitagoriečiai pasiekė beveik visiškai
Iš knygos „Mirties arba geležinio filatelisto išbandymas“. autorius Arbatova Marija IvanovnaMatematika po paskutinės Ferma teoremos įrodymo Kaip bebūtų keista, pats Wilesas dėl savo pranešimo jautė prieštaringus jausmus: „Proga kalbai parinkta labai gerai, tačiau pati paskaita man sukėlė prieštaringus jausmus. Darbas su įrodymu
Iš knygos Vienas gyvenimas, du pasauliai autorius Aleksejeva Nina IvanovnaŪkis ar sodyba? 1958 m. vasario 13 d. visi centriniai Maskvos ir tuometiniai regioniniai laikraščiai paskelbė Ukrainos komunistų partijos centrinio komiteto sprendimą „Dėl klaidos perkant karves iš Zaporožės srities kolūkiečių“. Kalbėjome net ne apie visą regioną, o apie du jo rajonus: Primorsky
Iš knygos „Žvaigždės“ ir šiek tiek nervingai autorius Žolkovskis Aleksandras KonstantinovičiusDešimtas skyrius KROKODILŲ ŪKIS Jie važiavo vaizdingu keliu senu Jono automobiliu, sėdėdami galinėse sėdynėse. Prie vairo sėdėjo juodas vairuotojas ryškiais marškiniais ir keistai nukirsta galva. Ant jo nuskustos kaukolės stovėjo vielos kietų juodų plaukų krūmai, logiška
Iš knygos Mano akimis autorius Adelgeimas PavelasTolstojaus nendrių ūkis Kirilas nuvyko į Tolstojaus fondo biurą susitikti su rusais. Grįžęs pasakė, kad Aleksandra Lvovna Tolstaja buvo pasibaisėjusi, ir pasakė: „Jūs negalite likti viešbutyje, tai labai pavojinga jums ir jūsų vaikams.“ Tą pačią dieną
Iš knygos „Gyvūnų pasaulyje“ [2 leidimas] autorius Drozdovas Nikolajus NikolajevičiusPontriagino teorema Tuo pat metu kaip konservatorijoje mano tėvas studijavo Maskvos valstybiniame universitete, studijavo mechaniką ir matematiką. Studijas baigė sėkmingai ir net kurį laiką dvejojo, rinkdamasis profesiją. Muzikologija laimėjo, nes pasinaudojo jo matematine mąstysena. Vienas iš mano tėvo klasiokų
Iš knygos Sunki siela: literatūrinis dienoraštis. Atsiminimų straipsniai. Eilėraščiai autorius Zlobinas Vladimiras AnanevičiusTeorema Teoremą apie religinės asociacijos teisę pasirinkti kunigą reikia įrodyti. Ji skamba taip: „Stačiatikių bendruomenė kuriama... dvasingai vadovaujant bendruomenės išrinktam kunigui, kuris gavo vyskupijos vyskupo palaiminimą“.
Iš knygos „Sapno atmintis“ [Eilėraščiai ir vertimai] autorius Puchkova Elena OlegovnaOžkų ūkis Vasarą kaime daug darbų. Kai lankėmės Khomutets kaime, ten buvo pjaunamas šienas ir kvepiančios bangelės nuo ką tik nupjautų žolelių tarsi persmelkė viską aplink.Vaistažoles reikia nupjauti laiku, kad jos nepernoktų, tada viskas, kas vertinga ir maistinga, išliks. juose. Tai
Iš knygos Wormy Apple [My Life with Steve Jobs] autorius Brennan ChrisannI. Ūkis („Čia, iš vištų išmatų...“) Štai iš vištų išmatų Vienas išsigelbėjimas – šluota. Meilė – kuri? - Ji nuvedė mane į vištidę. Pešiodamos grūdus, vištos kaukiasi, gaidžiai svarbiai žingsniuoja. Ir be dydžio ir cenzūros Eilėraščiai kuriami mintyse. Apie Provanso popietę
Iš knygos Mano kelionės. Kiti 10 metų autorius Konyukhovas Fiodoras FilippovičiusVasaros ūkis Šiaudas, kaip rankinis žaibas, stiklas į žolę; Kitas, pasirašęs ant tvoros, arklio lovyje įžiebė žalios vandens stiklinės laužą. Į mėlyną prieblandą Devynios antys klaidžioja, siūbuodami, palei provėžą lygiagrečių linijų dvasia. Čia višta į nieką žiūri viena
Iš autorės knygosSugriautas ūkis Rami saulė kaip tamsiai raudona gėlė, Nugrimzdo į žemę, į saulėlydį įaugdama, Bet nakties uždanga dykinėjančioje galioje Nutraukė pasaulį, sutrikdytą žvilgsnio. Be stogo fermoje viešpatavo tyla, Lyg kas jai plaukus būtų nuplėšęs, Jie kovojo dėl kaktuso
Iš autorės knygos9 skyrius Vienas ūkis Laura Schueler ir aš nusprendėme švęsti vidurinės mokyklos pabaigą leisdamos į trijų savaičių kelionę. Nelabai supratome, ką mums reiškia mokyklos baigimas, bet žinojome, kad šį įvykį reikia švęsti. Taigi aptarėme, ką darysime
Iš autorės knygosPasiruošimas lenktynėms. Aliaska, Linda Pletner Iditarod Farm yra kasmetinės kinkinių šunų lenktynės Aliaskoje. Maršruto ilgis – 1150 mylių (1800 km). Tai ilgiausios pasaulyje šunų rogių lenktynės. Startas (iškilmingas) – 2000 m. kovo 4 d. iš Ankoridžo. Pradėti
Pierre'as Fermatas, skaitydamas Diofanto Aleksandriečio „Aritmetiką“ ir apmąstydamas jos problemas, turėjo įprotį savo apmąstymų rezultatus užrašyti trumpų komentarų forma knygos paraštėse. Prieš aštuntąją Diofanto problemą knygos paraštėse Fermatas rašė: Priešingai, neįmanoma išskaidyti nei kubo į du kubus, nei bikvadrato į du bikvadratus, ir apskritai jokios galios, didesnės už kvadratą, į dvi laipsnius su tuo pačiu rodikliu. Atradau tikrai nuostabų to įrodymą, bet šie laukai tam per siauri» / E.T. Bellas „Matematikos kūrėjai“. M., 1979, p.69/. Atkreipiu jūsų dėmesį į elementarų Fermato teoremos įrodymą, kurį gali suprasti bet kuris matematika besidomintis gimnazistas.
Palyginkime Ferma komentarą apie Diofanto problemą su šiuolaikine paskutinės Ferma teoremos formuluote, kuri turi lygties formą.
« Lygtis
x n + y n = z n(kur n yra sveikasis skaičius, didesnis už du)
neturi teigiamų sveikųjų skaičių sprendinių»
Komentaras yra logiškai susijęs su užduotimi, panašus į loginį predikato ryšį su dalyku. Tai, ką tvirtina Diofanto problema, priešingai, tvirtina Ferma komentaras.
Fermato komentarą galima interpretuoti taip: jei kvadratinė lygtis su trimis nežinomaisiais turi begalinį sprendinių skaičių visų Pitagoro skaičių tripletų aibėje, tai, priešingai, lygtis su trimis nežinomaisiais, kurių laipsnis yra didesnis už kvadratą.
Lygtyje apie jos ryšį su Diofanto problema nėra net užuominos. Jo teiginys reikalauja įrodymo, tačiau nėra sąlygos, iš kurios būtų galima daryti išvadą, kad jis neturi teigiamų sveikųjų skaičių sprendinių.
Man žinomos lygties įrodymo parinktys susiveda į tokį algoritmą.
- Jos išvada laikoma Ferma teoremos lygtis, kurios pagrįstumas patikrinamas įrodymais.
- Ta pati lygtis vadinama originalus lygtis, iš kurios turi vykti jos įrodymas.
Dėl to susiformavo tautologija: „ Jei lygtis neturi sprendinių teigiamais sveikaisiais skaičiais, tada ji neturi sprendinių teigiamais sveikaisiais skaičiais„Tautoologijos įrodymas yra akivaizdžiai neteisingas ir neturi jokios prasmės. Tačiau tai įrodo prieštaravimas.
- Daroma prielaida, kuri yra priešinga tam, kas nurodyta lygtyje, kurią reikia įrodyti. Tai neturėtų prieštarauti pradinei lygčiai, bet taip yra. Nėra prasmės įrodinėti tai, kas priimta be įrodymų, ir priimti be įrodymų tai, ką reikia įrodyti.
- Remiantis priimta prielaida, atliekami absoliučiai teisingi matematiniai veiksmai ir veiksmai, siekiant įrodyti, kad ji prieštarauja pradinei lygčiai ir yra klaidinga.
Todėl jau 370 metų Ferma paskutinės teoremos lygties įrodymas tebėra neįgyvendinama specialistų ir matematikos entuziastų svajonė.
Teoremos išvadą priėmiau lygtį, o aštuntą Diofanto uždavinį ir jos lygtį – kaip teoremos sąlygą.
„Jei lygtis x 2 + y 2 = z 2
(1) turi begalinį sprendinių skaičių visų Pitagoro skaičių trigubų aibėje, tada, atvirkščiai, lygtis x n + y n = z n
, Kur n > 2
(2) neturi teigiamų sveikųjų skaičių aibės sprendinių.
Įrodymas.
A) Visi žino, kad (1) lygtis turi begalinį sprendinių skaičių visų Pitagoro skaičių trigubų aibėje. Įrodykime, kad nė vienas Pitagoro skaičių trigubas, kuris yra (1) lygties sprendimas, nėra (2) lygties sprendimas.
Remdamiesi lygybės grįžtamumo dėsniu, sukeičiame (1) lygties puses. Pitagoro skaičiai (z, x, y) gali būti interpretuojami kaip stačiojo trikampio kraštinių ilgiai ir kvadratai (x 2, y 2, z 2) gali būti interpretuojamas kaip kvadratų, pastatytų ant jo hipotenuzės ir kojų, plotas.
Padauginkime lygties (1) kvadratų plotus iš savavališko aukščio h :
z 2 h = x 2 h + y 2 h (3)
(3) lygtis gali būti aiškinama kaip gretasienio tūrio lygybė dviejų gretasienių tūrių sumai.
Tegul trijų gretasienių aukštis h = z :
z 3 = x 2 z + y 2 z (4)
Kubo tūris suskaidomas į du tūrius iš dviejų gretasienių. Kubo tūrį paliksime nepakeistą, o pirmojo gretasienio aukštį sumažinsime iki x ir sumažinkite antrojo gretasienio aukštį iki y . Kubo tūris yra didesnis už dviejų kubų tūrių sumą:
z 3 > x 3 + y 3 (5)
Ant Pitagoro skaičių trigubų rinkinio ( x, y, z ) adresu n=3 (2) lygties sprendinių negali būti. Vadinasi, visų Pitagoro skaičių trigubų aibėje kubo neįmanoma išskaidyti į du kubus.
Įveskime (3) lygtį trijų gretasienių aukštį h = z 2 :
z 2 z 2 = x 2 z 2 + y 2 z 2 (6)
Lygiagretainio vamzdžio tūris išskaidomas į dviejų gretasienių tūrių sumą.
Kairiąją (6) lygties pusę paliekame nepakeistą. Jo dešinėje pusėje aukštis z 2
sumažinti iki X
pirmoje kadencijoje ir prieš tai 2 val
antroje kadencijoje.
(6) lygtis virto nelygybe:
Gretasienio tūris skaidomas į du dviejų gretasienių tūrius.
Kairiąją (8) lygties pusę paliekame nepakeistą.
Dešinėje pusėje aukštis zn-2
sumažinti iki xn-2
pirmoje kadencijoje ir sumažinti iki y n-2
antroje kadencijoje. (8) lygtis tampa nelygybe:
| z n > x n + y n | (9) |
Pitagoro skaičių tripletų aibėje negali būti vieno (2) lygties sprendinio.
Vadinasi, visų Pitagoro skaičių trigubų aibėje visiems n > 2 (2) lygtis neturi sprendinių.
Buvo gautas „tikrai stebuklingas įrodymas“, bet tik trynukams Pitagoro skaičiai. Tai yra įrodymų trūkumas ir P. Fermato atsisakymo iš jo priežastis.
B)Įrodykime, kad (2) lygtis neturi sprendinių ne Pitagoro skaičių tripletų aibėje, kuri reiškia savavališko Pitagoro skaičių trigubo šeimą. z = 13, x = 12, y = 5 ir savavališko teigiamų sveikųjų skaičių trigubo šeima z = 21, x = 19, y = 16
Abu skaičių trynukai yra savo šeimos nariai:
| (13, 12, 12); (13, 12,11);…; (13, 12, 5) ;…; (13,7, 1);…; (13,1, 1) | (10) | |
| (21, 20, 20); (21, 20, 19);…;(21, 19, 16);…;(21, 1, 1) | (11) |
Šeimos narių skaičius (10) ir (11) yra lygus pusei sandaugos iš 13 iš 12 ir 21 iš 20, ty 78 ir 210.
Kiekvienas šeimos narys (10) turi z = 13 ir kintamieji X Ir adresu 13 > x > 0 , 13 > y > 0 1
Kiekvienas šeimos narys (11) turi z = 21 ir kintamieji X Ir adresu , kurių reikšmės yra sveikieji skaičiai 21 > x > 0 , 21 > y > 0 . Kintamieji iš eilės mažėja 1 .
Sekos (10) ir (11) skaičių trigubai gali būti pavaizduoti kaip trečiojo laipsnio nelygybių seka:
| 13 3 < 12 3 + 12 3 ;13 3 < 12 3 + 11 3 ;…; 13 3 < 12 3 + 8 3 ; 13 3 > 12 3 + 7 3 ;…; 13 3 > 1 3 + 1 3 | ||
| 21 3 < 20 3 + 20 3 ; 21 3 < 20 3 + 19 3 ; …; 21 3 < 19 3 + 14 3 ; 21 3 > 19 3 + 13 3 ;…; 21 3 > 1 3 + 1 3 |
ir ketvirtojo laipsnio nelygybių pavidalu:
| 13 4 < 12 4 + 12 4 ;…; 13 4 < 12 4 + 10 4 ; 13 4 > 12 4 + 9 4 ;…; 13 4 > 1 4 + 1 4 | ||
| 21 4 < 20 4 + 20 4 ; 21 4 < 20 4 + 19 4 ; …; 21 4 < 19 4 + 16 4 ;…; 21 4 > 1 4 + 1 4 |
Kiekvienos nelygybės teisingumas patikrinamas pakeliant skaičius į trečią ir ketvirtą laipsnius.
Didesnio skaičiaus kubas negali būti išskaidytas į du mažesnių skaičių kubus. Ji yra mažesnė arba didesnė už dviejų mažesnių skaičių kubelių sumą.
Didesnio skaičiaus bikvadratas negali būti išskaidytas į du mažesnių skaičių bikvadratus. Jis yra arba mažesnis, arba didesnis už mažesnių skaičių dvigubų kvadratų sumą.
Didėjant eksponentui, visos nelygybės, išskyrus kairiąją kraštutinę nelygybę, turi tą pačią reikšmę:
Visi jie turi tą pačią reikšmę: didesnio skaičiaus laipsnis yra didesnis nei dviejų mažesnių skaičių, turinčių tą patį rodiklį, laipsnių sumą:
| 13 n > 12 n + 12 n ; 13 n > 12 n + 11 n ;…; 13 n > 7 n + 4 n ;…; 13 n > 1 n + 1 n | (12) | |
| 21 n > 20 n + 20 n ; 21 n > 20 n + 19 n ;…; ;…; 21 n > 1 n + 1 n | (13) |
Kairysis kraštutinis sekų (12) (13) narys reiškia silpniausią nelygybę. Jo teisingumas lemia visų vėlesnių sekos (12) nelygybių teisingumą n > 8 ir seka (13) ties n > 14 .
Tarp jų negali būti lygybės. Savavališkas teigiamų sveikųjų skaičių trigubas (21, 19, 16) nėra paskutinės Ferma teoremos (2) lygties sprendimas. Jei savavališkas teigiamų sveikųjų skaičių trigubas nėra lygties sprendimas, tai lygtis neturi sprendinių teigiamų sveikųjų skaičių aibėje, ką reikia įrodyti.
SU) Ferma komentaras apie Diofanto problemą teigia, kad neįmanoma suskaidyti. apskritai nėra laipsnio, didesnio už kvadratą, dvi laipsniai su tuo pačiu rodikliu».
Bučinys laipsnis, didesnis už kvadratą, iš tikrųjų negali būti išskaidytas į du laipsnius su tuo pačiu rodikliu. Jokių bučinių laipsnį, didesnį už kvadratą, galima išskaidyti į dvi laipsnius su tuo pačiu laipsniu.
Bet koks savavališkas teigiamų sveikųjų skaičių trigubas (z, x, y) gali priklausyti šeimai, kurios kiekvienas narys susideda iš pastovaus skaičiaus z ir dviem skaičiais mažesni z . Kiekvienas šeimos narys gali būti pavaizduotas nelygybės forma, o visos susidariusios nelygybės gali būti pavaizduotos nelygybių sekos forma:
| z n< (z — 1) n + (z — 1) n ; z n < (z — 1) n + (z — 2) n ; …; z n >1 n + 1 n | (14) |
Nelygybių seka (14) prasideda nelygybėmis, kurių kairioji pusė yra mažesnė už dešinę, ir baigiasi nelygybėmis, kurių dešinioji pusė yra mažesnė už kairę. Didėjant rodikliui n > 2 nelygybių skaičius dešinėje sekos (14) pusėje didėja. Su eksponentu n = k visos nelygybės kairėje sekos pusėje pakeičia savo reikšmę ir įgauna nelygybių, esančių dešinėje sekos nelygybių (14) pusėje, reikšmę. Padidinus visų nelygybių eksponentą, kairioji pusė pasirodo didesnė nei dešinė:
| z k > (z-1) k + (z-1) k ; z k > (z-1) k + (z-2) k ;…; z k > 2 k + 1 k ; z k > 1 k + 1 k | (15) |
Toliau didėjant rodikliui n>k nė viena iš nelygybių nekeičia savo reikšmės ir nevirsta lygybe. Tuo remiantis galima teigti, kad bet kuris savavališkai pasirinktas teigiamų sveikųjų skaičių trigubas (z, x, y) adresu n > 2 , z > x , z > y
Savavališkai pasirinktame teigiamų sveikųjų skaičių triguba z gali būti savavališkai didelis natūralusis skaičius. Visiems natūraliems skaičiams, kurie nėra didesni už z , Paskutinė Ferma teorema įrodyta.
D) Kad ir koks didelis skaičius z , natūralioje skaičių eilutėje prieš ją yra didelė, bet baigtinė sveikųjų skaičių aibė, o po jos – begalinė sveikųjų skaičių aibė.
Įrodykime, kad visa begalinė natūraliųjų skaičių aibė yra didelė z , sudaro skaičių trigubus, kurie nėra paskutinės Ferma teoremos lygties sprendiniai, pavyzdžiui, savavališkas teigiamų sveikųjų skaičių trigubas (z + 1, x ,y) , kuriame z + 1 > x Ir z + 1 > y visoms eksponento reikšmėms n > 2 nėra paskutinės Ferma teoremos lygties sprendimas.
Atsitiktinai parinktas teigiamų sveikųjų skaičių trigubas (z + 1, x, y) gali priklausyti skaičių trigubų šeimai, kurios kiekvienas narys susideda iš pastovaus skaičiaus z+1 ir du skaičiai X Ir adresu , įgaunant skirtingas vertybes, mažesnius z+1 . Šeimos nariai gali būti pavaizduoti kaip nelygybė, kai pastovi kairioji pusė yra mažesnė arba didesnė už dešinę. Nelygybės gali būti išdėstytos nelygybių sekos forma:
Toliau didėjant rodikliui n>k iki begalybės, nė viena iš sekos (17) nelygybių nekeičia savo reikšmės ir nevirsta lygybe. Eilėje (16) nelygybė susidarė iš savavališkai pasirinkto teigiamų sveikųjų skaičių trigubo (z + 1, x, y) , gali būti dešinėje formos pusėje (z + 1) n > x n + y n arba būti kairėje formos pusėje (z+1)n< x n + y n .
Bet kokiu atveju, teigiamų sveikųjų skaičių trigubas (z + 1, x, y) adresu n > 2 , z + 1 > x , z + 1 > y sekoje (16) reiškia nelygybę ir negali atstovauti lygybės, tai yra, ji negali pateikti paskutinės Ferma teoremos lygties sprendimo.
Lengva ir paprasta suprasti galios nelygybių sekos kilmę (16), kurioje paskutinė nelygybė kairėje ir pirmoji nelygybė dešinėje yra priešingos reikšmės nelygybės. Priešingai, moksleiviams, gimnazistams ir aukštųjų mokyklų studentams nėra lengva ir sunku suprasti, kaip iš nelygybių sekos (17) susidaro nelygybių seka (16), kurioje visos nelygybės turi tą pačią reikšmę. .
Iš eilės (16), padidinus sveikąjį nelygybių laipsnį 1 vienetu, paskutinė kairėje pusėje esanti nelygybė paverčiama pirmąja priešingos prasmės nelygybe dešinėje. Taigi nelygybių skaičius kairėje sekos pusėje mažėja, o nelygybių skaičius dešinėje didėja. Tarp paskutinės ir pirmosios priešingos reikšmės galios nelygybės būtinai yra galios lygybė. Jo laipsnis negali būti sveikasis skaičius, nes tik nesveikieji skaičiai yra tarp dviejų iš eilės einančių natūraliųjų skaičių. Ne sveikojo skaičiaus laipsnio laipsnio lygybė pagal teoremos sąlygas negali būti laikoma (1) lygties sprendiniu.
Jei seka (16) toliau didinsime laipsnį 1 vienetu, tai paskutinė jos kairės pusės nelygybė pavirs į pirmąja dešinės pusės priešingos reikšmės nelygybe. Dėl to neliks kairiosios nelygybės kairėje ir liks tik dešinės pusės nelygybės, kurios bus didėjančių galios nelygybių seka (17). Tolesnis jų sveikojo skaičiaus galios padidinimas 1 vienetu tik sustiprina jo galios nelygybes ir kategoriškai atmeta sveikojo skaičiaus galios lygybės galimybę.
Vadinasi, apskritai joks laipsnio nelygybių (17) sekos natūraliojo skaičiaus (z+1) sveikasis laipsnis negali būti išskaidomas į dvi sveikąsias laipsnes su tuo pačiu eksponentu. Todėl (1) lygtis neturi begalinės natūraliųjų skaičių aibės sprendinių, ką reikėjo įrodyti.
Vadinasi, paskutinė Ferma teorema įrodyta visa:
- A dalyje) visiems trynukams (z, x, y) Pitagoro skaičiai (Fermato atradimas yra tikrai puikus įrodymas),
- B skirsnyje visiems bet kurio trejeto šeimos nariams (z, x, y) Pitagoro skaičiai,
- C dalyje) visiems skaičių trigubams (z, x, y) , nėra dideli skaičiai z
- D dalyje) visiems skaičių trigubams (z, x, y) natūralių skaičių serija.
|
Pakeitimai padaryti 2010-09-05 |
Kurias teoremas galima ir kurios negali įrodyti prieštaravimu?
Aiškinamasis matematinių terminų žodynas apibrėžia įrodymą prieštaraudamas teoremai, priešingai nei atvirkštinei teoremai.
„Įrodymas prieštaravimu yra teoremos (teiginio) įrodinėjimo metodas, kurio metu įrodoma ne pati teorema, o jos ekvivalentinė (ekvivalentinė) teorema. Įrodymas prieštaravimu naudojamas visada, kai sunku įrodyti tiesioginę teoremą, o priešingą teoremą įrodyti lengviau. Įrodinėjant prieštaravimu teoremos išvada pakeičiama jos neigimu, o per samprotavimus pasiekiamas sąlygų neigimas, t.y. į prieštaravimą, į priešingą (priešingai tam, kas duota; ši redukcija į absurdą įrodo teoremą).
Matematikoje labai dažnai naudojamas įrodinėjimas prieštaravimu. Įrodinėjimas prieštaravimu grindžiamas neįtraukiamo vidurio dėsniu, kuris susideda iš to, kad iš dviejų teiginių (teiginių) A ir A (A neigimas), vienas iš jų yra teisingas, o kitas yra klaidingas./Aiškinamasis matematikos terminų žodynas: vadovas mokytojams/O. V. Manturovas [ir kt.]; Redaguota V. A. Ditkina.- M.: Išsilavinimas, 1965.- 539 p.: iliustr.-C.112/.
Nebūtų geriau atvirai deklaruoti, kad įrodinėjimo prieštaravimu metodas nėra matematinis metodas, nors jis naudojamas matematikoje, kad tai yra loginis metodas ir priklauso logikai. Ar priimtina sakyti, kad įrodinėjimas prieštaravimu „naudojamas, kai tiesioginę teoremą sunku įrodyti“, nors iš tikrųjų jis naudojamas tada ir tik tada, kai nėra pakaitalo.
Ypatingo dėmesio nusipelno tiesioginės ir atvirkštinės teoremų santykio viena su kita apibūdinimas. „Atvirkštinė teorema duotai teoremai (arba duotai teoremai) yra teorema, kurioje sąlyga yra išvada, o išvada yra duotosios teoremos sąlyga. Ši teorema atvirkštinės teoremos atžvilgiu vadinama tiesiogine teorema (originalu). Tuo pačiu metu atvirkštinė teorema į atvirkštinę teoremą bus duota teorema; todėl tiesioginė ir atvirkštinė teoremos vadinamos tarpusavyje atvirkštinėmis. Jei tiesioginė (duota) teorema yra teisinga, tai atvirkštinė teorema ne visada teisinga. Pavyzdžiui, jei keturkampis yra rombas, tai jo įstrižainės yra viena kitai statmenos (tiesioginė teorema). Jei keturkampyje įstrižainės yra viena kitai statmenos, tai keturkampis yra rombas - tai klaidinga, ty atvirkštinė teorema yra klaidinga./Aiškinamasis matematikos terminų žodynas: vadovas mokytojams/O. V. Manturovas [ir kt.]; Redaguota V. A. Ditkina.- M.: Išsilavinimas, 1965.- 539 p.: iliustr.-C.261 /.
Ši tiesioginės ir atvirkštinės teoremos ryšio charakteristika neatsižvelgia į tai, kad tiesioginės teoremos sąlyga priimama kaip duota, be įrodymo, todėl jos teisingumas negarantuojamas. Atvirkštinės teoremos sąlyga nepriimama kaip duota, nes tai yra įrodytos tiesioginės teoremos išvada. Jos teisingumą patvirtina tiesioginės teoremos įrodymas. Šis esminis loginis tiesioginės ir atvirkštinės teoremų sąlygų skirtumas pasirodo esąs lemiamas sprendžiant, kurias teoremas galima ir kurios negali būti įrodinėjamos loginiu metodu prieštaraujant.
Tarkime, kad galvoje yra tiesioginė teorema, kurią galima įrodyti įprastu matematiniu metodu, tačiau tai yra sudėtinga. Suformuluokime jį bendrai ir trumpai taip: iš A turėtų E . Simbolis A turi pateiktos teoremos sąlygos reikšmę, priimtą be įrodymo. Simbolis E svarbi yra teoremos išvada, kurią reikia įrodyti.
Tiesioginę teoremą įrodysime prieštaravimu, logiška metodas. Teoremai, kuri turi, įrodyti naudojamas loginis metodas ne matematinis būklė ir logiška sąlyga. Jį galima gauti, jei teoremos matematinė sąlyga iš A turėtų E , papildyti visiškai priešinga sąlyga iš A nedaryk to E .
Rezultatas buvo logiška prieštaringa naujosios teoremos sąlyga, kurią sudaro dvi dalys: iš A turėtų E Ir iš A nedaryk to E . Gauta naujosios teoremos sąlyga atitinka loginį neįtraukiamo vidurio dėsnį ir atitinka teoremos įrodymą prieštaravimu.
Pagal įstatymą viena prieštaringos sąlygos dalis yra klaidinga, kita dalis yra teisinga, o trečioji – pašalinama. Įrodinėjimas prieštaravimu turi užduotį ir tikslą tiksliai nustatyti, kuri iš dviejų teoremos sąlygos dalių yra klaidinga. Nustačius klaidingą sąlygos dalį, nustatoma, kad kita dalis yra tikra, o trečioji neįtraukiama.
Pagal aiškinamąjį matematikos terminų žodyną, „Įrodymas – samprotavimai, kurių metu nustatomas bet kurio teiginio (nuosprendžio, teiginio, teoremos) teisingumas ar klaidingumas“. Įrodymas prieštaravimu yra samprotavimas, kurio metu nustatoma melas(absurdiškumas) išvados, kylančios iš klaidingaįrodinėjamos teoremos sąlygos.
Duota: iš A turėtų E ir iš A nedaryk to E .
Įrodykite: iš A turėtų E .
Įrodymas: Teoremos loginėje sąlygoje yra prieštaravimas, kurį reikia išspręsti. Sąlygos prieštaravimas turi rasti savo sprendimą įrodyme ir jo rezultate. Nepriekaištingai ir be klaidų motyvuojant rezultatas pasirodo klaidingas. Klaidingos išvados logiškai teisingu samprotavimu priežastis gali būti tik prieštaringa sąlyga: iš A turėtų E Ir iš A nedaryk to E .
Nėra jokių abejonių, kad viena sąlygos dalis yra klaidinga, o kita šiuo atveju yra teisinga. Abi sąlygos dalys turi tą pačią kilmę, yra priimamos kaip duomenys, prielaidos, vienodai galimos, vienodai leistinos ir pan. Loginio samprotavimo metu nebuvo aptikta nei vieno loginio požymio, kuris skirtų vieną sąlygos dalį nuo kitos . Todėl tokiu pat mastu tai gali būti iš A turėtų E ir galbūt iš A nedaryk to E . pareiškimas iš A turėtų E Gal būt klaidinga, tada pareiškimas iš A nedaryk to E bus tiesa. pareiškimas iš A nedaryk to E gali būti klaidingas, tada teiginys iš A turėtų E bus tiesa.
Vadinasi, tiesioginės teoremos neįmanoma įrodyti prieštaravimu.
Dabar tą pačią tiesioginę teoremą įrodysime įprastu matematiniu metodu.
Duota: A .
Įrodykite: iš A turėtų E .
Įrodymas.
1. Iš A turėtų B
2. Iš B turėtų IN (pagal anksčiau įrodytą teoremą)).
3. Iš IN turėtų G (pagal anksčiau įrodytą teoremą).
4. Iš G turėtų D (pagal anksčiau įrodytą teoremą).
5. Iš D turėtų E (pagal anksčiau įrodytą teoremą).
Remiantis tranzityvumo dėsniu, iš A turėtų E . Tiesioginė teorema įrodoma įprastu metodu.
Tegul įrodyta tiesioginė teorema turi teisingą atvirkštinę teoremą: iš E turėtų A .
Įrodykime tai įprastai matematinės metodas. Atvirkštinės teoremos įrodymas gali būti išreikštas simboline forma kaip matematinių operacijų algoritmas.
Duota: E
Įrodykite: iš E turėtų A .
Įrodymas.
1. Iš E turėtų D
2. Iš D turėtų G (pagal anksčiau įrodytą atvirkštinę teoremą).
3. Iš G turėtų IN (pagal anksčiau įrodytą atvirkštinę teoremą).
4. Iš IN nedaryk to B (atvirkštinė teorema nėra teisinga). Štai kodėl iš B nedaryk to A .
Šioje situacijoje nėra prasmės tęsti atvirkštinės teoremos matematinį įrodymą. Situacijos priežastis logiška. Neteisinga atvirkštinė teorema negali būti pakeista niekuo. Todėl neįmanoma įrodyti šios atvirkštinės teoremos įprastu matematiniu metodu. Visa viltis yra įrodyti šią atvirkštinę teoremą prieštaravimu.
Norint tai įrodyti prieštaravimu, reikia pakeisti jo matematinę sąlygą logiška prieštaringa sąlyga, kuri savo prasme susideda iš dviejų dalių – klaidinga ir teisinga.
Atvirkštinė teorema teigia: iš E nedaryk to A . Jos būklė E , iš kurios daroma išvada A , yra tiesioginės teoremos įrodinėjimo įprastu matematiniu metodu rezultatas. Ši sąlyga turi būti išsaugota ir papildyta pareiškimu iš E turėtų A . Dėl papildymo gauname prieštaringą naujosios atvirkštinės teoremos sąlygą: iš E turėtų A Ir iš E nedaryk to A . Remiantis tuo logiškai prieštaringa sąlyga, atvirkštinė teorema gali būti įrodyta naudojant teisingą logiška tik samprotavimas ir tik logiška metodas prieštaringai. Įrodinėjant prieštaravimu, bet kokie matematiniai veiksmai ir operacijos yra pavaldūs loginiams ir todėl neįskaitomi.
Pirmoje prieštaringo teiginio dalyje iš E turėtų A sąlyga E buvo įrodyta tiesioginės teoremos įrodymu. Antroje dalyje iš E nedaryk to A sąlyga E buvo manoma ir priimta be įrodymų. Vienas iš jų yra klaidingas, o kitas - tiesa. Turite įrodyti, kuris iš jų yra klaidingas.
Mes tai įrodome teisingai logiška samprotavimus ir atrasti, kad jo rezultatas yra klaidinga, absurdiška išvada. Klaidingos loginės išvados priežastis yra prieštaringa loginė teoremos sąlyga, kurią sudaro dvi dalys – klaidinga ir teisinga. Klaidinga dalis gali būti tik teiginys iš E nedaryk to A , kuriame E buvo priimtas be įrodymų. Tuo jis skiriasi nuo E pareiškimus iš E turėtų A , o tai įrodo tiesioginės teoremos įrodymas.
Taigi teiginys yra teisingas: iš E turėtų A , ką ir reikėjo įrodyti.
Išvada: loginiu metodu prieštaravimu įrodoma tik atvirkštinė teorema, kuri turi tiesioginę matematiniu metodu įrodytą teoremą ir kurios negalima įrodyti matematiniu metodu.
Gauta išvada įgyja išskirtinę reikšmę įrodinėjimo metodo atžvilgiu, prieštaraudama Didžiajai Ferma teoremai. Didžioji dauguma bandymų tai įrodyti remiasi ne įprastu matematiniu metodu, o loginiu įrodinėjimo prieštaravimu būdu. Wileso paskutinės Ferma teoremos įrodymas nėra išimtis.
Dmitrijus Abrovas straipsnyje „Fermato teorema: Wileso įrodymų fenomenas“ paskelbė komentarą apie Wileso paskutinės Ferma teoremos įrodymą. Pasak Abrarovo, Wilesas įrodo paskutinę Ferma teoremą pasitelkęs nuostabų vokiečių matematiko Gerhardo Frey (g. 1944 m.) atradimą, kuris susiejo galimą Ferma lygties sprendimą. x n + y n = z n
, Kur n > 2
, su kita, visiškai kitokia lygtimi. Šią naują lygtį pateikia speciali kreivė (vadinama Frey's elipsine kreive). Frey kreivė pateikiama labai paprasta lygtimi:
.
„Frey lygino kiekvieną sprendimą (a, b, c) Fermato lygtis, tai yra skaičiai, tenkinantys ryšį a n + b n = c n, aukščiau pateikta kreivė. Tokiu atveju sektų paskutinė Ferma teorema.(Citata iš: Abrarov D. „Fermato teorema: Wileso įrodymų fenomenas“)
Kitaip tariant, Gerhardas Frey pasiūlė Ferma paskutinės teoremos lygtį x n + y n = z n
, Kur n > 2
, turi sprendinius teigiamais sveikaisiais skaičiais. Tie patys sprendimai, remiantis Frey'io prielaida, yra jo lygties sprendimai
y 2 + x (x - a n) (y + b n) = 0
, kurią suteikia elipsinė kreivė.
Andrew Wilesas priėmė šį nuostabų Frey atradimą ir su jo pagalba matematinės metodas įrodė, kad šio radinio, tai yra Frey elipsinės kreivės, nėra. Todėl nėra lygties ir jos sprendinių, pateiktų neegzistuojančia elipsine kreive, todėl Wilesas turėjo priimti išvadą, kad nėra paskutinės Ferma teoremos ir pačios Ferma teoremos lygties. Tačiau jis sutinka su kuklesne išvada, kad paskutinės Ferma teoremos lygtis neturi sprendinių teigiamais sveikaisiais skaičiais.
Nenuginčijamas faktas gali būti tas, kad Wilesas priėmė prielaidą, kuri savo prasme yra visiškai priešinga tam, kas išdėstyta didžiojoje Ferma teoremoje. Ji įpareigoja Wilesą prieštaravimu įrodyti paskutinę Ferma teoremą. Sekime jo pavyzdžiu ir pažiūrėkime, kas iš šio pavyzdžio išeis.
Paskutinė Ferma teorema teigia, kad lygtis x n + y n = z n , Kur n > 2 , neturi teigiamų sveikųjų skaičių sprendinių.
Pagal loginį įrodinėjimo prieštaravimu metodą šis teiginys išlaikomas, priimamas kaip pateiktas be įrodymo, o vėliau papildomas priešingu teiginiu: lygtimi. x n + y n = z n , Kur n > 2 , turi sprendinius teigiamais sveikaisiais skaičiais.
Preziumuojamas pareiškimas taip pat priimamas kaip pateiktas, be įrodymų. Abu teiginiai, nagrinėjant pagrindinių logikos dėsnių požiūriu, vienodai galiojantys, vienodai galiojantys ir vienodai galimi. Per teisingą samprotavimą būtina nustatyti, kuris teiginys yra klaidingas, kad būtų galima nustatyti, ar kitas teiginys yra teisingas.
Teisingas samprotavimas baigiasi klaidinga, absurdiška išvada, kurios logiška priežastis gali būti tik prieštaringa įrodomos teoremos sąlyga, kurioje yra dvi tiesiogiai priešingos reikšmės dalys. Jie buvo logiška absurdiškos išvados priežastis, įrodinėjimo prieštaravimu rezultatas.
Tačiau logiškai teisingo samprotavimo metu nebuvo aptiktas nė vienas požymis, pagal kurį būtų galima nustatyti, kuris teiginys yra klaidingas. Tai gali būti teiginys: lygtis x n + y n = z n , Kur n > 2 , turi sprendinius teigiamais sveikaisiais skaičiais. Tuo pačiu pagrindu tai galėtų būti toks teiginys: lygtis x n + y n = z n , Kur n > 2 , neturi teigiamų sveikųjų skaičių sprendinių.
Dėl samprotavimo galima padaryti tik vieną išvadą: Paskutinė Ferma teorema negali būti įrodyta prieštaravimu.
Būtų visai kas kita, jei paskutinė Ferma teorema būtų atvirkštinė teorema, kurios tiesioginė teorema įrodyta įprastu matematiniu metodu. Šiuo atveju tai galėtų būti įrodyta prieštaravimu. Ir kadangi tai yra tiesioginė teorema, jos įrodymas turėtų būti pagrįstas ne loginiu įrodinėjimo prieštaravimu metodu, o įprastu matematiniu metodu.
Anot D. Abrarov, garsiausias šiuolaikinis Rusijos matematikas akademikas V. I. Arnoldas į Wileso įrodymą reagavo „aktyviai skeptiškai“. Akademikas pareiškė: „tai nėra tikroji matematika – tikroji matematika yra geometrinė ir turi stiprių sąsajų su fizika.“ (Citata iš: Abrarov D. „Fermato teorema: Wileso įrodymų fenomenas“. Akademiko teiginys išreiškia pačią esmę). Wiles'o nematematinis paskutinės Ferma teoremos įrodymas.
Priešingai, neįmanoma įrodyti nei to, kad paskutinės Ferma teoremos lygtis neturi sprendinių, nei kad ji turi sprendinių. Wileso klaida yra ne matematinė, o loginė – įrodymo panaudojimas prieštaravimu ten, kur jo vartojimas neturi prasmės ir neįrodo didžioji Ferma teorema.
Paskutinė Ferma teorema negali būti įrodyta net naudojant įprastą matematinį metodą, jei ji pateikia: lygtį x n + y n = z n , Kur n > 2 , neturi teigiamų sveikųjų skaičių sprendinių, o jei norite jame įrodyti: lygtį x n + y n = z n , Kur n > 2 , neturi teigiamų sveikųjų skaičių sprendinių. Šioje formoje yra ne teorema, o tautologija, neturinti prasmės.
Pastaba. Mano BTF įrodymas buvo aptartas viename iš forumų. Vienas iš Trotilo dalyvių, skaičių teorijos ekspertas, padarė tokį autoritetingą pareiškimą pavadinimu: „Trumpas atpasakojimas apie tai, ką padarė Mirgorodskis“. Cituoju pažodžiui:
« A. Jis įrodė, kad jei z 2 = x 2 + y , Tai z n > x n + y n . Tai gerai žinomas ir gana akivaizdus faktas.
IN. Jis paėmė du trigubus - pitagorietišką ir nepitagorišką ir paprasta paieška parodė, kad konkrečiai, konkrečiai triviečių šeimai (78 ir 210 vnt.) BTF tenkina (ir tik už tai).
SU. Ir tada autorius nutylėjo faktą, kad nuo < vėliau gali pasirodyti = , ne tik > . Paprastas kontrpavyzdys – perėjimas n=1 V n=2 Pitagoro triguboje.
D. Šis punktas nieko reikšmingo neprisideda prie BTF įrodymo. Išvada: BTF neįrodyta.
Apsvarstysiu jo išvadą punktas po punkto.
A. Tai įrodo visos begalinės Pitagoro skaičių trigubų rinkinio BTF. Įrodyta geometriniu metodu, kurį, kaip tikiu, atradau ne aš, o atradau iš naujo. Ir jį atrado, kaip tikiu, pats P. Fermatas. Fermatas galėjo tai turėti omenyje, kai rašė:
„Atradau tikrai nuostabų to įrodymą, bet šios sritys tam per siauros. Ši mano prielaida grindžiama tuo, kad Diofanto uždavinyje, prieš kurį Fermatas rašė knygos paraštėse, mes kalbame apie Diofanto lygties sprendimus, kurie yra Pitagoro skaičių tripletai.
Begalinė Pitagoro skaičių tripletų aibė yra Diofato lygties sprendiniai, o Ferma teoremoje, priešingai, nė vienas iš sprendinių negali būti Ferma teoremos lygties sprendimas. Ir tikrai nuostabus Fermato įrodymas yra tiesiogiai susijęs su šiuo faktu. Fermatas vėliau galėjo išplėsti savo teoremą į visų natūraliųjų skaičių aibę. Visų natūraliųjų skaičių aibėje BTF nepriklauso „išskirtinai gražių teoremų rinkiniui“. Tai mano prielaida, kurios negalima nei įrodyti, nei paneigti. Jis gali būti priimtas arba atmestas.
IN.Šiuo metu įrodau, kad tiek savavališkai paimto Pitagoro skaičių trigubo šeima, tiek savavališkai paimto ne Pitagoro trigubo BTF skaičių šeima yra patenkinta. Tai būtina, bet nepakankama ir tarpinė nuoroda mano BTF įrodyme. . Mano pateikti pavyzdžiai apie Pitagoro skaičių trigubą šeimą ir ne Pitagoro skaičių trigubą šeimą turi konkrečių pavyzdžių, kurie suponuoja ir neatmeta kitų panašių pavyzdžių, reikšmę.
Trotilo teiginys, kad aš „paprasta paieška įrodžiau, kad konkrečiai, konkrečiai trynukų šeimai (78 ir 210 vnt.) BTF tenkina (ir tik už tai), yra nepagrįstas. Jis negali paneigti fakto, kad aš lygiai taip pat galiu imtis kitų pitagoriečių ir ne pitagoriečių trigubų pavyzdžių, kad gaučiau konkrečią apibrėžtą vieno ir kito trigubų šeimą.
Kad ir kokią trynukų porą imčiau, patikrinti jų tinkamumą problemai išspręsti, mano nuomone, galima atlikti tik „paprasto surašymo“ metodu. Kito metodo nežinau ir man jo nereikia. Jei Trotilui tai nepatiko, jis turėjo pasiūlyti kitą metodą, kurio jis nedaro. Nieko nesiūlant mainais, neteisinga smerkti „paprastą pertekliškumą“, kuris šiuo atveju yra nepakeičiamas.
SU. Aš praleidau = tarp< и < на основании того, что в доказательстве БТФ рассматривается уравнение z 2 = x 2 + y (1), kuriame laipsnis n > 2 — visas teigiamas skaičius. Iš lygybės tarp nelygybių išplaukia privalomas 1 lygties svarstymas jei laipsnio reikšmė nėra sveikoji n > 2 . Trotilas, skaičiuoja privalomas svarstymas apie lygybę tarp nelygybių iš tikrųjų mano būtina BTF įrodyme, nagrinėjant (1) lygtį su ne visa laipsnio vertė n > 2 . Aš tai padariau sau ir radau lygtį (1) su ne visa laipsnio vertė n > 2 turi trijų skaičių sprendinį: z, (z-1), (z-1) ne sveikajam rodikliui.
1Ivlievas Yu.A.
Straipsnis skirtas esminės matematinės klaidos, padarytos įrodant paskutinę Ferma teoremą XX amžiaus pabaigoje, aprašymui. Aptikta klaida ne tik iškreipia tikrąją teoremos prasmę, bet ir trukdo plėtoti naują aksiomatinį skaičių laipsnių ir natūralių skaičių eilučių tyrimo metodą.
1995 metais buvo paskelbtas straipsnis, panašaus dydžio į knygą, kuriame pranešama apie garsiosios Ferma (paskutinės) teoremos (WTF) įrodymą (teoremos istoriją ir bandymus ją įrodyti žr., pvz. ). Po šio įvykio pasirodė daug mokslinių straipsnių ir mokslo populiarinimo knygų, propaguojančių šį įrodymą, tačiau nė vienas iš šių darbų neatskleidė esminės matematinės klaidos, kuri įsivėlė net ne dėl autoriaus kaltės, o dėl kažkokio keisto optimizmo, apėmusio jį. mintyse matematikai, tyrę šią problemą ir susijusias problemas. Psichologiniai šio reiškinio aspektai buvo ištirti. Pateikiame išsamią įvykusios klaidos analizę, kuri nėra privataus pobūdžio, o yra neteisingo sveikųjų skaičių laipsnių savybių supratimo pasekmė. Kaip parodyta, Fermato problema kyla iš naujo aksiomatinio požiūrio į šių savybių tyrimą, kuris dar nebuvo pritaikytas šiuolaikiniame moksle. Tačiau jam kelią stojo klaidingas įrodymas, pateikęs skaičių teorijos specialistams klaidingas gaires ir nukreipęs Ferma problemos tyrėjus nuo tiesioginio ir adekvačios jos sprendimo. Šis darbas skirtas pašalinti šią kliūtį.
1. WTF įrodymo metu padarytos klaidos anatomija
Labai ilgo ir varginančio samprotavimo procese pradinis Fermato teiginys buvo performuluotas lyginant p-ojo laipsnio diofantinę lygtį su 3 eilės elipsinėmis kreivėmis (žr. 0,4 ir 0,5 colio teoremas). Šis palyginimas privertė praktiškai kolektyvinio įrodymo autorius paskelbti, kad jų metodas ir samprotavimai veda prie galutinio Ferma problemos sprendimo (prisiminkime, kad WTF neturėjo pripažintų įrodymų savavališkų sveikųjų skaičių laipsniams iki praėjusio amžiaus 90-ųjų. amžiuje). Šio svarstymo tikslas – nustatyti matematinį aukščiau pateikto palyginimo neteisingumą ir, atlikus analizę, rasti esminę klaidą pateiktame įrodyme.
a) Kur ir kokia klaida?
Taigi, seksime tekstą, kur 448 p. sakoma, kad po G. Frey „šmaikštaus sumanymo“ atsivėrė galimybė įrodyti WTF. 1984 metais G. Frey pasiūlė ir
K. Ribetas vėliau įrodė, kad tariama elipsinė kreivė, vaizduojanti Ferma lygties hipotetinį sveikąjį skaičių
y 2 = x(x + u p)(x - v p) (1)
negali būti modulinis. Tačiau A. Wilesas ir R. Tayloras įrodė, kad kiekviena pusiau skaičiuojama elipsinė kreivė, apibrėžta racionaliųjų skaičių srityje, yra modulinė. Tai leido daryti išvadą apie Ferma lygties sveikųjų skaičių sprendinių neįmanomumą, taigi ir apie Ferma teiginio, kuris A. Wileso užrašyme buvo parašytas kaip 0.5 teorema: tebūnie lygybė, pagrįstumą.
u p+ v p+ w p = 0 (2)
Kur tu, v, w- racionalieji skaičiai, sveikasis rodiklis p ≥ 3; tada (2) tenkinama tik tuo atveju, jei uvw = 0 .
Dabar, matyt, turėtume grįžti atgal ir kritiškai pagalvoti, kodėl kreivė (1) a priori buvo suvokiama kaip elipsė ir koks jos tikrasis ryšys su Fermato lygtimi. Numatydamas šį klausimą, A. Wilesas remiasi Y. Hellegouarcho darbu, kuriame jis rado būdą susieti Ferma lygtį (manoma, išspręsta sveikaisiais skaičiais) su hipotetine trečios eilės kreive. Skirtingai nei G. Frey, I. Elleguarche nesiejo savo kreivės su modulinėmis formomis, tačiau jo (1) lygties gavimo metodas buvo panaudotas A. Wileso įrodymui toliau tobulinti.
Pažvelkime į darbą atidžiau. Autorius savo samprotavimus atlieka projekcinės geometrijos požiūriu. Supaprastinus kai kuriuos jos žymėjimus ir suderinus juos su , matome, kad Abelio kreivė
Y 2 = X(X - β p) (X + γ p) (3)
lyginama Diofanto lygtis
x p+ y p+ z p = 0 (4)
Kur x, y, z yra nežinomi sveikieji skaičiai, p yra sveikasis rodiklis iš (2), o Diofanto lygties (4) sprendiniai α p , β p , γ p naudojami Abelio kreivei (3) parašyti.
Dabar, norint įsitikinti, kad tai yra 3 eilės elipsinė kreivė, reikia atsižvelgti į (3) kintamuosius X ir Y Euklido plokštumoje. Tam naudojame gerai žinomą elipsinių kreivių aritmetikos taisyklę: jei kubinėje algebrinėje kreivėje yra du racionalūs taškai ir tiesė, einanti per šiuos taškus, kerta šią kreivę kitame taške, tai pastarasis taip pat yra racionalus taškas. . Hipotetinė lygtis (4) formaliai parodo taškų sudėjimo tiesėje dėsnį. Jei pakeisime kintamuosius x p = A, y p = B, z p = C ir nukreipkite gautą tiesę išilgai X ašies (3), tada ji susikirs su 3 laipsnio kreive trijuose taškuose: (X = 0, Y = 0), (X = β p, Y = 0) , (X = - γ p, Y = 0), kas atsispindi Abelio kreivės (3) žymėjime ir panašiame žymėjime (1). Tačiau ar kreivė (3) arba (1) iš tikrųjų yra elipsė? Akivaizdu, kad ne, nes Euklido linijos atkarpos, sudedant joje taškus, paimamos netiesine skale.
Grįžtant prie tiesinių Euklido erdvės koordinačių sistemų, vietoj (1) ir (3) gauname formules, kurios labai skiriasi nuo elipsinių kreivių formulių. Pavyzdžiui, (1) gali būti tokios formos:
η 2p = ξ p (ξ p + u p)(ξ p - v p) (5)
kur ξ p = x, η p = y, o kreipimasis į (1) šiuo atveju norint gauti WTF atrodo neteisėtas. Nepaisant to, kad (1) atitinka kai kuriuos elipsinių kreivių klasės kriterijus, jis netenkina svarbiausio kriterijaus būti 3 laipsnio lygtimi tiesinėje koordinačių sistemoje.
b) Klaidų klasifikavimas
Taigi, dar kartą grįžkime į svarstymo pradžią ir pažiūrėkime, kaip daroma išvada apie WTF tiesą. Pirma, daroma prielaida, kad yra koks nors Fermato lygties sprendimas teigiamais sveikaisiais skaičiais. Antra, šis sprendimas savavališkai įterpiamas į žinomos formos algebrinę formą (3 laipsnio plokštumos kreivė), darant prielaidą, kad taip gautos elipsės kreivės egzistuoja (antroji nepatvirtinta prielaida). Trečia, kadangi kiti metodai įrodo, kad tam tikra sukonstruota kreivė yra nemodulinė, tai reiškia, kad jos nėra. Tai leidžia daryti išvadą: nėra sveikųjų Ferma lygties sprendinių, todėl WTF yra teisinga.
Šiuose argumentuose yra viena silpnoji grandis, kuri, išsamiai patikrinus, pasirodo esanti klaida. Ši klaida padaroma antrajame įrodinėjimo proceso etape, kai daroma prielaida, kad hipotetinis Ferma lygties sprendimas yra ir 3 laipsnio algebrinės lygties, apibūdinančios žinomos formos elipsinę kreivę, sprendimas. Pati savaime tokia prielaida būtų pateisinama, jei nurodyta kreivė tikrai būtų elipsė. Tačiau, kaip matyti iš punkto 1a), ši kreivė pateikiama netiesinėmis koordinatėmis, todėl ji yra „iliuzinė“, t.y. tiesinėje topologinėje erdvėje tikrai neegzistuoja.
Dabar turime aiškiai klasifikuoti rastą klaidą. Tai slypi tame, kad tai, ką reikia įrodyti, pateikiama kaip įrodymo argumentas. Klasikinėje logikoje ši klaida vadinama „užburtu ratu“. Šiuo atveju sveikasis Ferma lygties sprendimas lyginamas (matyt, vienareikšmiškai) su fiktyvia, neegzistuojančia elipsine kreive, o tada visas tolesnio samprotavimo patosas išnaudojamas įrodyti, kad gauta konkreti tokios formos elipsinė kreivė. iš hipotetinių Ferma lygties sprendinių, neegzistuoja.
Kaip atsitiko, kad tokia elementari klaida rimtame matematiniame darbe buvo praleista? Tikriausiai taip atsitiko dėl to, kad tokio tipo „iliuzinės“ geometrinės figūros matematikoje anksčiau nebuvo tiriamos. Iš tiesų, kam galėtų būti įdomus, pavyzdžiui, išgalvotas apskritimas, gautas iš Fermato lygties, pakeičiant kintamuosius x n/2 = A, y n/2 = B, z n/2 = C? Juk jos lygtis C 2 = A 2 + B 2 neturi sveikųjų skaičių x, y, z ir n ≥ 3 sprendinių. Netiesinėse koordinačių ašyse X ir Y toks apskritimas būtų apibūdintas lygtimi, labai panašia į standartinę formą:
Y 2 = - (X - A) (X + B),
kur A ir B nebėra kintamieji, o konkretūs skaičiai, nustatyti pagal aukščiau pateiktą pakeitimą. Bet jei skaičiams A ir B suteikiama jų pradinė forma, kurią sudaro jų galios pobūdis, tada dešinėje lygties pusėje esančių veiksnių žymėjimo nevienalytiškumas iškart krenta į akis. Ši savybė padeda atskirti iliuziją nuo tikrovės ir pereiti nuo netiesinių prie tiesinių koordinačių. Kita vertus, jei skaičius laikysime operatoriais, lygindami juos su kintamaisiais, kaip pavyzdžiui (1), tai abu turi būti vienarūšiai dydžiai, t.y. turi turėti tuos pačius laipsnius.
Šis skaičių, kaip operatorių, galių supratimas taip pat leidžia suprasti, kad Fermato lygties palyginimas su iliuzine elipsine kreive nėra vienareikšmis. Paimkite, pavyzdžiui, vieną iš faktorių dešinėje (5) pusėje ir išskaidykite jį į p tiesinius veiksnius, įvesdami kompleksinį skaičių r, kad r p = 1 (žr., pavyzdžiui):
ξ p + u p = (ξ + u)(ξ + r u)(ξ + r 2 u)...(ξ + r p-1 u) (6)
Tada forma (5) gali būti pavaizduota kaip išskaidymas į pirminius kompleksinių skaičių veiksnius pagal algebrinės tapatybės tipą (6), tačiau tokio skilimo unikalumas bendruoju atveju yra abejotinas, kaip kadaise parodė Kummeris. .
2. Išvados
Iš ankstesnės analizės matyti, kad vadinamoji elipsinių kreivių aritmetika negali atskleisti, kur ieškoti WTF įrodymo. Po darbo Fermato teiginys, beje, laikomas šio straipsnio epigrafu, buvo pradėtas suvokti kaip istorinis pokštas ar apgaulė. Tačiau iš tikrųjų pasirodo, kad juokavo ne Fermatas, o specialistai, 1984 metais Vokietijoje Obervolfache susirinkę į matematikos simpoziumą, kuriame G. Frey išsakė savo šmaikščią mintį. Tokio neatsargaus pareiškimo pasekmės privedė matematiką kaip visumą prie visuomenės pasitikėjimo praradimo ribos, apie kurią išsamiai aprašoma ir dėl to neišvengiamai kyla klausimas dėl mokslo institucijų atsakomybės visuomenei. Fermato lygties palyginimas su Frey kreive (1) yra viso Wileso įrodymo, susijusio su Ferma teorema, „užraktas“, ir jei nėra atitikimo tarp Fermato kreivės ir modulinių elipsinių kreivių, tada nėra jokio įrodymo.
Neseniai pasirodė įvairios interneto ataskaitos, kad kai kurie žinomi matematikai pagaliau išsiaiškino Wileso Ferma teoremos įrodymą, sugalvoję jo pagrindimą „minimalaus“ sveikųjų skaičių perskaičiavimu Euklido erdvėje. Tačiau jokios naujovės negali panaikinti klasikinių, žmonijos jau gautų matematikos rezultatų, ypač fakto, kad nors bet koks eilinis skaičius sutampa su jo kiekybiniu analogu, jis negali būti jo pakaitalas skaičių palyginimo operacijose, taigi. su neišvengiama išvada, kad Frey kreivė (1) iš pradžių nėra elipsė, t.y. ar ne pagal apibrėžimą.
BIBLIOGRAFIJA:
- Ivlievas Yu.A. Fermato paskutinės teoremos gimtojo įrodymo rekonstrukcija – Jungtinis mokslinis žurnalas (skyrius „Matematika“). 2006 m. balandis, Nr. 7 (167) p. 3-9, taip pat žr. Tarptautinės informatizacijos akademijos Praci Lugansk filialas. Ukrainos švietimo ir mokslo ministerija. Skhidnoukransky nacionalinis universitetas pavadintas. V.Dal. 2006 Nr.2 (13) p.19-25.
- Ivlievas Yu.A. Didžiausia XX amžiaus mokslinė apgaulė: paskutinės Fermato teoremos „įrodymas“ – gamtos ir inžinerijos mokslai (skyrius „Matematikos istorija ir metodika“). 2007 rugpjūčio Nr.4 (30) p.34-48.
- Edwardsas G. (Edwards H.M.) Paskutinė Ferma teorema. Genetinis įvadas į algebrinių skaičių teoriją. Per. iš anglų kalbos Redaguota B.F.Skubenko. M.: Mir 1980, 484 p.
- Hellegouarch Y. Points d´ordre 2p h sur les courbes elliptiques – Acta Arithmetica. 1975 XXVI p.253-263.
- Wiles A. Modulinės elipsės kreivės ir paskutinė Ferma teorema – Matematikos metraščiai. 1995 gegužė v.141 Antra serija Nr.3 p.443-551.
Bibliografinė nuoroda
Ivlievas Yu.A. WILLES'o KLINGAS PASKUTINĖS FERMO TEOREMOS ĮRODYMAS // Fundamentalūs tyrimai. – 2008. – Nr.3. – P. 13-16;URL: http://fundamental-research.ru/ru/article/view?id=2763 (prisijungimo data: 2019-09-25). Atkreipiame jūsų dėmesį į leidyklos „Gamtos mokslų akademija“ leidžiamus žurnalus
Prieš daugelį metų gavau laišką iš Taškento iš Valerijaus Muratovo, sprendžiant iš rašysenos, paauglystės amžiaus vyro, kuris tada gyveno Kommunisticheskaya gatvėje 31 numeriu. Vaikinas buvo ryžtingas: „Eik tiesiai į reikalą. Kiek sumokėsite man už tai, kad įrodžiau Ferma teoremą? "Džiaugiuosi bent 500 rublių. Kitu metu būčiau tau įrodęs nemokamai, bet dabar man reikia pinigų..."
Nuostabus paradoksas: mažai žmonių žino, kas yra Fermatas, kada jis gyveno ir ką veikė. Dar mažiau žmonių gali apibūdinti jo puikią teoremą net pačiais bendriausiais terminais. Tačiau visi žino, kad egzistuoja kažkokia Ferma teorema, kurios įrodymu viso pasaulio matematikai kovojo daugiau nei 300 metų, bet negali įrodyti!
Yra daug ambicingų žmonių, o pats suvokimas, kad yra kažkas, ko kiti negali padaryti, dar labiau skatina jų ambicijas. Todėl į viso pasaulio akademijas, mokslo institutus ir net laikraščių redakcijas atkeliavo ir ateina tūkstančiai (!) Didžiosios teoremos įrodymų – precedento neturintis ir niekada nesulaužytas pseudomokslinės mėgėjiškos veiklos rekordas. Yra net toks terminas: „Fermatistai“, tai yra Didžiosios teoremos įrodinėjimo apsėsti žmonės, kurie profesionalius matematikus visiškai kankino reikalavimais įvertinti savo darbą. Garsus vokiečių matematikas Edmundas Landau net parengė standartą, pagal kurį atsakė: „Jūsų Ferma teoremos įrodyme puslapyje yra klaida...“, o jo magistrantai užsirašė puslapio numerį. Ir tada 1994 m. vasarą viso pasaulio laikraščiai paskelbė kai ką visiškai sensacingo: Didžioji teorema buvo įrodyta!
Taigi, kas yra Fermatas, kokia yra problema ir ar ji tikrai išspręsta? Pierre'as Fermatas gimė 1601 m. odininko, turtingo ir gerbiamo žmogaus šeimoje – jis ėjo antruoju konsulu savo gimtajame Bomono mieste – kažkas panašaus į mero padėjėją. Pierre'as iš pradžių studijavo pas vienuolius pranciškonus, vėliau – Tulūzos teisės fakultete, kur vėliau vertėsi teise. Tačiau Fermat interesų spektras peržengė jurisprudenciją. Ypač domėjosi klasikine filologija, žinomi jo komentarai apie antikos autorių tekstus. O mano antroji aistra – matematika.
XVII amžiuje, kaip ir po daugelio metų, tokios profesijos nebuvo: matematiko. Todėl visi didieji to meto matematikai buvo matematikai „ne visą darbo dieną“: Rene Descartes tarnavo armijoje, François Viète buvo teisininkas, Francesco Cavalieri – vienuolis. Tada nebuvo jokių mokslinių žurnalų, o klasikinis mokslininkas Pierre'as Fermatas per savo gyvenimą nepaskelbė nė vieno mokslinio darbo. Buvo gana siauras ratas „mėgėjų“, kurie spręsdavo įvairias jiems įdomias problemas ir rašydavo vieni kitiems laiškus apie tai, kartais ginčydavosi (kaip Ferma ir Dekartas), bet dažniausiai likdavo bendraminčiais. Jie tapo naujosios matematikos pradininkais, briliantinių sėklų sėjomis, iš kurių pradėjo augti galingas šiuolaikinių matematinių žinių medis, įgaunantis stiprybės ir šakotis.
Taigi, Fermatas buvo tas pats „mėgėjas“. Tulūzoje, kur jis gyveno 34 metus, visi jį pažinojo, visų pirma, kaip tyrimų rūmų patarėją ir patyrusį teisininką. Būdamas 30 metų vedė, susilaukė trijų sūnų ir dviejų dukterų, kartais vykdavo į komandiruotes, o per vieną iš jų staiga mirė 63-eji. Viskas! Šio žmogaus, „Trijų muškietininkų“ amžininko, gyvenimas stebėtinai nenuobodus ir be nuotykių. Nuotykiai atėjo su jo Didžiąja teorema. Nekalbėkime apie visą Ferma matematinį paveldą, ir sunku apie tai kalbėti populiariai. Laikykitės mano žodžio: šis paveldas yra puikus ir įvairus. Teiginys, kad Didžioji teorema yra jo darbo viršūnė, yra labai prieštaringas. Tiesiog Didžiosios teoremos likimas yra stebėtinai įdomus, o didžiulis matematikos paslaptyse nesusipažinusių žmonių pasaulis visada domėjosi ne pačia teorema, o viskuo, kas ją supa...
Visos šios istorijos šaknų reikia ieškoti senovėje, kurią taip pamėgo Fermat. Maždaug III amžiuje Aleksandrijoje gyveno graikų matematikas Diofantas, originalus mokslininkas, mąstęs už dėžutės ribų ir išsakęs savo mintis už dėžutės ribų. Iš 13 jo „Aritmetikos“ tomų mus pasiekė tik 6. Kaip tik Fermatui sukako 20 metų, buvo išleistas naujas jo kūrinių vertimas. Fermatas labai domėjosi Diofantu, ir šie darbai buvo jo žinynas. Jos paraštėse Fermatas užrašė savo Didžiąją teoremą, kuri paprasčiausia šiuolaikine forma atrodo taip: lygtis Xn + Yn = Zn neturi sprendinio sveikaisiais skaičiais, jei n – didesnis nei 2. (Jei n = 2, sprendimas yra akivaizdus : 32 + 42 = 52). Ten, Diofantinio tomo paraštėse, Fermatas priduria: „Aš atradau šį tikrai nuostabų įrodymą, bet šios paraštės jam per siauros“.
Iš pirmo žvilgsnio tai paprastas dalykas, tačiau kai kiti matematikai pradėjo įrodinėti šią „paprastą“ teoremą, šimtą metų niekam nepavyko. Galiausiai didysis Leonhardas Euleris įrodė, kad n = 4, tada po 20 (!) metų - n = 3. Ir vėl darbas strigo daugeliui metų. Kita pergalė priklausė vokiečiui Peteriui Dirichlet (1805-1859) ir prancūzui Andrienui Legendre (1752-1833) – jie pripažino, kad Ferma buvo teisus n = 5. Tada tą patį padarė prancūzas Gabrielis Lamé (1795-1870). n = 7. Galiausiai praėjusio amžiaus viduryje vokietis Ernstas Kummeris (1810-1893) įrodė Didžiąją teoremą visoms n reikšmėms, mažesnėms nei 100 arba lygioms 100. Be to, jis įrodė tai naudodamas metodus, kuriuos Fermatas negalėjo žinoti, o tai dar labiau padidino Didžiosios teoremos paslapties nuojautą.
Taigi paaiškėjo, kad jie įrodė Fermato teoremą „gabalas po gabalo“, tačiau niekam nepavyko „visiškai“. Nauji bandymai įrodyti tik kiekybiškai padidino n reikšmes. Visi suprato, kad įdėjus daug darbo Didžiąją teoremą galima įrodyti savavališkai dideliam n skaičiui, tačiau Fermatas kalbėjo apie bet kokį vertė didesnė nei 2! Būtent šiame skirtume tarp „tiek, kiek tau patinka“ ir „bet koks“ buvo sutelkta visa problemos prasmė.
Tačiau reikia pažymėti, kad bandymai įrodyti Fermgo teoremą nebuvo tik tam tikras matematinis žaidimas, sprendžiantis sudėtingą rebusą. Šių įrodymų metu atsivėrė nauji matematiniai horizontai, iškilo ir buvo sprendžiamos problemos, tapusios naujomis matematinio medžio šakomis. Didysis vokiečių matematikas Davidas Hilbertas (1862–1943) nurodė Didžiąją teoremą kaip „stimuliuojančios įtakos, kurią mokslui gali turėti ypatinga ir iš pažiūros nereikšminga problema“, pavyzdį. Tas pats Kummeris, dirbdamas su Ferma teorema, pats įrodė teoremas, kurios sudarė skaičių teorijos, algebros ir funkcijų teorijos pagrindą. Taigi Didžiosios teoremos įrodinėjimas yra ne sportas, o tikras mokslas.
Praėjo laikas, o elektronika į pagalbą atėjo profesionaliems „fsrmatntsts“. Elektroninės smegenys negalėjo sugalvoti naujų metodų, tačiau jie tai padarė greitai. Maždaug devintojo dešimtmečio pradžioje Ferma teorema buvo įrodyta kompiuterio pagalba, kai n yra mažesnė arba lygi 5500. Pamažu šis skaičius išaugo iki 100 000, bet visi suprato, kad toks „kaupimas“ yra grynos technologijos reikalas, nieko neduodantis. į protą ar širdį. Jie negalėjo užimti Didžiosios teoremos tvirtovės tiesiai priešais ir pradėjo ieškoti sprendimo manevrų.
Devintojo dešimtmečio viduryje jaunas ne matematikas G. Filytingsas įrodė vadinamąjį „Mordelio spėjimą“, kuris, beje, taip pat „nepateko į rankas“ nė vienam matematikui 61 metus. Atsirado viltis, kad dabar, taip sakant, „puolant iš šono“, Ferma teorema gali būti išspręsta. Tačiau tada nieko neįvyko. 1986 metais vokiečių matematikas Gerhardas Frey'us knygoje „Essence“ pasiūlė naują įrodinėjimo metodą. Aš nesiimu to aiškinti griežtai, bet ne matematine, o universalia žmonių kalba, tai skamba maždaug taip: jei esame įsitikinę, kad kokios nors kitos teoremos įrodymas yra netiesioginis, kažkokiu būdu transformuotas Ferma teorema, vadinasi, įrodysime Didžiąją teoremą. Po metų amerikietis Kennethas Ribetas iš Berklio parodė, kad Frey buvo teisus ir iš tikrųjų vienas įrodymas gali būti sumažintas iki kito. Šiuo keliu ėjo daugybė matematikų įvairiose pasaulio šalyse. Viktoras Aleksandrovičius Kolyvanovas daug nuveikė, kad įrodytų Didžiąją teoremą. Trijų šimtų metų senumo neįveikiamos tvirtovės sienos ėmė drebėti. Matematikai suprato, kad jis ilgai neišsilaikys.
1993 m. vasarą senovės Kembridže, Izaoko Niutono matematikos mokslų institute, 75 žymiausi pasaulio matematikai susirinko aptarti savo problemų. Tarp jų buvo amerikietis profesorius Andrew Wilesas iš Prinstono universiteto, pagrindinis skaičių teorijos specialistas. Visi žinojo, kad jis daug metų studijavo Didžiąją teoremą. Wilesas pateikė tris pranešimus, o paskutiniame - 1993 m. birželio 23 d. - pačioje pabaigoje, nusisukęs nuo lentos, šypsodamasis pasakė:
- Manau, netęsiu...
Iš pradžių stojo mirtina tyla, paskui pliūptelėjo plojimai. Sėdintys salėje buvo pakankamai kvalifikuoti, kad suprastų: paskutinė Ferma teorema buvo įrodyta! Bet kuriuo atveju nė vienas iš dalyvaujančiųjų pateiktuose įrodymuose klaidų nerado. Niutono instituto direktoriaus pavaduotojas Peteris Goddardas žurnalistams sakė:
„Dauguma ekspertų nemanė, kad sužinos atsakymą iki savo gyvenimo pabaigos. Tai vienas didžiausių mūsų šimtmečio matematikos pasiekimų...
Praėjo keli mėnesiai, jokių komentarų ar paneigimų nebuvo. Tiesa, Wilesas savo įrodymo nepaskelbė, o tik išsiuntė vadinamuosius savo darbų atspaudus labai siauram savo kolegų ratui, o tai, žinoma, neleidžia matematikams komentuoti šios mokslinės sensacijos, o aš suprantu akademiką Liudviką Dmitrijevičių Faddejevą, kas pasakė:
„Galiu pasakyti, kad įvyko pojūtis, kai matau įrodymą savo akimis.
Faddejevas mano, kad Wileso pergalės tikimybė yra labai didelė.
„Pavyzdžiui, mano tėvas, žinomas skaičių teorijos specialistas, buvo įsitikinęs, kad teorema bus įrodyta, bet ne elementariomis priemonėmis“, – pridūrė jis.
Kitas mūsų akademikas Viktoras Pavlovičius Maslovas skeptiškai žiūrėjo į naujienas ir mano, kad Didžiosios teoremos įrodymas visai nėra aktuali matematinė problema. Taikomosios matematikos tarybos pirmininkas Maslovas savo moksliniais interesais yra toli nuo „fermatistų“, o kai sako, kad Didžiosios teoremos pilnas sprendimas yra tik sportinis interesas, jį galima suprasti. Tačiau drįstu pastebėti, kad aktualumo sąvoka bet kuriame moksle yra kintamas dydis. Prieš 90 metų Rutherfordui tikriausiai taip pat buvo pasakyta: „Na, gerai, na, radioaktyvaus skilimo teorija... Na ir kas? Kokia iš to nauda?..“
Didžiosios teoremos įrodinėjimo darbas matematikai jau daug davė ir galime tikėtis, kad duos daugiau.
„Tai, ką padarė Wilesas, perves matematikus į kitas sritis“, – sakė Peteris Goddardas. — Greičiau neuždaro vienos iš mąstymo krypčių, o iškelia naujus klausimus, į kuriuos reikės atsakyti...
Maskvos valstybinio universiteto profesorius Michailas Iljičius Zelikinas dabartinę situaciją man paaiškino taip:
Wileso darbe klaidų niekas nemato. Tačiau norint, kad šis darbas taptų moksliniu faktu, keli gerbiamieji matematikai turi savarankiškai pakartoti šį įrodymą ir patvirtinti jo teisingumą. Tai yra būtina sąlyga, kad matematinė visuomenė suprastų Wileso darbą...
Kiek tai užtruks?
Šį klausimą uždaviau vienam iš mūsų pagrindinių skaičių teorijos ekspertų, fizinių ir matematikos mokslų daktarui Aleksejui Nikolajevičiui Paršinui.
– Andrew Wiles'ui dar daug laiko...
Faktas yra tas, kad 1907 metų rugsėjo 13 dieną vokiečių matematikas P. Wolfskelis, kuris, skirtingai nei didžioji dauguma matematikų, buvo turtingas žmogus, paliko 100 tūkstančių markių tam, kuris per ateinančius 100 metų įrodys Didžiąją teoremą. Šimtmečio pradžioje palūkanos už testamentu paliktą sumą nukeliaudavo į garsiojo Getanghento universiteto iždą. Už šiuos pinigus pirmaujantys matematikai buvo kviečiami skaityti paskaitų ir atlikti mokslinį darbą. Tuo metu apdovanojimų komisijos pirmininku buvo jau minėtas Davidas Gilbertas. Jis tikrai nenorėjo mokėti premijos.
„Laimei, – pasakė didysis matematikas, – atrodo, kad neturime matematiko, išskyrus mane, kuris galėtų atlikti šią užduotį, bet aš niekada nedrįsiu nužudyti žąsies, kuri mums deda auksinius kiaušinius.
Liko keli metai iki 2007 m. termino, kurį nurodė Wolfskehl, ir, man atrodo, „Hilberto vištai“ tyko rimtas pavojus. Bet tai tikrai ne apie premiją. Tai mąstymo smalsumo ir žmogaus atkaklumo reikalas. Jie kovojo daugiau nei tris šimtus metų, bet vis tiek tai įrodė!
Ir toliau. Man įdomiausia visoje šioje istorijoje: kaip pats Fermatas įrodė savo Didžiąją teoremą? Juk visi šiandieniniai matematiniai triukai jam buvo nežinomi. Ir ar jis iš viso tai įrodė? Juk yra versija, kad jis lyg ir įrodė, bet pats rado klaidą, todėl įrodymo kitiems matematikams nesiuntė, o įrašą Diofanto tomo paraštėse pamiršo perbraukti. Todėl man atrodo, kad Didžiosios teoremos įrodymas akivaizdžiai įvyko, bet Ferma teoremos paslaptis išlieka, ir vargu ar ją kada nors atskleisime...
Galbūt tada Fermatas klydo, bet neklydo, kai rašė: „Galbūt palikuonys bus man dėkingi už tai, kad parodžiau jiems, kad senoliai ne viską žinojo, ir tai gali prasiskverbti į sąmonę tų, kurie ateina paskui mane praeiti deglas savo sūnums...“