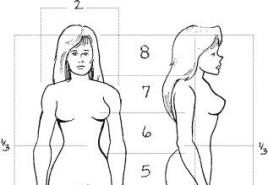
Tgx ձևի հավասարումը: Աղեղային տանգենս և աղեղային կոտանգենտ

Ալիքների հավասարումը, մասնակի դիֆերենցիալ հավասարումը, որը նկարագրում է որոշակի միջավայրում անկարգությունների տարածման գործընթացը A. N. Tikhonov and A. A. Samarskii, Equations of Mathematical Physics, 3rd ed., Moscow, 1977. - p. 155 ....

Հիպերբոլական մասնակի դիֆերենցիալ հավասարումների դասակարգում

Heatերմահաղորդման հավասարումը պարաբոլիկ տիպի մասնակի դիֆերենցիալ հավասարություն է, որը նկարագրում է շարունակական միջավայրում ջերմության տարածման գործընթացը (գազ ...

Հերթերի համակարգերի տեսության մեջ օգտագործվող մաթեմատիկական մեթոդներ

Համակարգի վիճակների հավանականությունը կարելի է գտնել Կոլմոգորովի դիֆերենցիալ հավասարումների համակարգից, որոնք կազմված են հետևյալ կանոնի համաձայն. Նրանցից յուրաքանչյուրի ձախ կողմում կա I- րդ պետության հավանականության ածանցյալ ...

Riccati- ի ոչ սկզբնական հավասարումը

(1) Ռիկատիի ընդհանուր հավասարումը ունի ձևը., (1.1), որտեղ P, Q, R- ը x- ի շարունակական ֆունկցիաներ են, քանի որ միջակայքում x փոփոխությունները Բեռնուլի ...

Տրանսպորտային փորձերի գիտական \u200b\u200bհետազոտությունների և պլանավորման հիմունքները

Մենք ստանում ենք ֆունկցիոնալ կախվածություն Y \u003d f (X) (ռեգրեսիայի հավասարություն) ՝ օգտագործելով նվազագույն քառակուսիների (OLS) մեթոդը: Որպես մոտավոր գործառույթներ օգտագործեք գծային (Y \u003d a0 + a1X) և քառակուսային կախվածություններ (Y \u003d a0 + a1X + a2X2): Օգտագործելով նվազագույն քառակուսիների մեթոդը, a0 արժեքները ...

Մենք տեղադրում ենք բևեռային կոորդինատային համակարգի բևեռը ուղղանկյուն կոորդինատային համակարգի սկզբնամասում, բևեռային առանցքը համատեղելի է դրական abscissa semiaxis- ի հետ (նկ. 3): Նկար: 3 Եկեք վերցնենք ուղիղ գծի հավասարումը նորմալ տեսքով. (3.1) - ուղղահայաց երկարությունը ...

Բևեռային կոորդինատային համակարգը ինքնաթիռում

Եկեք գրենք հավասարություն բևեռով անցնող շրջանի բևեռային կոորդինատներում `բևեռային առանցքի և շառավղի կենտրոնի վրա: OAA- ի ուղղանկյուն եռանկյունուց ստանում ենք OA \u003d OA (նկ. 4) ...

Ընտրովի տեսության հասկացություններ: Բաշխման շարք: Կորելացիայի և ռեգրեսիայի վերլուծություն

Ուսումնասիրություն. Ա) զույգ գծային ռեգրեսիայի հասկացություն. բ) նորմալ հավասարումների համակարգ կազմելը. գ) նվազագույն քառակուսիների գնահատման հատկությունները. դ) գծային ռեգրեսիայի հավասարումը գտնելու մեթոդ: Ենթադրենք ...

Դիֆերենցիալ հավասարումների լուծումների կառուցում էլեկտրաէներգիայի շարքի տեսքով

Որպես կառուցված տեսության կիրառման օրինակ ՝ դիտարկենք Բեսելի հավասարումը. (6.1) Որտեղ: Z \u003d 0 եզակի կետը կանոնավոր է: Ինքնաթիռի վերջնական մասում այլ առանձնահատկություններ չկան: (6.1) հավասարում, հետեւաբար, կառավարման հավասարումը ունի ձև, այսինքն ...

Մատրիցային հավասարումների լուծում

ХА \u003d В մատրիցայի հավասարումը կարող է լուծվել նաև երկու եղանակով. 1. Հակադարձ մատրիցը հաշվարկվում է հայտնի մեթոդներից որևէ մեկի միջոցով: Այդ դեպքում մատրիցայի հավասարության լուծումը կունենա ձևը. 2 ...

Մատրիցային հավասարումների լուծում

Վերը նկարագրված մեթոդները հարմար չեն AX \u003d XB, AX + XB \u003d C ձևի հավասարումների լուծման համար: Դրանք նույնպես հարմար չեն այն հավասարումների լուծման համար, որոնցում անհայտ X մատրիցի գործոններից գոնե մեկը դեգեներացված մատրիցա է ...

Մատրիցային հավասարումների լուծում

AX \u003d XA ձևի հավասարումները լուծվում են այնպես, ինչպես նախորդ դեպքում, այսինքն ՝ տարր առ տարր: Այստեղ լուծումը գալիս է փոխարինման մատրիցան գտնելուն: Եկեք ավելի սերտ նայենք մի օրինակի: Օրինակ. Գտեք բոլոր մատրիցները ...

Ադամանդի ուրվագծով հերթի ցանցի ստացիոնար գործարկում

Պետությունից այն կարող է գնալ հետևյալ վիճակներից որևէ մեկի. - առաջին հանգույցի հերթում հարցումն ինտենսիվությամբ ստանալու պատճառով - դրանում մշակված պահանջի առաջին հանգույցից ստացված ստացման պատճառով երրորդ հանգույցի հերթում `ինտենսիվությամբ ժամը ...

Եռանկյունաչափական գործառույթներ

Թվի արխանգանտն այն թիվ է, որի սինուսը հավասար է a- ին `եթե և: Հավասարության բոլոր արմատները կարելի է գտնել բանաձևով. ...

Մաթեմատիկական խնդիրների լուծման թվային մեթոդներ

\u003e\u003e Կամարի տանգենս և աղեղային կոտանգենտ: Tgx \u003d a, ctgx \u003d a հավասարումների լուծում

§ 19. Կամարի տանգենս և աղեղային կոտանգենտ: Tgx \u003d a, ctgx \u003d a հավասարումների լուծում

§16 օրինակում 2 մենք չկարողացանք լուծել երեք հավասարումներ.

Մենք արդեն լուծել ենք դրանցից երկուսը. Առաջինը 17 ֆունտով և երկրորդը 18 ֆունտով, դրա համար մենք պետք է ներկայացնեինք հասկացությունները արկոզին և աղեղնաձիգ: Դիտարկենք x \u003d 2 երրորդ հավասարումը:
Y \u003d tg x և y \u003d 2 գործառույթների գծապատկերներն անսահման շատ ընդհանուր կետեր ունեն, այս բոլոր կետերի abscissas- ն ունեն ձև ՝ y \u003d 2 ուղիղ գծի հատման կետի abscissa ՝ tangentoid- ի հիմնական ճյուղի հետ y \u003d 2 ուղիղ գծի հատման կետի abscissa (նկ. 90): X1 թվի համար մաթեմատիկոսները եկել են arctg 2 նշագրմանը (կարդա «երկուսի արխիվ»): Այդ դեպքում x \u003d 2 հավասարման բոլոր արմատները կարելի է նկարագրել x \u003d arctg 2 + nk բանաձևով:
Ի՞նչ է arctg 2-ը: Սա թիվ է տանգենտ որը հավասար է 2-ի, և որը պատկանում է ընդմիջմանը
Այժմ դիտարկենք tg x \u003d -2 հավասարումը:
Ֆունկցիայի գծապատկերներ ունեն անսահման շատ ընդհանուր կետեր, այս բոլոր կետերի abscissas- ն ունի ձև y \u003d -2 ուղիղ գծի խաչմերուկի կետի abscissa ՝ տանգենտոիդի հիմնական ճյուղի հետ: Համար x 2 մաթեմատիկոսները եկել են arctg (-2) նշագրմանը: Այդ դեպքում x \u003d -2 հավասարման բոլոր արմատները կարելի է նկարագրել բանաձևով

Ի՞նչ է arctg (-2): Դա թիվ է, որի շոշափումը -2 է, և որը պատկանում է ընդմիջմանը: Ուշադրություն դարձրեք (տե՛ս նկ. 90). X 2 \u003d -x 2: Սա նշանակում է, որ arctg (-2) \u003d - arctg 2:
Եկեք ձեւակերպենք արխանգանտի ընդհանուր սահմանումը:

Սահմանում 1. arctg a (arctangent a) - մի թիվ է այն ընդմիջումից, որի տանգենսը հավասար է a- ի: Այսպիսով,

Այժմ մենք կարող ենք լուծման վերաբերյալ ընդհանուր եզրակացություն անել հավասարումներ x \u003d a. x \u003d a հավասարումը լուծումներ ունի

Վերևում նշեցինք, որ arctg (-2) \u003d -agstg 2. Ընդհանրապես, a- ի ցանկացած արժեքի համար հետևյալ բանաձևը վավեր է

Օրինակ 1. Հաշվել

Օրինակ 2. Լուծել հավասարումներ.

Ա) Եկեք կազմենք լուծման բանաձև.

Այս դեպքում մենք չենք կարող հաշվարկել արքանգանտի արժեքը, ուստի հավասարման լուծումը կթողնենք ստացված տեսքով:
Պատասխան.
Օրինակ 3. Լուծել անհավասարությունները.
Դիտումների անհավասարությունը կարելի է լուծել գրաֆիկորեն ՝ հետևելով հետևյալ ծրագրերին
1) կառուցել tangentoid y \u003d tan x և ուղիղ y \u003d a;
2) տանգիզիոիդի հիմնական ճյուղի համար ընտրել x առանցքի միջակայք, որի վրա բավարարվում է նշված անհավասարությունը.
3) հաշվի առնելով y \u003d tg x գործառույթի պարբերականությունը, պատասխանը գրի՛ր ընդհանուր ձևով:
Եկեք կիրառենք այս ծրագիրը տրված անհավասարությունները լուծելու համար:

՝ ա) Եկեք կառուցենք y \u003d tanx և y \u003d 1. գործառույթների գծապատկերները. տանգենտոիդի հիմնական ճյուղի վրա դրանք հատվում են կետում

Մենք ընտրում ենք x առանցքի միջակայքը, որի վրա տանգենտոիդի հիմնական ճյուղը գտնվում է y \u003d 1 ուղիղ գծի տակ, սա է միջակայքը
Հաշվի առնելով y \u003d tgx ֆունկցիայի պարբերականությունը, մենք եզրակացնում ենք, որ նշված անհավասարությունը բավարարվում է ձևի ցանկացած միջակայքի վրա.

Բոլոր այդպիսի ընդմիջումների միությունը տվյալ անհավասարության ընդհանուր լուծումն է:
Պատասխանը կարելի է գրել մեկ այլ ձևով.

բ) Եկեք կառուցենք y \u003d tan x և y \u003d -2 գործառույթների գծապատկերները: Տանգենտոիդի հիմնական ճյուղի վրա (նկ. 92) դրանք հատվում են x \u003d arctg (-2) կետում:

Ընտրեք x առանցքի միջակայքը, որի վրա շոշափողի հիմնական ճյուղը

Դիտարկենք tan x \u003d a- ի հավասարումը, որտեղ a\u003e 0: Y \u003d ctg x և y \u003d a գործառույթների գծապատկերներն անսահման շատ ընդհանուր կետեր ունեն, այս բոլոր կետերի abscissas- ները ձևի են. X \u003d x 1 + nk, որտեղ x 1 \u003d arcctg a- ը y \u003d a ուղիղ գծի հատման կետի abscissa- ն է `tangentoid- ի հիմնական ճյուղի հետ y \u003d a ուղիղ գծի հատման կետի abscissa (նկ. 93): Հետևաբար, arcctg a- ն այն թիվ է, որի կոթանգենտը հավասար է a- ին և որը պատկանում է (0, n) միջակայքին; Այս միջակայքի վրա կառուցված է y \u003d ctg x ֆունկցիայի գծապատկերի հիմնական ճյուղը:

Նկարում 93-ը ցույց է տալիս նաև c1tg \u003d -a հավասարման լուծման գրաֆիկական նկարազարդումը: Y \u003d ctg x և y \u003d -a գործառույթների գծապատկերներն անսահման շատ ընդհանուր կետեր ունեն, այս բոլոր կետերի abscissas- ն ունի x \u003d x 2 + nk ձև, որտեղ x 2 \u003d arcctg (- a) - ը y \u003d -a գծի հատման կետի abscissa է հիմնականի հետ տանգենտոիդ ճյուղը: Հետևաբար, arcctg (-a) - թիվ է, որի կոթանգը -a է և որը պատկանում է (O, n) ընդմիջմանը: Այս միջակայքի վրա կառուցվում է Y \u003d ctg x ֆունկցիայի գծապատկերի հիմնական ճյուղը:

Սահմանում 2.arcctg a (arc cotangent a) - մի թիվ է (0, n) միջակայքից, որի կոթանգանգը a է:
Այսպիսով,

Այժմ մենք կարող ենք ընդհանուր եզրակացություն անել ctg x \u003d a հավասարության լուծման վերաբերյալ. Ctg x \u003d a հավասարումը լուծումներ ունի.

Ուշադրություն դարձրեք (տես նկ. 93) ՝ x 2 \u003d n-x 1: Դա նշանակում է որ

Օրինակ 4. Հաշվել

Ա) Մենք դրեցինք

Ctg x \u003d a հավասարումը գրեթե միշտ կարող է փոխակերպվել ձևի: Բացառություն է ctg x \u003d 0 հավասարումը: Բայց այս դեպքում, օգտվելով այն փաստից, որ կարող ես գնալ
հավասարումը cos x \u003d 0: Այսպիսով, x \u003d a ձևի հավասարումը անկախ հետաքրքրություն չունի:

Ա.Գ. Մորդկովիչ հանրահաշիվ 10-րդ դասարան

Օրացույց-թեմատիկ պլանավորում մաթեմատիկայում, տեսանյութ մաթեմատիկայում առցանց, Մաթեմատիկա դպրոցում ներբեռնում

Դասի բովանդակությունը դասի ուրվագիծ աջակցություն շրջանակի դասի ներկայացման արագացման մեթոդների ինտերակտիվ տեխնոլոգիաներ Պրակտիկա առաջադրանքներ և վարժություններ ինքնաքննության սեմինարներ, դասընթացներ, դեպքեր, որոնումներ տնային առաջադրանքներ քննարկման հարցեր ուսանողների հռետորական հարցեր Պատկերազարդումներ աուդիո, տեսահոլովակներ և մուլտիմեդիա լուսանկարներ, նկարների գծապատկերներ, սեղաններ, սխեմաների հումոր, կատակներ, կատակներ, կոմիքսների առակներ, ասացվածքներ, խաչբառեր, մեջբերումներ Լրացումներ ամփոփագրեր հոդվածներ չիպսեր հետաքրքրաշարժ խաբեության թերթիկների դասագրքեր հիմնական և լրացուցիչ բառապաշար այլ բառերի համար Դասագրքերի և դասերի կատարելագործում ձեռնարկի սխալների շտկումներ Դասագրքում դասագրքում նորամուծության տարրերի մի հատվածի թարմացում ՝ հնացած գիտելիքները նորերով փոխարինելով Միայն ուսուցիչների համար կատարյալ դասեր քննարկման ծրագրի տարվա մեթոդական առաջարկների օրացուցային պլան Ինտեգրված դասեր

Earlierրագրի սկզբում ուսանողները գաղափար ստացան, թե ինչպես լուծել եռանկյունաչափական հավասարումներ, ծանոթացան հակադարձ կոսինուս և աղեղ հասկացություններին, cos t \u003d a և sin t \u003d a հավասարումների լուծումների օրինակներին: Տեսանյութի այս ձեռնարկում դիտարկեք լուծել tg x \u003d a և ctg x \u003d a հավասարումները:

Այս թեման ուսումնասիրելու սկզբում հաշվի առեք tg x \u003d 3 և tg x \u003d - 3. հավասարումները: Եթե tg x \u003d 3 հավասարումը լուծենք գրաֆիկի միջոցով, կտեսնենք, որ y \u003d tg x և y \u003d 3 գործառույթների գծապատկերների հատումը ունի անսահման լուծումների շարք, որտեղ x \u003d x 1 + πk. X 1 արժեքը y \u003d tg x և y \u003d 3 գործառույթների գծապատկերների հատման կետի x կոորդինատն է: Հեղինակը ներկայացնում է արքանգանգ հասկացությունը. Arctg 3-ը թիվ է, որի tg- ը 3 է, և այս թիվը պատկանում է -π / 2-ից π / 2 միջակայքին: Օգտագործելով arctangent հասկացությունը, tg x \u003d 3 հավասարման լուծումը կարող է գրվել որպես x \u003d arctan 3 + πk:

Ըստ անալոգիայի, լուծվում է tg x \u003d - 3. հավասարումը: Ըստ y \u003d tg x և y \u003d - 3 գործառույթների կառուցված գծապատկերների, կարելի է տեսնել, որ գծապատկերների խաչմերուկի կետերը, ուստի հավասարումների լուծումները կլինեն x \u003d x 2 + πk: Օգտագործելով արկանդագենտը, լուծումը կարող է գրվել որպես x \u003d arctan (- 3) + πk: Հաջորդ նկարում մենք կարող ենք տեսնել, որ arctan (- 3) \u003d - arctan 3:

Արկանգանտի ընդհանուր սահմանումը հետևյալն է. A- ի Arctangent- ը թիվ է -π / 2-ից π / 2-ի միջակայքից, որի տանգենսը հավասար է a- ի: Այնուհետեւ tg x \u003d a հավասարման լուծումը x \u003d arctan a + πk է:

Հեղինակը բերում է օրինակ 1. Գտեք arctg արտահայտության լուծումը: Ներկայացնենք նշումը. Համարի արխանգանդը հավասար է x- ին, ապա tg x- ը հավասար կլինի այս թվին, որտեղ x- ը պատկանում է -π / 2-ից π / 2 հատվածին: Ինչպես նախորդ թեմաների օրինակներում, մենք կօգտագործենք արժեքների աղյուսակ: Ըստ այս աղյուսակի, այս համարի տանգենսը համապատասխանում է x \u003d π / 3 արժեքին: Եկեք գրենք հավասարման լուծումը, տրված թվի կոլեկտորը հավասար է π / 3-ին, π / 3-ը նույնպես պատկանում է -π / 2-ից π / 2 միջակայքին:

Օրինակ 2 - Հաշվիր բացասական թվի արխիվը: Օգտագործելով հավասարություն arctan (- a) \u003d - arctan a, մուտքագրեք x արժեքը: 2-ի օրինակի նման, մենք գրում ենք x- ի արժեքը, որը պատկանում է -π / 2-ից π / 2 հատվածին: Արժեքների աղյուսակից մենք գտնում ենք, որ x \u003d π / 3, հետեւաբար, - tg x \u003d - π / 3: Հավասարության պատասխանն է `π / 3:

Դիտարկենք օրինակը 3. Լուծիր tan x \u003d 1. հավասարումը: Մենք գրում ենք, որ x \u003d arctan 1 + πk: Աղյուսակում tg 1 արժեքը համապատասխանում է x \u003d π / 4 արժեքին, հետեւաբար, arctan 1 \u003d π / 4: Այս արժեքը փոխարինեք x սկզբնական բանաձևում և գրեք x \u003d π / 4 + πk պատասխանը:

Օրինակ 4. հաշվարկեք tg x \u003d - 4.1: Այս դեպքում x \u003d արկտան (- 4.1) + πk: Որովհետեւ այս դեպքում հնարավոր չէ գտնել արկտանի արժեքը, պատասխանը նման կլինի x \u003d arctan (- 4,1) + πk:

5-րդ օրինակում դիտարկվում է tg x\u003e 1 անհավասարության լուծումը: Այն լուծելու համար մենք կառուցում ենք y \u003d tan x և y \u003d 1. գործառույթների գծապատկերները: Ինչպես տեսնում եք նկարում, այս գծապատկերները հատվում են x \u003d π / 4 + πk կետերում: Որովհետեւ այս դեպքում tg x\u003e 1, գծապատկերի վրա մենք ընտրում ենք տանգենտոիդի տարածքը, որը գտնվում է y \u003d 1 գծապատկերի վերևում, որտեղ x- ը պատկանում է π / 4-ից π / 2 միջակայքին: Պատասխանը գրում ենք π / 4 + πk< x < π/2 + πk.

Հաջորդը դիտարկենք ctg x \u003d a հավասարումը: Նկարում ներկայացված են y \u003d ctg x, y \u003d a, y \u003d - a գործառույթների գծապատկերներ, որոնք ունեն հատման շատ կետեր: Լուծումները կարող են գրվել x \u003d x 1 + πk, որտեղ x 1 \u003d arcctg a և x \u003d x 2 + πk, որտեղ x 2 \u003d arcctg (- a): Նշվում է, որ x 2 \u003d π - x 1: Սա ենթադրում է հավասարություն arcctg (- a) \u003d π - arcctg a. Դրանից հետո տրված է աղեղային կոտոշկի սահմանում. Աղեղային կոտոշկանը a- ն 0-ից π- ի միջակայքից համարվող թիվ է, որի կոտանգանգը հավասար է a- ի: Ctg x \u003d a հավասարման լուծումը գրվում է այսպես ՝ x \u003d arcctg a + πk:

Տեսադասի ավարտին արվում է ևս մեկ կարևոր եզրակացություն. Ctg x \u003d a արտահայտությունը կարելի է գրել tg x \u003d 1 / a ձևով, պայմանով, որ a- ն հավասար չէ զրոյի:

ՏԵՔՍՏԱՅԻՆ ԿՈԴ

Դիտարկենք tan x \u003d 3 և tan x \u003d - 3. հավասարումների լուծումը. Գծապատկերով լուծելով առաջին հավասարումը ՝ մենք տեսնում ենք, որ y \u003d tan x և y \u003d 3 գործառույթների գծապատկերներն ունեն անսահմանորեն հատման կետեր, որոնց abscissas- երը գրված են

x \u003d x 1 + πk, որտեղ x 1 - ը y \u003d 3 ուղիղ գծի հատման կետի աբսիսսա է տանգենտոիդի հիմնական ճյուղի հետ (նկ. 1), որի համար նշումը ստեղծվել է

arctan 3 (Arctangent երեք):

Ինչպե՞ս ես հասկանում arctg 3-ը:

Սա մի թիվ է, որի տանգենսը 3 է, և այս թիվը պատկանում է ընդմիջմանը (-;): Այդ դեպքում tan x \u003d 3 հավասարման բոլոր արմատները կարող են գրվել x \u003d arctan 3 + πk բանաձևով:

Նմանապես, tan х \u003d - 3 հավասարության լուծումը կարող է գրվել х \u003d х 2 + πk ձևով, որտեղ х 2 - ը \u003d \u003d 3 ուղիղ գծի խաչմերուկի կետի աբսիսսա է տանգենտոիդի հիմնական ճյուղի հետ (նկ. 1), որի համար նշվում է արկտան (- 3) (arctangent մինուս երեք): Այդ դեպքում հավասարման բոլոր արմատները կարող են գրվել բանաձևով. X \u003d արկտան (-3) + πk: Նկարը ցույց է տալիս, որ arctan (- 3) \u003d - arctan 3:

Եկեք ձեւակերպենք արխանգանտի սահմանումը: A արկանկանգը (-;) ընդմիջումից մի թիվ է, որի տանգենսը հավասար է a- ի:

Հավասարությունը հաճախ օգտագործվում է. Arctan (-a) \u003d -arctan a, ինչը ճիշտ է ցանկացած a- ի համար:

Իմանալով արկանդագնի սահմանումը ՝ մենք ընդհանուր եզրակացություն ենք անում հավասարումը լուծելու մասին

tg x \u003d a: tg x \u003d a հավասարումը ունի x \u003d arctan a + πk լուծում:

Եկեք քննարկենք մի քանի օրինակներ:

ՕՐԻՆԱԿ 1 Հաշվարկել arctg- ը:

Որոշում: Եկեք արկտանը \u003d x, ապա tgx \u003d և xϵ (-;): Showուցադրել արժեքների աղյուսակը Հետևաբար, x \u003d, քանի որ tg \u003d և ϵ (-;):

Այսպիսով, arctg \u003d:

ՕՐԻՆԱԿ 2. Հաշվեք արկտանը (-):

Որոշում: Օգտագործելով հավասարություն arctan (- a) \u003d - arctan a, մենք գրում ենք.

arctg (-) \u003d - arctg: Եկեք - arctan \u003d x, ապա - tgx \u003d և xϵ (-;): Հետևաբար, x \u003d, քանի որ tg \u003d և ϵ (-;): Showուցադրել արժեքների աղյուսակը

Հետևաբար - արկտան \u003d - tgх \u003d -:

ՕՐԻՆԱԿ 3. Լուծել tgx \u003d 1 հավասարումը:

1.Գրենք լուծումների բանաձևը. Х \u003d արկտան 1 + πk:

2. Գտեք արխանգանտի արժեքը

քանի որ tg \u003d. Showուցադրել արժեքների աղյուսակը

Այստեղից arctg1 \u003d:

3. Գտած արժեքը դնենք լուծումների բանաձևում.

ՕՐԻՆԱԿ 4. Լուծել tgx \u003d - 4.1 հավասարումը (տանգենտ x- ը հավասար է մինուս չորս ամբողջ մեկ տասներորդին):

Որոշում: Եկեք գրենք լուծումների բանաձևը. X \u003d արկտան (- 4.1) + πk:

Մենք չենք կարող հաշվարկել արխանգանտի արժեքը, ուստի հավասարման լուծումը կթողնենք ստացված տեսքով:

ՕՐԻՆԱԿ 5. Լուծեք անհավասարությունը tgх 1:

Որոշում: Մենք գրաֆիկորեն կլուծենք:

1. Եկեք կառուցենք տանգենսոիդ

y \u003d tanx և ուղիղ y \u003d 1 (նկ. 2): Նրանք հատվում են х \u003d + πk ձևի կետերում:

2. Ընտրեք x առանցքի միջակայքը, որի վրա գտնվում է տանգենտոիդի հիմնական ճյուղը y \u003d 1 ուղիղ գծի վերևում, քանի որ tgx 1. պայմանով. Սա է ընդմիջումը (;):

3. Մենք օգտագործում ենք ֆունկցիայի պարբերականությունը:

Հատկություն 2. y \u003d tg x պարբերական ֆունկցիա է π հիմնական ժամանակահատվածի հետ:

Հաշվի առնելով y \u003d tgx գործառույթի պարբերականությունը, մենք գրում ենք պատասխանը.

(;) Պատասխանը կարելի է գրել որպես կրկնակի անհավասարություն.

Մենք անցնում ենք ctg x \u003d a հավասարմանը: Ներկայացնենք դրական և բացասական ա – ների հավասարության լուծման գրաֆիկական նկարագրություն (նկ. 3):

Y \u003d ctg x և y \u003d a և. Գործառույթների գծապատկերներ

y \u003d ctg x և y \u003d -a

ունեն անսահման շատ ընդհանուր կետեր, որոնց աբսցիսներն են.

x \u003d x 1 +, որտեղ x 1 - ը y \u003d a ուղիղ գծի հատման կետի աբսիսս է `տանգենտոիդի հիմնական ճյուղի հետ և

x 1 \u003d arcсtg a;

x \u003d x 2 +, որտեղ x 2 - գծի հատման կետի աբսիսսա է

y \u003d - a ՝ տանգենտոիդի հիմնական ճյուղով և x 2 \u003d arcсtg (- ա):

Նշենք, որ x 2 \u003d π - x 1: Այսպիսով, եկեք գրենք մի կարևոր հավասարություն.

arcсtg (-а) \u003d π - arcсtg а.

Ձևակերպենք սահմանումը. Աղեղը կոտոշկանը a- ն է (0; π) ընդմիջումից մի թիվ, որի կոտանգանգը հավասար է a- ին:

Ctg x \u003d a հավասարման լուծումը գրված է տեսքով ՝ x \u003d arcctg a +:

Նշենք, որ ctg x \u003d a հավասարումը կարող է փոխակերպվել ձևի

tg x \u003d, բացառությամբ այն դեպքերի, երբ a \u003d 0:

Այս դասում մենք կշարունակենք ուսումնասիրել arcangent- ը և լուծել tg x \u003d a ձևի հավասարումներ ցանկացած a- ի համար: Դասի սկզբում մենք հավասարումը կլուծենք աղյուսակային արժեքով և լուծումը կպատկերացնենք գրաֆիկի վրա, այնուհետև շրջանագծի վրա: Հաջորդը, մենք tgx \u003d a հավասարումը լուծում ենք ընդհանուր ձևով և բերում ենք պատասխանի ընդհանուր բանաձևը: Մենք նկարազարդելու ենք գրաֆիկի և շրջանի վրա հաշվարկները և դիտարկենք պատասխանի տարբեր ձևերը: Դասի վերջում մենք լուծելու ենք մի քանի խնդիրներ գրաֆիկի և օղակի վրա լուծումների նկարագրությամբ:

Թեմա ՝ Եռանկյունաչափական հավասարումներ

Դաս. Կամարի տանգենս և լուծում է tgx \u003d a հավասարումը (շարունակություն)

1. Դասի թեման, ներածություն

Այս դասում մենք կանդրադառնանք ցանկացած իրականի համար հավասարության լուծմանը

2. tgx \u003d √3 հավասարման լուծում

Խնդիր 1. Լուծիր հավասարումը

Եկեք գտնենք լուծում ՝ օգտագործելով ֆունկցիաների գրաֆիկները (նկ. 1):

Հաշվի առեք ընդմիջումը Այս միջակայքի վրա գործառույթը միատոն է, ինչը նշանակում է, որ այն ձեռք է բերվում միայն ֆունկցիայի մեկ արժեքի համար:

Պատասխան.

Եկեք լուծենք նույն հավասարումը `օգտագործելով թվային շրջան (նկ. 2):

Պատասխան.

3. tgx \u003d a հավասարման լուծում ընդհանուր տեսքով

Եկեք լուծումը լուծենք ընդհանուր տեսքով (նկ. 3):

Ընդմիջման վրա հավասարումը եզակի լուծում ունի

Ամենափոքր դրական ժամանակահատվածը

Եկեք նկարազարդենք թվային շրջանի վրա (նկ. 4):

4. Խնդիրների լուծում

Խնդիր 2. Լուծիր հավասարումը

Փոխել փոփոխականը

Առաջադրանք 3. Լուծել համակարգը.

Լուծում (նկ. 5):

Կետում արժեքը հետևաբար համակարգի լուծումն է միայն կետը

Պատասխան.

Խնդիր 4. Լուծիր հավասարումը

Եկեք լուծենք փոփոխական փոփոխելով.

Խնդիր 5. Գտեք հավասարման լուծումների քանակը ընդմիջման վրա

Եկեք լուծենք խնդիրը ՝ օգտագործելով գրաֆիկը (նկ. 6):

Հավասարությունն ունի երեք լուծում տրված ընդմիջման վրա:

Եկեք նկարազարդենք թվային շրջանի վրա (նկ. 7), չնայած դա այնքան էլ պարզ չէ, ինչպես գծապատկերում:

Պատասխան. Երեք լուծում:

5. Եզրակացություն, եզրակացություն

Մենք լուծեցինք հավասարումը ցանկացած իրականի համար `օգտագործելով arctangent հասկացությունը: Հաջորդ դասին մենք կծանոթանանք աղեղային կոտանգենտ հասկացությանը:

Հղումների ցուցակ

1. Հանրահաշիվ և վերլուծության սկիզբ, 10-րդ դասարան (երկու մասով): Ուսումնական հաստատությունների դասագիրք (պրոֆիլի մակարդակ), խմբ. Ա.Գ.Մորդկովիչ -Մ. ՝ Մնեմոսինա, 2009 թ.

2. Հանրահաշիվ և վերլուծության սկիզբ, 10-րդ դասարան (երկու մասով): Խնդրագիրք ուսումնական հաստատությունների համար (պրոֆիլի մակարդակ), խմբ. Ա.Գ.Մորդկովիչ -Մ. ՝ Մնեմոսինա, 2007:

3. Vilenkin N. Ya., Ivashev-Musatov OS, Schwarzburd SI հանրահաշիվ և մաթեմատիկական վերլուծություն 10-րդ դասարանի համար (դասագիրք դպրոցների և մաթեմատիկայի առաջադեմ ուսումնասիրություն ունեցող դասարանների աշակերտների համար): - Մ., Կրթություն, 1996:

4. Galitsky M. L., Moshkovich M. M., Shvartsburd S. I. հանրահաշվի և մաթեմատիկական վերլուծության խորը ուսումնասիրություն: - Մ., Կրթություն, 1997:

5. Բարձրագույն ուսումնական հաստատություններ դիմորդների մաթեմատիկայի խնդիրների հավաքագրում (M. I. Skanavi- ի խմբագրությամբ): - Մ .: Բարձրագույն դպրոց, 1992:

6. Մերզլյակ Ա. Գ., Պոլոնսկի Վ. Բ., Յակիր Մ. Ս. Հանրահաշվական սիմուլյատոր: - Կ. Ա. Ս. Կ., 1997 թ.

7. Sahakyan S.M., Goldman A.M., Denisov D.V. Հանրահաշվի խնդիրները և վերլուծության սկզբունքները (ձեռնարկ հանրակրթական հաստատությունների 10-11-րդ դասարանների աշակերտների համար): - Մ., Կրթություն, 2003 թ.

8. Karp AP Հանրահաշվի հիմնախնդիրների ժողովածուն և վերլուծության սկզբունքները. Դասագիրք: 10-11 դասարանների նպաստ խորացումով ուսումնասիրել մաթեմատիկա.-Մ., կրթություն, 2006 թ.

Տնային աշխատանք

Հանրահաշիվ և վերլուծության սկիզբ, 10-րդ դասարան (երկու մասով): Խնդրագիրք ուսումնական հաստատությունների համար (պրոֆիլի մակարդակ), խմբ. Ա.Գ.Մորդկովիչ -Մ. ՝ Մնեմոսինա, 2007:

№№ 22.18, 22.21.

Լրացուցիչ վեբ ռեսուրսներ

1. Մաթեմատիկա:

2. Ինտերնետային պորտալի խնդիրները: ru

3. Քննություններին պատրաստվելու ուսումնական պորտալ:

Կարող եք պատվիրել ձեր խնդրի մանրամասն լուծում:

Եռանկյունաչափական ֆունկցիայի նշանի տակ անհայտ պարունակող հավասարությունը (`sin x, cos x, tan x` կամ` ctg x`) կոչվում է եռանկյունաչափական հավասարություն, և դրանց բանաձևերը հետագայում կքննարկենք:

Ամենապարզ հավասարումները կոչվում են `sin x \u003d a, cos x \u003d a, tg x \u003d a, ctg x \u003d a`, որտեղ` x` - գտնվող անկյունը, ʻa` - ցանկացած թիվ: Եկեք գրենք դրանցից յուրաքանչյուրի արմատային բանաձեւերը:

1. «sin x \u003d a» հավասարումը:

For `| a |\u003e 1` լուծումներ չունի:

Համար `| ա | \\ leq 1` անվերջ քանակությամբ լուծումներ ունի:

Արմատային բանաձև. «X \u003d (- 1) ^ n arcsin a + \\ pi n, n \\ in Z»

2. «cos x \u003d a» հավասարումը

«| A |\u003e 1» -ի համար - ինչպես սինուսի դեպքում, այն իրական թվերի մեջ լուծումներ չունի:

Համար `| ա | \\ leq 1` անվերջ քանակությամբ լուծումներ ունի:

Արմատային բանաձև. «X \u003d \\ pm arccos a + 2 \\ pi n, n \\ in Z»

Սինուսի և կոսինուսի հատուկ դեպքեր գծապատկերներում:

3. «tg x \u003d a» հավասարումը

Ունի անսահման քանակությամբ լուծումներ `a`- ի ցանկացած արժեքների համար:

Արմատային բանաձև. «X \u003d arctan a + \\ pi n, n \\ in Z»

4. «ctg x \u003d a» հավասարումը

Նաև ունի անսահման թվով լուծումներ `a`- ի ցանկացած արժեքների համար:

Արմատային բանաձև. «X \u003d arcctg a + \\ pi n, n \\ Z- ում»

Եռանկյունաչափական հավասարումների արմատների համար բանաձևեր աղյուսակում

Սինուսի համար.
Կոսինուսի համար.
Տանգենցի և կոթանգենի համար.
Հակադարձ եռանկյունաչափական գործառույթներ պարունակող հավասարումների լուծման բանաձևեր.

Եռանկյունաչափական հավասարումների լուծման մեթոդներ

Trigանկացած եռանկյունաչափական հավասարության լուծումը բաղկացած է երկու փուլից.

• օգտագործելով այն դարձնել ամենապարզը;
• լուծեք ստացված ամենապարզ հավասարումը ՝ օգտագործելով վերը գրված արմատային բանաձևերն ու աղյուսակները:

Եկեք նայենք լուծման հիմնական մեթոդների օրինակներին:

Հանրահաշվական մեթոդ:

Այս մեթոդով կատարվում է փոփոխական փոխարինում և հավասարության մեջ փոխարինում:

Օրինակ. Լուծեք հավասարումը. «2cos ^ 2 (x + \\ frac \\ pi 6) -3sin (\\ frac \\ pi 3 - x) + 1 \u003d 0»

«2cos ^ 2 (x + \\ frac \\ pi 6) -3cos (x + \\ frac \\ pi 6) + 1 \u003d 0»,

մենք կատարում ենք փոփոխությունը. `cos (x + \\ frac \\ pi 6) \u003d y`, ապա` 2y ^ 2-3y + 1 \u003d 0`,

մենք գտնում ենք արմատները. «y_1 \u003d 1, y_2 \u003d 1/2», որից հետո գալիս է երկու դեպք.

1. `cos (x + \\ frac \\ pi 6) \u003d 1`,` x + \\ frac \\ pi 6 \u003d 2 \\ pi n`, `x_1 \u003d - \\ frac \\ pi 6 + 2 \\ pi n`

2. `cos (x + \\ frac \\ pi 6) \u003d 1 / 2`,` x + \\ frac \\ pi 6 \u003d \\ pm arccos 1/2 + 2 \\ pi n`, `x_2 \u003d \\ pm \\ frac \\ pi 3- \\ frac \\ pi 6 + 2 \\ pi n`:

Պատասխան. `X_1 \u003d - \\ frac \\ pi 6 + 2 \\ pi n`,` x_2 \u003d \\ pm \\ frac \\ pi 3- \\ frac \\ pi 6 + 2 \\ pi n`.

Գործոնավորում:

Օրինակ. Լուծեք հավասարումը. `Sin x + cos x \u003d 1`

Որոշում: Հավասարության բոլոր պայմանները տեղափոխեք ձախ ՝ `sin x + cos x-1 \u003d 0` Ձախ կողմը օգտագործելով, վերափոխելով և գործոնով.

`sin x - 2sin ^ 2 x / 2 \u003d 0`,

`2sin x / 2 cos x / 2-2sin ^ 2 x / 2 \u003d 0`,

`2sin x / 2 (cos x / 2-sin x / 2) \u003d 0`,

1. `sin x / 2 \u003d 0`,` x / 2 \u003d \\ pi n`, `x_1 \u003d 2 \\ pi n`:
2. `cos x / 2-sin x / 2 \u003d 0`,` tg x / 2 \u003d 1`, `x / 2 \u003d arctan 1+ \\ pi n`,` x / 2 \u003d \\ pi / 4 + \\ pi n` , `x_2 \u003d \\ pi / 2 + 2 \\ pi n`:

Պատասխան. `X_1 \u003d 2 \\ pi n`,` x_2 \u003d \\ pi / 2 + 2 \\ pi n`:

Նվազեցում միատարր հավասարման

Նախ, անհրաժեշտ է այս եռանկյունաչափական հավասարումը բերել երկու տեսակներից մեկին.

SinA sin x + b cos x \u003d 0` (առաջին աստիճանի միատարր հավասարություն) կամ ʻa sin ^ 2 x + b sin x cos x + c cos ^ 2 x \u003d 0` (երկրորդ աստիճանի միատարր հավասարություն):

Հետո երկու մասերն էլ բաժանիր `cos x \\ ne 0` - առաջին դեպքում, և ըստ` cos ^ 2 x \\ ne 0` - երկրորդի համար: Մենք ստանում ենք հավասարումներ `tg x`- ի համար` ʻa tg x + b \u003d 0` և ʻa tg ^ 2 x + b tg x + c \u003d 0`, որոնք անհրաժեշտ է լուծել հայտնի մեթոդներով:

Օրինակ. Լուծեք հավասարումը. «2 sin ^ 2 x + sin x cos x - cos ^ 2 x \u003d 1»:

Որոշում: Աջ կողմը վերաշարադրել ՝ «1 \u003d sin ^ 2 x + cos ^ 2 x»:

«2 sin ^ 2 x + sin x cos x - cos ^ 2 x \u003d" մեղք ^ 2 x + cos ^ 2 x ",

`2 sin ^ 2 x + sin x cos x - cos ^ 2 x-" `sin ^ 2 x - cos ^ 2 x \u003d 0`

`sin ^ 2 x + sin x cos x - 2 cos ^ 2 x \u003d 0`:

Սա երկրորդ աստիճանի միատարր եռանկյունաչափական հավասարություն է, մենք նրա ձախ և աջ կողմերը բաժանում ենք `cos ^ 2 x \\ ne 0`, մենք ստանում ենք.

«\\ frac (sin ^ 2 x) (cos ^ 2 x) + \\ frac (sin x cos x) (cos ^ 2 x) - \\ frac (2 cos ^ 2 x) (cos ^ 2 x) \u003d 0»

`tg ^ 2 x + tg x - 2 \u003d 0` Եկեք ներկայացնենք `tg x \u003d t` փոխարինումը, որպես արդյունք` `t ^ 2 + t - 2 \u003d 0`: Այս հավասարման արմատներն են `t_1 \u003d -2` և` t_2 \u003d 1`: Հետո.

1. `tg x \u003d -2`,` x_1 \u003d arctg (-2) + \\ pi n`, `n \\ in Z`
2. `tg x \u003d 1`,` x \u003d arctan 1+ \\ pi n`, `x_2 \u003d \\ pi / 4 + \\ pi n`,` n \\ in Z`

Պատասխանել `x_1 \u003d arctg (-2) + \\ pi n`,` n \\ in Z`, `x_2 \u003d \\ pi / 4 + \\ pi n`,` n \\ in Z`:

Գնացեք կես անկյուն

Օրինակ. Լուծեք հավասարումը. «11 sin x - 2 cos x \u003d 10»:

Որոշում: Արդյունքում կիրառեք կրկնակի անկյան բանաձևերը. «22 sin (x / 2) cos (x / 2)-» 2 cos ^ 2 x / 2 + 2 sin ^ 2 x / 2 \u003d «10 sin ^ 2 x / 2 +10 կոս ^ 2 x / 2`

`4 tg ^ 2 x / 2 - 11 tg x / 2 + 6 \u003d 0`

Կիրառելով վերը նշված հանրահաշվական մեթոդը `մենք ստանում ենք.

1. `tg x / 2 \u003d 2`,` x_1 \u003d 2 arctan 2 + 2 \\ pi n`, `n \\ in Z`,
2. `tg x / 2 \u003d 3 / 4`,` x_2 \u003d arctan 3/4 + 2 \\ pi n`, `n \\ in Z`:

Պատասխանել `x_1 \u003d 2 arctan 2 + 2 \\ pi n, n \\ in Z`,` x_2 \u003d arctan 3/4 + 2 \\ pi n`, `n \\ in Z`:

Ներկայացրե՛ք օժանդակ անկյուն

ʻA sin x + b cos x \u003d c` եռանկյունաչափական հավասարում, որտեղ a, b, c գործակիցներ են, և x փոփոխական է, մենք երկու կողմերն էլ բաժանում ենք «sqrt (a ^ 2 + b ^ 2)».

«\\ frac a (sqrt (a ^ 2 + b ^ 2)) sin x +" \\ frac b (sqrt (a ^ 2 + b ^ 2)) cos x \u003d "\\ frac c (sqrt (a ^ 2 + բ ^ 2)) »:

Ձախ գործակիցները ունեն սինուսի և կոսինուսի հատկություններ, այսինքն ՝ դրանց քառակուսիների գումարը հավասար է 1-ի, իսկ մոդուլները 1-ից մեծ չեն: Եկեք դրանք նշենք հետևյալ կերպ. , "\\ frac b (sqrt (a ^ 2 + b ^ 2)) \u003d sin \\ varphi", "\\ frac c (sqrt (a ^ 2 + b ^ 2)) \u003d C", ապա ՝

`cos \\ varphi sin x + sin \\ varphi cos x \u003d C`:

Եկեք ավելի սերտ նայենք հետևյալ օրինակը.

Օրինակ. Լուծեք հավասարումը. «3 sin x + 4 cos x \u003d 2»:

Որոշում: Հավասարության երկու կողմերն էլ բաժանեք «sqrt (3 ^ 2 + 4 ^ 2)» -ով, կստանանք.

"\\ frac (3 sin x) (sqrt (3 ^ 2 + 4 ^ 2)) +" \\ frac (4 cos x) (sqrt (3 ^ 2 + 4 ^ 2)) \u003d "\\ frac 2 (sqrt (3 ^ 2 + 4 ^ 2)) »

`3/5 sin x + 4/5 cos x \u003d 2 / 5`:

Եկեք նշենք `3/5 \u003d cos \\ varphi`,` 4/5 \u003d sin \\ varphi`: Քանի որ `sin \\ varphi\u003e 0`,` cos \\ varphi\u003e 0`, ապա որպես օժանդակ անկյուն վերցնում ենք `\\ varphi \u003d arcsin 4 / 5`: Դրանից հետո մենք գրում ենք մեր հավասարությունը տեսքով.

`cos \\ varphi sin x + sin \\ varphi cos x \u003d 2 / 5`

Կիրառելով սինուսի անկյունների գումարի բանաձևը `մենք գրում ենք մեր հավասարությունը հետևյալ ձևով.

`sin (x + \\ varphi) \u003d 2 / 5`,

`x + \\ varphi \u003d (- 1) ^ n arcsin 2/5 + \\ pi n`,` n \\ in Z`,

`x \u003d (- 1) ^ n arcsin 2/5-` ʻarcsin 4/5 + \\ pi n`, `n \\ in Z`:

Պատասխանել `x \u003d (- 1) ^ n arcsin 2/5-` ʻarcsin 4/5 + \\ pi n`, `n \\ in Z`:

Կոտորակային-ռացիոնալ եռանկյունաչափական հավասարումներ

Սրանք հավասարություններ են կոտորակների հետ, որոնց համարիչներն ու հայտարարները եռանկյունաչափական ֆունկցիաներ ունեն:

Օրինակ. Լուծիր հավասարումը: «\\ frac (sin x) (1 + cos x) \u003d 1-cos x»:

Որոշում: Բազմապատկել և բաժանել հավասարության աջ կողմը `` (1 + cos x) `-ով: Արդյունքում, մենք ստանում ենք.

«\\ frac (sin x) (1 + cos x) \u003d" \\ frac ((1-cos x) (1 + cos x)) (1 + cos x) "

«\\ frac (sin x) (1 + cos x) \u003d" \\ frac (1-cos ^ 2 x) (1 + cos x) "

«\\ frac (sin x) (1 + cos x) \u003d" \\ frac (sin ^ 2 x) (1 + cos x) "

"\\ frac (sin x) (1 + cos x)-" "frac (sin ^ 2 x) (1 + cos x) \u003d 0"

«\\ frac (sin x-sin ^ 2 x) (1 + cos x) \u003d 0»

Հաշվի առնելով, որ հայտարարը չի կարող հավասար լինել զրոյի, Z- ում մենք ստանում ենք «1 + cos x \\ ne 0», «cos x \\ ne -1», «x \\ ne \\ pi + 2 \\ pi n, n \\»:

Կոտորակի համարիչը հավասարեցրու զրոյի `` sin x-sin ^ 2 x \u003d 0`, `sin x (1-sin x) \u003d 0`: Հետո `sin x \u003d 0` կամ` 1-sin x \u003d 0`:

1. `sin x \u003d 0`,` x \u003d \\ pi n`, `n \\ in Z`
2. `1-sin x \u003d 0`,` sin x \u003d -1`, `x \u003d \\ pi / 2 + 2 \\ pi n, n \\ in Z`:

Հաշվի առնելով, որ «x \\ ne \\ pi + 2 \\ pi n, n \\ in Z», լուծումներն են `x \u003d 2 \\ pi n, n \\ in Z` և« x \u003d \\ pi / 2 + 2 \\ pi n » , `n \\ in Z`:

Պատասխանել `x \u003d 2 \\ pi n`,` n \\ in Z`, `x \u003d \\ pi / 2 + 2 \\ pi n`,` n \\ in Z`:

Եռանկյունաչափությունը և մասնավորապես եռանկյունաչափական հավասարումները օգտագործվում են երկրաչափության, ֆիզիկայի, ճարտարագիտության գրեթե բոլոր բնագավառներում: Ուսումնասիրությունը սկսվում է 10-րդ դասարանից, քննության համար հաստատ առաջադրանքներ կան, ուստի փորձեք հիշել եռանկյունաչափական հավասարումների բոլոր բանաձևերը. Դրանք անպայման օգտակար կլինեն:

Այնուամենայնիվ, նույնիսկ անհրաժեշտ չէ դրանք անգիր սովորել, գլխավորն այն է, որ հասկանաս էությունը և կարողանաս եզրակացնել: Դա այնքան էլ դժվար չէ, որքան թվում է: Ինքներդ դիտեք ՝ դիտելով տեսանյութը: