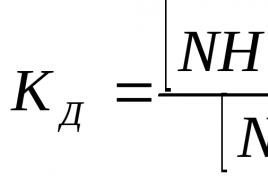Przykłady układów równań liniowych: metoda rozwiązywania. Algorytm rozwiązywania równań wymiernych Algorytm rozwiązywania prostych równań

„Metoda Gaussa i Cramera” - metoda Gaussa. Podstawowe przemiany. Podzielmy pierwsze równanie układu (1) przez a11. (pięć). Gauss zmarł 23 lutego 1855 roku w Getyndze. Metoda Gaussa jest klasyczną metodą rozwiązywania układu liniowych równań algebraicznych. Następnie x2 i x3 są podstawiane do pierwszego równania i znajduje się x1. Niech współczynnik.

„Równania i nierówności” - Polega na: wykreśleniu w tym samym układzie współrzędnych wykresów dwóch funkcji. 4. Graficzna metoda wyznaczania liczby pierwiastków równania. 3. Ile pierwiastków ma równanie? 2. Znajdź sumę liczb, które spełniają nierówność. Rozwiązanie systemu graficznie. 3. Znajdź przedział zawierający największą liczbę całkowitą spełniającą nierówność.

„Twierdzenie Gaussa-Markowa” - Udowodnijmy, że szacunki (7.3) są bezstronne. Sformułujmy wektory i macierz współczynników w oparciu o układ (7.2). Jeżeli macierz X jest niekoliniowa, a wektor zaburzeń losowych spełnia następujące wymagania: Gdzie. (7,7). Aby uzyskać warunek konieczny dla ekstremum, różnicujemy (7.6) ze względu na wektor parametrów.

„Metody rozwiązywania układów równań” - B. 1. Oblicz: 14. 6. Jaki procent stanowi liczba 8 z jej kwadratu? 12. 7. Znajdź największy pierwiastek równania. 9. Którą funkcję przedstawia rysunek? Znajdź znaczenie wyrażenia. %. H. O. B. 15x + 10 (1 - x) \u003d 1.

„Irracjonalne równanie” - znajdź błąd. Równania, w których zmienna znajduje się pod znakiem pierwiastka, nazywane są nieracjonalnymi. ? X - 6 \u003d 2? x - 3 \u003d 0? x + 4 \u003d 7? 5 - x \u003d 0? 2 - x \u003d x + 4. PROBLEM: Uczniowie nie zawsze wiedzą, jak świadomie wykorzystywać informacje o równaniach niewymiernych. Czy liczba x jest pierwiastkiem równania: a)? x - 2 \u003d? 2 - x, x0 \u003d 4 b)? 2 - x \u003d? x - 2, x0 \u003d 2 c)? x - 5 \u003d? 2x - 13, x0 \u003d 6 d)? 1 - x \u003d? 1 + x, x0 \u003d 0.

„Rozwiązywanie równań z parametrem” - Rozwiązanie. Przykład. 6 klasa. Przykłady: W piątej klasie, powtarzając właściwości liczb, możesz rozważyć przykłady. Na zajęciach pozalekcyjnych z matematyki w klasie VI rozważane jest rozwiązanie równań o parametrach postaci: 1) ax \u003d 6 2) (a - 1) x \u003d 8,3 3) bx \u003d -5. Przy a \u003d -1/2 otrzymujemy równanie 0x \u003d 0. Równanie ma nieskończony zbiór rozwiązań.

W sumie jest 49 prezentacji

Mówiąc najprościej, są to równania, w których istnieje co najmniej jedno ze zmienną w mianowniku.

Na przykład:

\\ (\\ frac (9x ^ 2-1) (3x) \\) \\ (\u003d 0 \\)
\\ (\\ frac (1) (2x) + \\ frac (x) (x + 1) \u003d \\ frac (1) (2) \\)
\\ (\\ frac (6) (x + 1) \u003d \\ frac (x ^ 2-5x) (x + 1) \\)

Przykład nie ułamkowe równania wymierne:

\\ (\\ frac (9x ^ 2-1) (3) \\) \\ (\u003d 0 \\)
\\ (\\ frac (x) (2) \\) \\ (+ 8x ^ 2 \u003d 6 \\)

Jak rozwiązuje się ułamkowe równania wymierne?

Najważniejszą rzeczą do zapamiętania o ułamkowych równaniach wymiernych jest zapisanie w nich. A po znalezieniu korzeni sprawdź je pod kątem dopuszczalności. W przeciwnym razie mogą pojawić się obce korzenie, a cała decyzja zostanie uznana za nieprawidłową.

Algorytm rozwiązywania ułamkowego równania wymiernego:

Zapisz i „rozwiąż” DHS.

Pomnóż każdy wyraz w równaniu przez wspólny mianownik i anuluj otrzymane ułamki. Mianowniki znikną.

Zapisz równanie bez otwierania nawiasów.

Rozwiąż wynikowe równanie.

Sprawdź znalezione korzenie za pomocą ODZ.

W odpowiedzi zapisz korzenie, które przeszły kontrolę w kroku 7.

Nie zapamiętuj algorytmu, 3-5 rozwiązanych równań - a sam zostanie zapamiętany.

Przykład ... Rozwiąż ułamkowe równanie wymierne \\ (\\ frac (x) (x-2) - \\ frac (7) (x + 2) \u003d \\ frac (8) (x ^ 2-4) \\)

Decyzja:

Odpowiedź: \(3\).

Przykład ... Znajdź pierwiastki ułamkowego równania wymiernego \\ (\u003d 0 \\)

Decyzja:

\\ (\\ frac (x) (x + 2) + \\ frac (x + 1) (x + 5) - \\ frac (7-x) (x ^ 2 + 7x + 10) \\)\(=0\) ODZ: \\ (x + 2 ≠ 0⇔x ≠ -2 \\) \\ (x + 5 ≠ 0 ⇔x ≠ -5 \\) \\ (x ^ 2 + 7x + 10 ≠ 0 \\) \\ (D \u003d 49-4 \\ cdot 10 \u003d 9 \\) \\ (x_1 ≠ \\ frac (-7 + 3) (2) \u003d - 2 \\) \\ (x_2 ≠ \\ frac (-7-3) (2) \u003d - 5 \\)		Zapisujemy i „rozwiązujemy” ODZ. Rozwiń \\ (x ^ 2 + 7x + 10 \\) według wzoru: \\ (ax ^ 2 + bx + c \u003d a (x-x_1) (x-x_2) \\). Na szczęście znaleźliśmy już \\ (x_1 \\) i \\ (x_2 \\).
\\ (\\ frac (x) (x + 2) + \\ frac (x + 1) (x + 5) - \\ frac (7-x) ((x + 2) (x + 5)) \\)\(=0\)		Oczywiście wspólnym mianownikiem ułamków jest \\ ((x + 2) (x + 5) \\). Mnożymy przez to całe równanie.
\\ (\\ frac (x (x + 2) (x + 5)) (x + 2) + \\ frac ((x + 1) (x + 2) (x + 5)) (x + 5) - \\) \\ (- \\ frac ((7-x) (x + 2) (x + 5)) ((x + 2) (x + 5)) \\)\(=0\)		Zmniejszanie frakcji
\\ (x (x + 5) + (x + 1) (x + 2) -7 + x \u003d 0 \\)		Rozwiń nawiasy
\\ (x ^ 2 + 5x + x ^ 2 + 3x + 2-7 + x \u003d 0 \\)		Podajemy podobne warunki
\\ (2x ^ 2 + 9x-5 \u003d 0 \\)		Znajdź korzenie równania
\\ (x_1 \u003d -5; \\) \\ (x_2 \u003d \\ frac (1) (2). \\)		Jeden z pierwiastków nie pasuje do ODZ, więc w odpowiedzi zapisujemy tylko drugi pierwiastek.

Odpowiedź: \\ (\\ frac (1) (2) \\).

Wyrażenia wymierne i równania racjonalne

Nauczyliśmy się już rozwiązywać równania kwadratowe. Teraz rozszerzmy badane metody o równania racjonalne.

Co to jest racjonalna ekspresja? Napotkaliśmy już tę koncepcję. Wyrażenia racjonalne nazywane są wyrażenia złożone z liczb, zmiennych, ich stopni i znaków operacji matematycznych.

W związku z tym równania racjonalne są równaniami o postaci :, gdzie - wyrażenia racjonalne.

Wcześniej rozważaliśmy tylko te racjonalne równania, które sprowadzają się do liniowych. Rozważmy teraz te racjonalne równania, które również można sprowadzić do równań kwadratowych.

Przykład 1

Rozwiązać równanie:.

Decyzja:

Ułamek jest równy 0 wtedy i tylko wtedy, gdy jego licznik wynosi 0, a mianownik nie jest równy 0.

Otrzymujemy następujący system:

Pierwsze równanie w systemie jest równaniem kwadratowym. Zanim go rozwiążemy, podzielmy wszystkie jego współczynniki przez 3. Otrzymamy:

Otrzymujemy dwa korzenie :; ...

Ponieważ 2 nigdy nie jest równe 0, konieczne jest spełnienie dwóch warunków: ... Ponieważ żaden z powyższych pierwiastków równania nie pokrywa się z niepoprawnymi wartościami zmiennej, które zostały uzyskane przez rozwiązanie drugiej nierówności, oba są rozwiązaniami tego równania.

Odpowiedź:.

Algorytm rozwiązywania racjonalnego równania

Sformułujmy więc algorytm rozwiązywania racjonalnych równań:

1. Przenieś wszystkie terminy na lewą stronę, aby uzyskać 0 po prawej stronie.

2. Przekształć i uprość lewą stronę, przenieś wszystkie ułamki do wspólnego mianownika.

3. Otrzymany ułamek jest równy 0, zgodnie z następującym algorytmem: .

4. Zapisz pierwiastki otrzymane w pierwszym równaniu i spełnij w odpowiedzi drugą nierówność.

Przykład rozwiązania racjonalnego równania

Weźmy inny przykład.

Przykład 2

Rozwiązać równanie: .

Decyzja

Na samym początku przenosimy wszystkie wyrazy na lewą stronę tak, aby po prawej pozostało 0. Otrzymujemy:

Teraz sprowadzamy lewą stronę równania do wspólnego mianownika:

To równanie jest równoważne z układem:

Pierwsze równanie w systemie jest równaniem kwadratowym.

Współczynniki tego równania: Obliczamy dyskryminatora:

Otrzymujemy dwa korzenie :; ...

Rozwiążmy teraz drugą nierówność: iloczyn czynników nie jest równy 0 wtedy i tylko wtedy, gdy żaden z czynników nie jest równy 0.

Konieczne jest spełnienie dwóch warunków: ... Otrzymujemy z dwóch pierwiastków pierwszego równania, tylko jedno pasuje - 3.

Nauczyliśmy się już rozwiązywać równania kwadratowe. Teraz rozszerzmy badane metody o równania racjonalne.

Co to jest racjonalna ekspresja? Napotkaliśmy już tę koncepcję. Wyrażenia racjonalne nazywane są wyrażenia złożone z liczb, zmiennych, ich stopni i znaków operacji matematycznych.

W związku z tym równania racjonalne są równaniami o postaci :, gdzie - wyrażenia racjonalne.

Wcześniej rozważaliśmy tylko te racjonalne równania, które sprowadzają się do liniowych. Rozważmy teraz te racjonalne równania, które również można sprowadzić do równań kwadratowych.

Przykład 1

Rozwiązać równanie:.

Decyzja:

Ułamek jest równy 0 wtedy i tylko wtedy, gdy jego licznik wynosi 0, a mianownik nie jest równy 0.

Otrzymujemy następujący system:

Pierwsze równanie w systemie jest równaniem kwadratowym. Zanim go rozwiążemy, podzielmy wszystkie jego współczynniki przez 3. Otrzymamy:

Otrzymujemy dwa korzenie :; ...

Ponieważ 2 nigdy nie jest równe 0, konieczne jest spełnienie dwóch warunków: ... Ponieważ żaden z powyższych pierwiastków równania nie pokrywa się z niepoprawnymi wartościami zmiennej, które zostały uzyskane przez rozwiązanie drugiej nierówności, oba są rozwiązaniami tego równania.

Odpowiedź:.

Sformułujmy więc algorytm rozwiązywania racjonalnych równań:

1. Przenieś wszystkie terminy na lewą stronę, aby uzyskać 0 po prawej stronie.

2. Przekształć i uprość lewą stronę, przenieś wszystkie ułamki do wspólnego mianownika.

3. Otrzymany ułamek jest równy 0, zgodnie z następującym algorytmem: .

4. Zapisz pierwiastki otrzymane w pierwszym równaniu i spełnij w odpowiedzi drugą nierówność.

Weźmy inny przykład.

Przykład 2

Rozwiązać równanie: .

Decyzja

Na samym początku przenosimy wszystkie wyrazy na lewą stronę tak, aby po prawej pozostało 0. Otrzymujemy:

Teraz sprowadzamy lewą stronę równania do wspólnego mianownika:

To równanie jest równoważne z układem:

Pierwsze równanie w systemie jest równaniem kwadratowym.

Współczynniki tego równania: Obliczamy dyskryminatora:

Otrzymujemy dwa korzenie :; ...

Rozwiążmy teraz drugą nierówność: iloczyn czynników nie jest równy 0 wtedy i tylko wtedy, gdy żaden z czynników nie jest równy 0.

Konieczne jest spełnienie dwóch warunków: ... Otrzymujemy z dwóch pierwiastków pierwszego równania, tylko jedno pasuje - 3.

Odpowiedź:.

Podczas tej lekcji przypomnieliśmy sobie, czym jest racjonalne wyrażenie, a także nauczyliśmy się, jak rozwiązywać racjonalne równania, które można sprowadzić do równań kwadratowych.

W następnej lekcji przyjrzymy się racjonalnym równaniom jako modelom rzeczywistych sytuacji, a także rozważymy problemy z ruchem.

Bibliografia

1. Bashmakov M.I. Algebra, klasa 8. - M.: Edukacja, 2004.
2. Dorofeev G.V., Suvorova S.B., Bunimovich E.A. i wsp. Algebra, 8. 5th ed. - M .: Edukacja, 2010.
3. Nikolsky S.M., Potapov M.A., Reshetnikov N.N., Shevkin A.V. Algebra, klasa 8. Podręcznik dla instytucji edukacyjnych. - M.: Edukacja, 2006.

1. Festiwal pomysłów pedagogicznych „Lekcja otwarta” ().
2. School.xvatit.com ().
3. Rudocs.exdat.com ().

Zadanie domowe

Algorytm rozwiązywania równań :

1. Rozwiń nawiasy.

)

Algorytm rozwiązywania równań :

1. Rozwiń nawiasy.

2. Zbierz wyrazy zawierające niewiadome po jednej stronie równania, a pozostałe wyrazy po drugiej. (przenosząc, zmień znak na przeciwny )

3. Wprowadź podobne wyrazy w każdej części równania.

4. Podzielić obie strony równania przez współczynnik nieznanego.

(Uwaga: często występują równania, dla których niektóre z tych kroków są niepotrzebne).

Algorytm rozwiązywania równań :

1. Rozwiń nawiasy.

2. Zbierz wyrazy zawierające niewiadome po jednej stronie równania, a pozostałe wyrazy po drugiej. (przenosząc, zmień znak na przeciwny )

3. Wprowadź podobne wyrazy w każdej części równania.

4. Podzielić obie strony równania przez współczynnik nieznanego.

(Uwaga: często występują równania, dla których niektóre z tych kroków są niepotrzebne).

Algorytm rozwiązywania równań :

1. Rozwiń nawiasy.

2. Zbierz wyrazy zawierające niewiadome po jednej stronie równania, a pozostałe wyrazy po drugiej. (przenosząc, zmień znak na przeciwny )

3. Wprowadź podobne wyrazy w każdej części równania.

4. Podzielić obie strony równania przez współczynnik nieznanego.

(Uwaga: często występują równania, dla których niektóre z tych kroków są niepotrzebne).

Algorytm rozwiązywania równań :

1. Rozwiń nawiasy.

2. Zbierz wyrazy zawierające niewiadome po jednej stronie równania, a pozostałe wyrazy po drugiej. (przenosząc, zmień znak na przeciwny )

3. Wprowadź podobne wyrazy w każdej części równania.

4. Podzielić obie strony równania przez współczynnik nieznanego.

(Uwaga: często występują równania, dla których niektóre z tych kroków są niepotrzebne).

Algorytm rozwiązywania równań :

1. Rozwiń nawiasy.

2. Zbierz wyrazy zawierające niewiadome po jednej stronie równania, a pozostałe wyrazy po drugiej. (przenosząc, zmień znak na przeciwny )

3. Wprowadź podobne wyrazy w każdej części równania.

4. Podzielić obie strony równania przez współczynnik nieznanego.

(Uwaga: często występują równania, dla których niektóre z tych kroków są niepotrzebne).

Algorytm rozwiązywania równań :

1. Rozwiń nawiasy.

2. Zbierz wyrazy zawierające niewiadome po jednej stronie równania, a pozostałe wyrazy po drugiej. (przenosząc, zmień znak na przeciwny )

3. Wprowadź podobne wyrazy w każdej części równania.

4. Podzielić obie strony równania przez współczynnik nieznanego.

(Uwaga: często występują równania, dla których niektóre z tych kroków są niepotrzebne).

Algorytm rozwiązywania równań :

1. Rozwiń nawiasy.

2. Zbierz wyrazy zawierające niewiadome po jednej stronie równania, a pozostałe wyrazy po drugiej. (przenosząc, zmień znak na przeciwny )

3. Wprowadź podobne wyrazy w każdej części równania.

4. Podzielić obie strony równania przez współczynnik nieznanego.

(Uwaga: często występują równania, dla których niektóre z tych kroków są niepotrzebne).