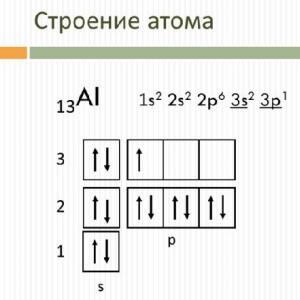
Koji se brojevni nizovi nazivaju monotonima. Brojne sekvence

Ako je svaki prirodni broj n povezan s nekim stvarnim brojem x n, tada kažu da je dat numerički slijed

x 1 , x 2 , … x n , …

Broj x 1 naziva se članom niza sa brojem 1 ili prvi pojam u nizu, broj x 2 - član niza sa brojem 2 ili drugi član niza itd. Poziva se broj x n član niza numerirann.

Postoje dva načina za određivanje sekvenci brojeva - sa i sa ponavljajuća formula.

Sekvenciranje sa formule uobičajenih termina Je zadatak u nizu

x 1 , x 2 , … x n , …

koristeći formulu koja izražava zavisnost pojma x n od njegovog broja n.

Primjer 1. Redoslijed brojeva

1, 4, 9, … n 2 , …

dato zajedničkom formulom izraza

x n = n 2 , n = 1, 2, 3, …

Sekvenciranje pomoću formule koja izražava člana sekvence x n u terminima članova sekvence s prethodnim brojevima naziva se sekvenciranje pomoću ponavljajuća formula.

x 1 , x 2 , … x n , …

zove sve veća sekvenca, više prethodni član.

Drugim riječima, za sve n

x n + 1 > x n

Primjer 3. Slijed prirodnih brojeva

1, 2, 3, … n, …

je sve veća sekvenca.

Definicija 2. Redoslijed brojeva

x 1 , x 2 , … x n , …

zove opadajući redoslijed, ako svaki član ove sekvence manje prethodni član.

Drugim riječima, za sve n \u003d 1, 2, 3, ... nejednakost

x n + 1 < x n

Primjer 4. Slijed

dato formulom

je silazni niz.

Primjer 5. Redoslijed brojeva

1, - 1, 1, - 1, …

dato formulom

x n = (- 1) n , n = 1, 2, 3, …

nije niti se povećava niti smanjuje slijed.

Definicija 3. Pozivaju se povećavajući i smanjujući numerički nizovi monotoni nizovi.

Ograničene i neograničene sekvence

Definicija 4. Redoslijed brojeva

x 1 , x 2 , … x n , …

zove omeđena odozgo, ako postoji broj M takav da svaki član ove sekvence manje brojevi M.

Drugim riječima, za sve n \u003d 1, 2, 3, ... nejednakost

Definicija 5. Numerički slijed

x 1 , x 2 , … x n , …

zove ograničeno odozdo, ako postoji broj m takav da svaki član ove sekvence više brojevi m.

Drugim riječima, za sve n \u003d 1, 2, 3, ... nejednakost

Definicija 6. Redoslijed brojeva

x 1 , x 2 , … x n , …

naziva se ograničenim ako je omeđena i gore i dolje.

Drugim riječima, postoje brojevi M i m takvi da su za sve n \u003d 1, 2, 3, ... nejednakost

m< x n < M

Definicija 7. Numeričke sekvence koje nisu ograničenisu pozvani neograničene sekvence.

Primjer 6. Redoslijed brojeva

1, 4, 9, … n 2 , …

dato formulom

x n = n 2 , n = 1, 2, 3, … ,

omeđena odozdo, na primjer, broj 0. Međutim, ovaj niz neograničeno odozgo.

Primjer 7. Slijed

dato formulom

je ograničena sekvencajer za sve n \u003d 1, 2, 3, ... nejednakost

Na našoj veb stranici takođe se možete upoznati sa materijalima za obuku koji su razvili nastavnici Resolvent centra za obuku za pripremu za Jedinstveni državni ispit i OGE iz matematike.

Za školarce koji se žele dobro pripremiti i proći Jedinstveni državni ispit iz matematike ili ruskog jezika za visoku ocjenu provodi Resolvent trening centar

pripremni tečajevi za školarce 10. i 11. razreda

Definicija 1. Niz se naziva nemanjujućim [nerastućim] ako svaki element niza, počevši od drugog, nije manji (ne više od) svog prethodnog elementa, odnosno ako je nejednakost

Definicija 2. Niz se naziva monoton ako se ne smanjuje ili ne povećava.

Ako elementi ne-padajućeg niza za sve brojeve zadovoljavaju strogu nejednakost, tada se taj niz naziva povećanjem.

Slično tome, ako elementi nerastućeg niza za sve brojeve zadovoljavaju strogu nejednakost, tada se taj niz naziva opadajući.

Imajte na umu da je bilo koja monotona sekvenca očigledno ograničena na jednoj strani (bilo iznad ili ispod). Zapravo, bilo koja se ne smanjujuća sekvenca ograničena je odozdo (vrijednost njenog prvog elementa može se uzeti kao donja granica), a bilo koja nerastuća sekvenca ograničena je odozgo (vrijednost njegovog prvog elementa može se uzeti i kao gornja granica).

Iz toga slijedi da će nenasiruća sekvenca biti ograničena s obje strane, ili jednostavno ograničena ako i samo ako je ograničena odozgo, a nerastuća sekvenca bit će ograničena onda i samo ako je ograničena odozdo.

Razmotrimo primjere monotonih sekvenci.

1. Redoslijed se ne smanjuje. Odozdo je ograničen vrijednošću svog prvog elementa, ali nije ograničen odozgo.

2. Niz se smanjuje. Ograničen je s obje strane: na vrhu vrijednošću svog prvog elementa 2, a na dnu, na primjer, brojem 1.

Definicija1. Poziva se niz opadajući (ne-povećanje ) ako za sve
vrijedi nejednakost
.

Definicija2. Slijed
zove raste (ne smanjuje se ) ako za sve
vrijedi nejednakost
.

Definicija3. Pozvani su opadajući, nerastući, rastući i ne smanjujući se nizovi monotono sekvence, se smanjuju i povećavaju sekvence strogo monotono sekvence.

Očigledno je da se ne-smanjujući niz ograničava odozdo, a ne-sekvencijski odozdo. Stoga je svaki monotoni slijed očito ograničen s jedne strane.

Primjer1. Slijed
povećava, ne smanjuje,
opada
se ne povećava
- ne-monoton niz.

Za monotone sekvence, sljedeću ulogu igra važna uloga.

Teorem1. Ako je ne-opadajući (ne-uvećavajući) niz ograničen gore (dolje), tada konvergira.

Dokazi... Neka slijed
ne smanjuje se i ograničen je odozgo, tj.
i mnogi
omeđena odozgo. Prema teoremu 1 § 2, postoji
... Dokažimo to
.

Uzmimo
proizvoljno. Zbog i- tačna gornja granica, broj postoji N takav da
... Budući da se niz ne smanjuje, onda za sve
imamo, tj.
, tako
za sve
, a to znači da
.

Za nerastuću sekvencu ograničenu odozdo, dokaz je sličan ( studenti mogu sami to dokazati kod kuće). Teorem je dokazan.

Komentar... Teorem 1 se može drugačije formulirati.

Teorem2. Da bi se monotoni niz konvergirao, potrebno je i dovoljno da bude ograničen.

Dovoljnost je utvrđena u teoremu 1, a nužnost - u teoremi 2 § 5.

Uvjet monotonosti nije potreban da bi se niz konvergirao, jer konvergentni niz nije nužno monoton. Na primjer, slijed
nije monotono, već konvergira na nulu.

Posljedica... Ako slijed
tada se povećava (smanjuje) i ograničava iznad (dolje)
(
).

Zaista, prema teoremu 1
(
).

Definicija4. Ako i
u
, tada se poziva sekvenca sistem ugovaranja ugniježđenih segmenata linija .

Teorem3 (princip ugniježđenih segmenata linija). Bilo koji sustav ugovaranja ugniježđenih segmenata ima i, osim toga, jedinstvenu točku odkoji pripadaju svim segmentima ovog sistema.

Dokazi... Dokažimo to odpostoji. Zbog
onda
a samim tim i slijed
se ne smanjuje, već redoslijed
se ne povećava. U čemu
i
ograničen od. Tada, prema teoremu 1, postoje
i
, ali od tada
onda
=
... Pronađena tačka odpripada svim segmentima sistema, budući da je posljedicom teorema 1
,
, tj.
za sve vrijednosti n.

Pokažimo sada to od- jedini. Pretpostavimo da postoje dvije takve točke: odi di neka za određenost
... Zatim segment
pripada svim segmentima
, tj.
za sve n, što je nemoguće, budući da
i, dakle, počevši od nekog broja,
... Teorem je dokazan.

Imajte na umu da je ovdje bitno da uzmemo u obzir zatvorene intervale, tj. segmenti. Ako uzmemo u obzir sistem ugovaranja intervala, princip je, uopšteno govoreći, netačan. Na primjer intervali
očigledno ugovor do te mjere
ali poenta
ne pripada nijednom intervalu ovog sistema.

Razmotrimo sada primjere konvergentnih monotonih sekvenci.

1) Broj e.

Razmislite sada o redoslijedu
... Kako se ona ponaša? Baza

stupanj
, tako
? S druge strane,
, i
, tako
? Ili nema ograničenja?

Da biste odgovorili na ova pitanja, razmotrite pomoćni niz
... Dokažimo da se smanjuje i ograničava odozdo. U ovom slučaju trebat ćemo

Lemma... Ako
, zatim za sve prirodne vrijednosti nimamo

(Bernoullijeva nejednakost).

Dokazi... Koristimo metodu matematičke indukcije.

Ako
onda
, tj. nejednakost je istinita.

Pretpostavimo da je to tačno za
i dokazati njegovu valjanost za
+1.

Tačno
... Množimo ovu nejednakost sa
:

Na ovaj način, . Dakle, prema principu matematičke indukcije, Bernoullijeva nejednakost vrijedi za sve prirodne vrijednosti n... Lema je dokazana.

Pokažimo taj niz
opada. Imamo

\u200c\u200c\u200c׀ Bernoullijeva nejednakost ׀
, što znači da je niz
opada.

Ograničenost odozdo slijedi iz nejednakosti
\u200c\u200c\u200c׀ Bernoullijeva nejednakost ׀
za sve prirodne vrijednosti n.

Prema teoremu 1, postoji
, što je označeno slovom e... dakle
.

Broj eiracionalno i transcendentalno, e\u003d 2.718281828 .... Poznato je da je osnova prirodnih logaritama.

Primjedbe... 1) Bernoullijeva nejednakost može se koristiti da se to dokaže
u
... Zaista, ako
onda
... Zatim, Bernoullijevom nejednakošću, za
... Dakle, na
imamo
, tj
u
.

2) U gornjem primjeru, osnova stepena teži 1, a eksponent n- do , odnosno postoji neizvjesnost oblika ... Nesigurnost ove vrste, kao što smo pokazali, otkriva se uz pomoć izuzetne granice
.

2)
(*)

Dokažimo da se ovaj niz konvergira. Da bismo to učinili, pokazat ćemo da je ograničeno odozdo i da se ne povećava. U ovom slučaju koristimo nejednakost
za sve
, što je posljedica nejednakosti
.

Imamo
cm. nejednakost iznad
, tj. niz je dolje ograničen brojem
.

Dalje,
 od

, tj. sekvenca se ne povećava.

Prema teoremu 1, postoji
, koju označavamo x... Prelazak u jednakost (*) do granice na
, dobijamo

, tj.
odakle
(uzimamo znak plus, jer su svi članovi niza pozitivni).

Za izračunavanje se koristi sekvenca (*)
otprilike. Per uzmi bilo koji pozitivan broj. Na primjer, pronađimo
... Neka bude
... Onda
,. Na ovaj način,
.

3)
.

Imamo
... Zbog
u
, postoji broj N, takav da je za sve
vrijedi nejednakost
... Dakle, slijed
počevši od nekog broja N, smanjuje se i ograničava se odozdo, budući da
za sve vrijednosti n... Dakle, prema teoremu 1 postoji
... Zbog
, imamo
.

Dakle,
.

4)
, zdesna - n korijenje.

Pokažimo matematičkom indukcijom da
za sve vrijednosti n... Imamo
... Neka bude
... Zatim, odavde dobivamo izjavu po principu matematičke indukcije. Koristeći ovu činjenicu, nalazimo, tj. slijed
povećava se i ograničena je odozgo. Stoga postoji od
.

Na ovaj način,
.

Weierstrassov teorem o granici monotonog niza

Bilo koja monotona ograničena sekvenca (x n) ima konačnu granicu jednaku tačnoj gornjoj granici, sup (x n) za opadajuću i tačnu donju granicu, inf (x n) za nerastuću sekvencu.
Bilo koja monotona neograničena sekvenca ima beskonačnu granicu jednaku plus beskonačnosti za ne smanjujući i minus beskonačnosti za nerastuću sekvencu.

Dokazi

1) ne-opadajuća ograničena sekvenca.

(1.1) .

Budući da je niz ograničen, on ima konačnu tačno gornju granicu
.
To znači da:

• za sve n,
  (1.2) ;
• za bilo koji pozitivan broj postoji takav broj ovisno o ε, tako da
  (1.3) .

.
Ovdje smo također koristili (1.3). Kombinirajući sa (1.2), nalazimo:
u.
Od tada
,
ili
u.
Dokazan je prvi dio teorema.

2) Sad neka bude slijed nerastuća ograničena sekvenca:
(2.1) za sve n.

Budući da je niz ograničen, on ima konačnu tačno donju granicu
.
To znači sljedeće:

• za sve n vrijede sljedeće nejednakosti:
  (2.2) ;
• za bilo koji pozitivan broj postoji broj koji ovisi o ε za koji
  (2.3) .

.
Ovdje smo također koristili (2.3). Uzimajući u obzir (2.2), nalazimo:
u.
Od tada
,
ili
u.
To znači da je broj ograničenje niza.
Dokazan je drugi dio teorema.

Sada razmotrimo neograničene sekvence.
3) Neka slijed bude neograničeni niz koji se ne smanjuje.

Budući da se niz ne smanjuje, za sve n vrijede sljedeće nejednakosti:
(3.1) .

Budući da se niz ne smanjuje i ne ograničava, on je neograničen na desnoj strani. Tada za bilo koji broj M postoji broj koji ovisi o M za koji
(3.2) .

Budući da se niz ne smanjuje, tada za:
.
Ovdje smo također koristili (3.2).

.
To znači da je ograničenje niza plus beskonačnost:
.
Treći dio teorema je dokazan.

4) Na kraju, razmotrite slučaj kada jeste neograničena nerastuća sekvenca.

Slično prethodnom, s obzirom da se niz ne povećava
(4.1) za sve n.

Budući da se niz ne povećava i ne ograničava, on je neograničen na lijevoj strani. Tada za bilo koji broj M postoji broj, ovisno o M za koji
(4.2) .

Budući da se sekvenca ne povećava, tada imamo:
.

Dakle, za bilo koji broj M postoji prirodni broj koji ovisi o M, tako da za sve brojeve vrijede sljedeće nejednakosti:
.
To znači da je ograničenje niza minus beskonačnost:
.
Teorem je dokazan.

Primjer rješavanja problema

Koristeći Weierstrassovu teoremu dokažite konvergenciju niza:
, , . . . , , . . .
Zatim pronađite njegovu granicu.

Predstavimo niz u obliku ponavljajućih formula:
,
.

Dokažimo da je zadati niz odozgo ograničen vrijednošću
(W1) .
Dokaz provodimo metodom matematičke indukcije.
.
Neka bude. Onda
.
Dokazana je nejednakost (A1).

Dokažimo da se niz monotono povećava.
;
(P2) .
Budući da su nazivnik razlomka i prvi faktor u brojniku pozitivni. Zbog ograničenosti članova niza nejednakošću (A1), drugi faktor je takođe pozitivan. dakle
.
Odnosno, slijed se strogo povećava.

Budući da se sekvenca povećava i ograničava odozgo, to je ograničena sekvenca. Prema tome, prema Weierstrassovom teoremu, on ima ograničenje.

Pronađimo ovo ograničenje. Označimo to sa:
.
Koristit ćemo činjenicu da
.
Primjenjujemo ovo na (A2) koristeći aritmetička svojstva ograničenja konvergentnih sekvenci:
.
Korijen zadovoljava uvjet.