Zapiski predavanj iz mehanike. Tehnična mehanika
1 diapozitiv
Tečaj predavanj teoretična mehanika Dinamika (I del) Bondarenko A.N. Moskva - 2007 Elektronski tečaj usposabljanja je bil napisan na podlagi avtorjevih predavanj za študente, ki študirajo na specialnostih SZhD, PGS in SDM na NIIZhT in MIIT (1974-2006). Učno gradivo ustreza koledarskim načrtom v obsegu treh semestrov. Za popolno implementacijo animacijskih učinkov med predstavitvijo morate uporabiti pregledovalnik Power Point, ki ni nižji od tistega, ki je vgrajen v Microsoft Office operacijskega sistema Windows-XP Professional. Pripombe in predloge lahko pošljete po e-pošti: [email protected]. Moskva Državna univerzaŽeleznice (MIIT) Oddelek za teoretično mehaniko Znanstveno-tehnični center za prometne tehnologije

2 diapozitiv
Vsebina Predavanje 1. Uvod v dinamiko. Zakoni in aksiomi dinamike materialnih točk. Osnovna enačba dinamike. Diferencialne in naravne enačbe gibanja. Dve glavni nalogi dinamike. Primeri reševanja neposrednega problema dinamike Predavanje 2. Reševanje inverznega problema dinamike. Splošna navodila za reševanje inverznega problema dinamike. Primeri reševanja inverznega problema dinamike. Gibanje telesa, vrženega pod kotom proti obzorju, brez upoštevanja zračnega upora. Predavanje 3. Premočrtna nihanja materialne točke. Pogoj za nastanek nihanj. Razvrstitev vibracij. Proste vibracije brez upoštevanja upornih sil. dušene vibracije. Zmanjšanje nihanja. Predavanje 4. Prisilna nihanja materialne točke. Resonanca. Vpliv upora proti gibanju pri prisilnih vibracijah. Predavanje 5. Relativno gibanje materialne točke. Sile vztrajnosti. Posebni primeri gibanja za različne vrste prenosnih premikov. Vpliv vrtenja Zemlje na ravnovesje in gibanje teles. Predavanje 6. Dinamika mehanskega sistema. mehanski sistem. Zunanje in notranje sile. Masno središče sistema. Izrek o gibanju središča mase. Ohranjevalni zakoni. Primer reševanja problema uporabe izreka o gibanju središča mase. Predavanje 7. Impulz sile. Količina gibanja. Izrek o spremembi zagona. Ohranjevalni zakoni. Eulerjev izrek. Primer reševanja problema o uporabi izreka o spremembi gibalne količine. moment zagona. Izrek o spreminjanju kotne količine Predavanje 8. Ohranjevalni zakoni. Elementi teorije vztrajnostnih momentov. Kinetični moment togega telesa. Diferencialna enačba vrtenja togega telesa. Primer reševanja problema uporabe izreka o spreminjanju kotnega momenta sistema. Osnovna teorija žiroskopa. Priporočena literatura 1. Yablonsky A.A. Tečaj teoretične mehanike. 2. del. M.: Višja šola. 1977. 368 str. 2. Meshchersky I.V. Zbirka problemov iz teoretične mehanike. M.: Znanost. 1986 416 str. 3. Zbirka nalog za seminarske naloge/ Ed. A.A. Yablonski. M.: Višja šola. 1985. 366 str. 4. Bondarenko A.N. »Teoretična mehanika v primerih in nalogah. Dynamics" (elektronski priročnik www.miit.ru/institut/ipss/faculties/trm/main.htm), 2004

3 diapozitiv
Predavanje 1 Dinamika je del teoretične mehanike, ki preučuje mehansko gibanje z najbolj splošnega vidika. Gibanje se obravnava v povezavi s silami, ki delujejo na predmet. Sekcija je sestavljena iz treh sklopov: Dinamika materialne točke Dinamika mehanskega sistema Analitična mehanika ■ Dinamika točke - preučuje gibanje materialne točke ob upoštevanju sil, ki to gibanje povzročajo. Glavni predmet je materialna točka - materialno telo z maso, katere dimenzije lahko zanemarimo. Osnovne predpostavke: - obstaja absolutni prostor (ima čisto geometrijske lastnosti, ki niso odvisne od snovi in njenega gibanja. - obstaja absolutni čas (ni odvisen od materije in njenega gibanja). Iz tega sledi: - obstaja absolutno nepremičen referenčni okvir - čas ni odvisen od gibanja referenčnega okvira - mase gibljivih točk niso odvisne od gibanja referenčnega okvira. Te predpostavke se uporabljajo v klasični mehaniki, ki sta jo ustvarila Galileo in Newton Še vedno ima dokaj širok obseg, saj mehanski sistemi, ki jih obravnavajo uporabne znanosti, nimajo tako velikih mas in hitrosti gibanja, za kar je treba upoštevati njihov vpliv na geometrijo prostora, časa, gibanja, kot npr. se izvaja v relativistični mehaniki (teoriji relativnosti) ■ Osnovni zakoni dinamike - prvi odkril Galileo in oblikoval Newton, so osnova za vse metode za opis in analizo gibanja mehanskih sistemov in njihove dinamične interakcije. delovanje pod vplivom različnih sil. ■ Zakon vztrajnosti (Galileo-Newtonov zakon) - Izolirana materialna točka telesa ohranja stanje mirovanja ali enakomernega pravokotnega gibanja, dokler ga uporabljene sile ne prisilijo, da to stanje spremeni. To pomeni enakovrednost stanja mirovanja in gibanja po vztrajnosti (Galilejev zakon relativnosti). Referenčni okvir, v zvezi s katerim je izpolnjen zakon vztrajnosti, se imenuje inercialni. Lastnost materialne točke, da si prizadeva ohraniti hitrost svojega gibanja (svoje kinematično stanje) nespremenjeno, se imenuje vztrajnost. ■ Zakon sorazmernosti sile in pospeška (Osnovna enačba dinamike - Newtonov II zakon) - Pospešek, ki se materialni točki prenese s silo, je neposredno sorazmeren s silo in obratno sorazmeren z maso te točke: ali Tukaj je m masa točke (merila vztrajnosti), merjena v kg, številčno enaka teži, deljeni z gravitacijskim pospeškom: F je delujoča sila, merjena v N (1 N daje pospešek 1 m / s2 točki mase 1 kg, 1 N \u003d 1/9. 81 kg-s). ■ Dinamika mehanskega sistema - preučuje gibanje niza materialnih točk in trdnih teles, združenih s splošnimi zakoni interakcije, ob upoštevanju sil, ki to gibanje povzročajo. ■ Analitična mehanika - preučuje gibanje neprostih mehanskih sistemov z uporabo splošnih analitskih metod. eno

4 diapozitiv
Predavanje 1 (nadaljevanje - 1.2) Diferencialne enačbe gibanja materialne točke: - diferencialna enačba gibanja točke v vektorski obliki. - diferencialne enačbe gibanja točke v koordinatni obliki. Ta rezultat je mogoče dobiti s formalno projekcijo vektorske diferencialne enačbe (1). Po združevanju se vektorska relacija razstavi v tri skalarne enačbe: V koordinatni obliki: Uporabimo razmerje polmera-vektorja s koordinatami in vektorja sile s projekcijami: diferencialna enačba gibanja na naravnih (premičnih) koordinatnih osi: ali: - naravne enačbe gibanja točke. ■ Osnovna enačba dinamike: - ustreza vektorskemu načinu podajanja gibanja točke. ■ Zakon neodvisnosti delovanja sil - Pospešek materialne točke pod delovanjem več sil je enak geometrijski vsoti pospeškov točke od delovanja vsake od sil posebej: ali Velja zakon. za katero koli kinematsko stanje teles. Sile interakcije, ki delujejo na različne točke (telesa), niso uravnotežene. ■ Zakon enakosti delovanja in reakcije (Newtonov III zakon) - Vsakemu dejanju ustreza enaka in nasprotno usmerjena reakcija: 2

5 diapozitiv
Dva glavna problema dinamike: 1. Neposredni problem: Gibanje je podano (enačbe gibanja, trajektorija). Potrebno je določiti sile, pod katerimi se določeno gibanje pojavi. 2. Inverzni problem: Podane so sile, pod vplivom katerih pride do gibanja. Potrebno je najti parametre gibanja (enačbe gibanja, trajektorijo gibanja). Oba problema sta rešena z uporabo osnovne enačbe dinamike in njene projekcije na koordinatne osi. Če upoštevamo gibanje neproste točke, se tako kot v statiki uporablja načelo sprostitve iz vezi. Kot rezultat reakcije so vezi vključene v sestavo sil, ki delujejo na materialno točko. Rešitev prvega problema je povezana z diferenciacijskimi operacijami. Rešitev inverznega problema zahteva integracijo ustreznih diferencialnih enačb, kar je veliko težje kot diferenciacija. Inverzni problem je težji od neposrednega problema. Rešitev neposrednega problema dinamike - poglejmo primere: Primer 1. Kabino s težo G dvigala dvigne kabel s pospeškom a . Določite napetost kabla. 1. Izberite predmet (kabina dvigala se premika naprej in se lahko obravnava kot materialna točka). 2. Priključek (kabel) zavržemo in ga nadomestimo z reakcijo R. 3. Sestavimo osnovno enačbo dinamike: Določimo reakcijo kabla: Določimo napetost kabla: Z enakomernim gibanjem kabine ay = 0 in napetost kabla je enaka teži: T = G. Ko se kabel pretrga T = 0 in je pospešek kabine enak pospešku prostega pada: ay = -g. 3 4. Osnovno enačbo dinamike projiciramo na os y: y Primer 2. Točka mase m se giblje vzdolž vodoravne površine (ravnina Oxy) po enačbah: x = a coskt, y = b coskt. Določite silo, ki deluje na točko. 1. Izberite predmet (materialno točko). 2. Povezavo (ravnino) zavržemo in jo nadomestimo z reakcijo N. 3. Sistemu sil dodamo neznano silo F. 4. Sestavimo osnovno enačbo dinamike: 5. Osnovno enačbo dinamike projiciramo na x , y osi: Določite projekcije sile: Modul sile: Smerni kosinus : Tako je velikost sile sorazmerna z razdaljo točke do središča koordinat in je usmerjena proti središču vzdolž premice, ki povezuje točko s središčem . Pot gibanja točke je elipsa s središčem v izhodišču: O r Predavanje 1 (nadaljevanje - 1.3)

6 diapozitiv
1. predavanje (nadaljevanje 1.4) Primer 3: Tovor z utežjo G je obešen na vrvi dolžine l in se giblje po krožni poti v vodoravni ravnini z določeno hitrostjo. Kot odstopanja kabla od navpičnice je enak. Določite napetost kabla in hitrost bremena. 1. Izberite predmet (tovor). 2. Zavrzite povezavo (vrv) in jo zamenjajte z reakcijo R. 3. Sestavite glavno enačbo dinamike: Iz tretje enačbe določite reakcijo kabla: Določite napetost kabla: Nadomestite vrednost reakcije kabla, normalni pospešek v drugo enačbo in določimo hitrost obremenitve: 4. Projiciraj glavno enačbo osno dinamiko,n,b: Primer 4: Avtomobil teže G se giblje po konveksnem mostu (polmer ukrivljenosti je R ) s hitrostjo V. Določi pritisk avtomobila na most. 1. Izberemo predmet (avto, dimenzije zanemarimo in ga obravnavamo kot točko). 2. Povezavo (hrapava površina) zavržemo in jo nadomestimo z reakcijama N in torno silo Ffr. 3. Sestavimo osnovno enačbo dinamike: 4. Osnovno enačbo dinamike projiciramo na os n: Od tu določimo normalno reakcijo: Določimo tlak avtomobila na mostu: Od tu lahko določimo hitrost ustreza ničelnemu tlaku na mostu (Q = 0): 4

7 diapozitiv
Predavanje 2 Po zamenjavi najdenih vrednosti konstant dobimo: Tako lahko materialna točka pod delovanjem istega sistema sil izvede cel razred premikov, določenih z začetnimi pogoji. Začetne koordinate upoštevajo začetni položaj točke. Začetna hitrost, podana s projekcijami, upošteva vpliv na njeno gibanje vzdolž obravnavanega odseka poti sil, ki so delovale na točko pred prihodom na ta odsek, t.j. začetno kinematično stanje. Rešitev inverznega problema dinamike - V splošnem primeru gibanja točke so sile, ki delujejo na točko, spremenljivke, ki so odvisne od časa, koordinat in hitrosti. Gibanje točke je opisano s sistemom treh diferencialnih enačb drugega reda: Po integraciji vsake od njih bo šest konstant C1, C2,…., C6: vrednosti konstant C1, C2,… ., C6 najdemo iz šestih začetnih pogojev pri t = 0: Primer 1 rešitve inverznega problema: Prosta materialna točka mase m se premika pod delovanjem sile F, ki je konstantna po velikosti in velikosti. . V začetnem trenutku je bila hitrost točke v0 in je sovpadala v smeri s silo. Določi enačbo gibanja točke. 1. Sestavimo osnovno enačbo dinamike: 3. Znižamo vrstni red izpeljanke: 2. Izberemo kartezinski referenčni sistem, ki usmerimo os x vzdolž smeri sile in na to os projiciramo glavno enačbo dinamike: ali xyz 4. Loči spremenljivke: 5. Izračunaj integrale iz obeh delov enačbe : 6. Predstavimo projekcijo hitrosti kot časovno izpeljanko koordinate: 8. Izračunaj integrale obeh delov enačbe: 7. Ločimo spremenljivke: 9. Za določitev vrednosti konstant C1 in C2 uporabimo začetne pogoje t = 0, vx = v0 , x = x0: Kot rezultat dobimo enačbo enakomerno spremenljivega gibanja (vzdolž os x): 5

8 diapozitiv
Splošna navodila za reševanje neposrednih in inverznih nalog. Postopek rešitve: 1. Sestavljanje diferencialne enačbe gibanja: 1.1. Izberite koordinatni sistem - pravokoten (fiksen) z neznano potjo gibanja, naravni (gibljiv) z znano potjo, na primer krog ali ravna črta. V slednjem primeru se lahko uporabi ena premočrtna koordinata. Referenčno točko je treba kombinirati z začetnim položajem točke (pri t = 0) ali z ravnotežnim položajem točke, če obstaja, na primer, ko točka niha. 6 1.2. Nariši točko na položaju, ki ustreza poljubnemu trenutku v času (za t > 0), tako da so koordinate pozitivne (s > 0, x > 0). Predvidevamo tudi, da je tudi projekcija hitrosti v tem položaju pozitivna. V primeru nihanja projekcija hitrosti spremeni predznak, na primer ob vrnitvi v ravnotežni položaj. Pri tem je treba domnevati, da se v obravnavanem trenutku točka odmakne od ravnotežnega položaja. Izvajanje tega priporočila je pomembno v prihodnosti pri delu z upornimi silami, ki so odvisne od hitrosti. 1.3. Osvobodite materialno točko vezi, njihovo delovanje nadomestite z reakcijami, dodajte aktivne sile. 1.4. Zapišite osnovni zakon dinamike v vektorski obliki, projicirate na izbrane osi, izrazite dane ali reaktivne sile s časovnimi, koordinatnimi ali hitrostnimi spremenljivkami, če so od njih odvisne. 2. Rešitev diferencialnih enačb: 2.1. Zmanjšajte izvod, če enačba ni reducirana na kanonično (standardno) obliko. na primer: ali 2.2. Ločene spremenljivke, na primer: ali 2.4. Izračunaj nedoločene integrale na levi in desni strani enačbe, na primer: 2.3. Če so v enačbi tri spremenljivke, spremenite spremenljivke, na primer: in nato ločite spremenljivke. Komentar. Namesto vrednotenja nedoločenih integralov lahko ovrednotimo določene integrale s spremenljivo zgornjo mejo. Spodnje meje predstavljajo začetne vrednosti spremenljivke (začetni pogoji) Potem ni treba posebej iskati konstante, ki se samodejno vključi v rešitev, na primer: Z uporabo začetnih pogojev, na primer t = 0, vx = vx0, določimo konstanto integracije: 2.5. Hitrost izrazite na primer s časovno izpeljavo koordinate in ponovite korake 2.2 -2.4 Opomba. Če se enačba zmanjša na kanonično obliko, ki ima standardno rešitev, se uporabi ta že pripravljena rešitev. Konstante integracije še vedno najdemo iz začetnih pogojev. Glej na primer nihanja (predavanje 4, str. 8). 2. predavanje (nadaljevanje 2.2)

9 diapozitiv
2. predavanje (nadaljevanje 2.3) 2. primer reševanja inverznega problema: Sila je odvisna od časa. Tovor z utežjo P se začne premikati po gladki vodoravni površini pod delovanjem sile F, katere velikost je sorazmerna s časom (F = kt). Določite razdaljo, ki jo je tovor prevozil v času t. 3. Sestavite osnovno enačbo dinamike: 5. Zmanjšajte vrstni red izpeljanke: 4. Osnovno enačbo dinamike projicirate na os x: ali 7 6. Ločite spremenljivke: 7. Izračunajte integrale obeh delov enačba: 9. Predstavite projekcijo hitrosti kot izvod koordinate glede na čas: 10. Izračunajte integrale obeh delov enačbe: 9. Ločite spremenljivke: 8. Določite vrednost konstante C1 iz začetni pogoj t = 0, vx = v0=0: Kot rezultat dobimo enačbo gibanja (vzdolž osi x), ki poda vrednost prevožene razdalje za čas t: 1. Izberemo referenčni sistem (kartezijanski koordinate), tako da ima telo pozitivno koordinato: 2. Predmet gibanja vzamemo kot materialno točko (telo se premika naprej), ga sprostimo iz povezave (referenčne ravnine) in nadomestimo z reakcijo (normalna reakcija gladka površina) : 11. Določi vrednost konstante C2 iz začetnega pogoja t = 0, x = x0=0: 3. primer reševanja inverzne naloge: Sila je odvisna od koordinate. Materialna točka mase m se vrže z zemeljskega površja navzgor s hitrostjo v0. Sila težnosti Zemlje je obratno sorazmerna s kvadratom razdalje od točke do težišča (središče Zemlje). Določi odvisnost hitrosti od razdalje y do središča Zemlje. 1. Referenčni sistem (kartezijanske koordinate) izberemo tako, da ima telo pozitivno koordinato: 2. Sestavimo osnovno enačbo dinamike: 3. Osnovno enačbo dinamike projiciramo na os y: ali Koeficient sorazmernosti lahko najdemo s pomočjo teže točke na zemeljskem površju: R Zato je diferencial enačbe videti tako: ali 4. Zmanjšaj vrstni red odvoda: 5. Spremeni spremenljivko: 6. Loči spremenljivke: 7. Izračunaj integralov obeh strani enačbe: 8. Zamenjaj meje: Kot rezultat dobimo izraz za hitrost kot funkcijo koordinate y: Največjo višino leta lahko najdemo tako, da hitrost enačimo z nič: Največja višina leta ko se imenovalec obrne na nič: Od tu se pri nastavitvi polmera Zemlje in pospeška prostega pada dobi II kozmična hitrost:

10 diapozitiv
2. predavanje (nadaljevanje 2.4) 2. primer reševanja inverzne naloge: Sila je odvisna od hitrosti. Ladja mase m je imela hitrost v0. Odpor vode proti gibanju ladje je sorazmeren s hitrostjo. Določite čas, v katerem se hitrost ladje po izklopu motorja zmanjša za polovico, ter razdaljo, ki jo je ladja prepotovala do popolne ustavitve. 8 1. Izberemo referenčni sistem (kartezijeve koordinate), tako da ima telo pozitivno koordinato: 2. Predmet gibanja vzamemo kot materialno točko (ladja se premika naprej), ga osvobodimo vezi (vode) in zamenjamo. z reakcijo (vzgona - Arhimedova sila), pa tudi silo upora proti gibanju. 3. Dodajte aktivno silo (gravitacijo). 4. Sestavimo glavno enačbo dinamike: 5. Glavno enačbo dinamike projiciramo na os x: ali 6. Spustimo vrstni red izpeljanke: 7. Ločimo spremenljivke: 8. Izračunamo integrale iz obeh deli enačbe: 9. Zamenjamo meje: Dobimo izraz, ki povezuje hitrost in čas t, iz katerega lahko določimo čas gibanja: Čas gibanja, med katerim bo hitrost padla za polovico: Je zanimivo je, da ko se hitrost približa nič, čas gibanja teži k neskončnosti, tj končna hitrost ne more biti nič. Zakaj ne "perpetual motion"? Vendar je v tem primeru prevožena razdalja do postajališča končna vrednost. Za določitev prevožene razdalje se obrnemo na izraz, ki ga dobimo po znižanju vrstnega reda odvoda, in spremenimo spremenljivko: Po integraciji in zamenjavi mej dobimo: Prevožena razdalja do postanka: ■ Gibanje točke, vržene na kota proti obzorju v enotnem gravitacijskem polju brez upoštevanja zračnega upora. Če izločimo čas iz enačb gibanja, dobimo enačbo trajektorije: Čas letenja se določi tako, da se koordinata y enači z ničlo: Domet leta se določi z zamenjavo čas letenja:

11 diapozitiv
Predavanje 3 Premočrtno nihanje materialne točke - Nihanje materialne točke se pojavi pod pogojem, da obstaja obnovitvena sila, ki teži k vrnitvi točke v ravnotežni položaj za kakršno koli odstopanje od tega položaja. 9 Obstaja obnovitvena sila, ravnotežni položaj je stabilen Ni obnovitvene sile, ravnotežni položaj je nestabilen Ni obnovitvene sile, ravnotežni položaj je indiferenten Vedno je usmerjena proti ravnotežnemu položaju, vrednost je premosorazmerna z linearnim raztezkom (skrajšanjem) vzmeti, ki je enaka odstopanju telesa od ravnotežnega položaja: c je koeficient togosti vzmeti, številčno enak sila, pod katero vzmet spremeni svojo dolžino za eno, merjeno v N / m v sistemu SI. x y O Vrste tresljajev materialne točke: 1. Proste vibracije (brez upoštevanja upora medija). 2. Prosta nihanja ob upoštevanju upora medija (dušena nihanja). 3. Prisilne vibracije. 4. Prisilna nihanja ob upoštevanju upora medija. ■ Prosta nihanja - nastanejo pod delovanjem le obnovitvene sile. Zapišimo osnovni zakon dinamike: Izberimo koordinatni sistem s središčem na ravnotežnem položaju (točka O) in projiciramo enačbo na os x: Dobljeno enačbo privedemo v standardno (kanonično) obliko: Ta enačba je homogena linearna diferencialna enačba drugega reda, katere obliko rešitve določajo korenine značilnosti enačbe, pridobljene z univerzalno substitucijo: Korenine karakteristične enačbe so imaginarne in enake: Splošna rešitev diferencialne enačbe ima obliko: Hitrost točke: Začetni pogoji: Določite konstante: Torej ima enačba prostih nihanj obliko: Enačbo lahko predstavimo z izrazom z enim členom: kjer je a amplituda, - začetna faza. Novi konstanti a in - sta povezani s konstantama C1 in C2 z relacijama: Definirajmo a in: Razlog za nastanek prostih nihanj je začetni premik x0 in/ali začetna hitrost v0.

12 diapozitiv
10 Predavanje 3 (nadaljevanje 3.2) Dušeno nihanje materialne točke - Nihanje materialne točke se pojavi ob prisotnosti obnovitvene sile in sile upora proti gibanju. Odvisnost sile upora proti gibanju od premika ali hitrosti je določena s fizično naravo medija ali povezave, ki ovira gibanje. Najenostavnejša odvisnost je linearna odvisnost od hitrosti (viskozni upor): - koeficient viskoznosti xy O Osnovna enačba dinamike: Projekcija enačbe dinamike na os: Enačbo privedemo v standardno obliko: kjer ima karakteristična enačba korenine: Splošna rešitev te diferencialne enačbe ima drugačno obliko, odvisno od vrednosti korenov: 1. n< k – случай малого вязкого сопротивления: - корни комплексные, различные. или x = ae-nt x = -ae-nt Частота затухающих колебаний: Период: T* Декремент колебаний: ai ai+1 Логарифмический декремент колебаний: Затухание колебаний происходит очень быстро. Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени. 2. n >k - primer visoke viskozne odpornosti: - prave korenine, razl. ali - te funkcije so aperiodične: 3. n = k: - koreni so realni, večkratni. te funkcije so tudi aperiodične:

13 diapozitiv
Predavanje 3 (nadaljevanje 3.3) Klasifikacija rešitev prostih nihanj. Vzmetne povezave. enakovredno trdoto. y y 11 Dif. Znak enačbe. Enačba Roots char. enačba Reševanje diferencialne enačbe Graf nk n=k

14 diapozitiv
Predavanje 4 Prisilne vibracije materialne točke - Skupaj z obnovitveno silo deluje periodično spreminjajoča se sila, ki se imenuje moteča sila. Motilna sila ima lahko drugačno naravo. Na primer, v določenem primeru inercialni učinek neuravnotežene mase m1 vrtečega se rotorja povzroči harmonično spreminjajoče se projekcije sile: Glavna enačba dinamike: Projekcija enačbe dinamike na os: Enačbo približamo standardu oblika: 12 Rešitev te nehomogene diferencialne enačbe je sestavljena iz dveh delov x = x1 + x2: x1 je splošna rešitev ustrezne homogene enačbe in x2 je posebna rešitev nehomogene enačbe: Izberemo določeno rešitev v obliki desna stran: Dobljena enakost mora biti izpolnjena za kateri koli t . Potem: ali Tako, s istočasno delovanje obnavljajoče in moteče sile, materialna točka izvaja kompleksno nihajno gibanje, ki je posledica seštevanja (superpozicije) prostih (x1) in prisilnih (x2) vibracij. Če je p< k (вынужденные колебания малой частоты), то фаза колебаний совпадает с фазой возмущающей силы: В итоге полное решение: или Общее решение: Постоянные С1 и С2, или a и определяются из начальных условий с использованием полного решения (!): Таким образом, частное решение: Если p >k (prisilna nihanja visoke frekvence), potem je faza nihanja nasprotna fazi moteče sile:

15 diapozitiv
Predavanje 4 (nadaljevanje 4.2) 13 Dinamični koeficient - razmerje med amplitudo prisilnih nihanj in statičnim odklonom točke pod delovanjem konstantne sile H = const: Amplituda prisilnih nihanj: Statični odklon je mogoče najti iz ravnotežna enačba: Tukaj: Zato: Tako na str< k (малая частота вынужденных колебаний) коэффициент динамичности: При p >k (visoka frekvenca prisilnih nihanj) dinamični koeficient: Resonanca - nastane, ko frekvenca prisilnih nihanj sovpada s frekvenco lastnih nihanj (p = k). Najpogosteje se to zgodi pri zagonu in ustavitvi vrtenja slabo uravnoteženih rotorjev, nameščenih na elastičnih vzmetenjih. Diferencialna enačba nihanja z enakimi frekvencami: določene rešitve v obliki desne strani ni mogoče vzeti, ker dobimo linearno odvisno rešitev (glej splošno rešitev). Splošna rešitev: Nadomestek v diferencialni enačbi: Vzemimo določeno rešitev v obliki in izračunajmo izpeljanke: Tako dobimo rešitev: ali Prisilna nihanja pri resonanci imajo amplitudo, ki se neomejeno povečuje sorazmerno s časom. Vpliv upora proti gibanju pri prisilnih vibracijah. Diferencialna enačba ob prisotnosti viskoznega upora ima obliko: Splošna rešitev je izbrana iz tabele (predavanje 3, str. 11) glede na razmerje n in k (glej). Vzamemo določeno rešitev v obliki in izračunamo odvodke: Nadomestimo v diferencialno enačbo: Ko izenačimo koeficiente za identične trigonometrične funkcije, dobimo sistem enačb: Dvignemo obe enačbi na potenco in ju seštejemo, dobimo amplitudo prisilna nihanja: Če drugo enačbo delimo s prvo, dobimo fazni premik prisilnih nihanj: Tako je enačba gibanja za prisilna nihanja ob upoštevanju upora proti gibanju na primer za n< k (малое сопротивление): Вынужденные колебания при сопротивлении движению не затухают. Частота и период вынужденных колебаний равны частоте и периоду изменения возмущающей силы. Коэффициент динамичности при резонансе имеет конечную величину и зависит от соотношения n и к.

16 diapozitiv
Predavanje 5 Relativno gibanje materialne točke - Predpostavimo, da se gibljivi (neinercialni) koordinatni sistem Oxyz giblje po nekem zakonu glede na fiksni (inercialni) koordinatni sistem O1x1y1z1. Gibanje materialne točke M (x, y, z) glede na mobilni sistem Oxyz je relativno, glede na nepremični sistem O1x1y1z1 je absolutno. Gibanje mobilnega sistema Oxyz glede na fiksni sistem O1x1y1z1 je prenosno gibanje. 14 z x1 y1 z1 O1 xy M xyz O Osnovna enačba dinamike: Absolutni pospešek točke: Absolutni pospešek točke nadomestimo v glavno enačbo dinamike: Prenesimo člene s translacijskim in Coriolisovim pospeškom na desno stran: preneseni izrazi imajo dimenzijo sil in se štejejo za ustrezne vztrajnostne sile, enake: Potem lahko relativno gibanje točke štejemo za absolutno, če delujočim silam dodamo translacijsko in Coriolisovo vztrajnostno silo: V projekcijah na osi gibljivega koordinatnega sistema imamo: vrtenje je enakomerno, potem je εe = 0: 2. Translacijsko krivolinijsko gibanje: Če je gibanje premočrtno, potem = : Če je gibanje premočrtno in enakomerno, potem je gibljivi sistem inercialen in relativno gibanje lahko štejemo za absolutno: noben mehanski pojav ne more zaznati pravolinijske uniforme gibanje (načelo relativnosti klasične mehanike). Vpliv vrtenja Zemlje na ravnotežje teles - Predpostavimo, da je telo v ravnotežju na Zemljinem površju na poljubni širini φ (vzporednice). Zemlja se vrti okoli svoje osi od zahoda proti vzhodu s kotno hitrostjo: polmer Zemlje je približno 6370 km. S R je skupna reakcija negladke površine. G - sila privlačnosti Zemlje v središče. Ф - vztrajnostna centrifugalna sila. Pogoj relativnega ravnotežja: Rezultanta sil privlačnosti in vztrajnosti je sila gravitacije (teža): Velikost sile teže (teže) na površini Zemlje je P = mg. Centrifugalna vztrajnostna sila je majhen del sile gravitacije: Majhen je tudi odklon sile teže od smeri privlačne sile: Tako je vpliv vrtenja Zemlje na ravnovesje teles izjemno majhen. in se pri praktičnih izračunih ne upošteva. Največja vrednost inercialne sile (pri φ = 0 - na ekvatorju) je le 0,00343 vrednosti gravitacije

17 diapozitiv
Predavanje 5 (nadaljevanje 5.2) 15 Vpliv vrtenja Zemlje na gibanje teles v Zemljinem gravitacijskem polju - Recimo, da telo pade na Zemljo z določene višine H nad zemeljskim površjem na zemljepisni širini φ . Izberimo gibljiv referenčni okvir, togo povezan z Zemljo, ki usmerja osi x, y tangencialno na vzporednico in na poldnevnik: Relativna enačba gibanja: Tukaj je majhnost centrifugalne sile vztrajnosti v primerjavi s silo gravitacije upoštevati. Tako je sila teže poistovetena s silo gravitacije. Poleg tega domnevamo, da je gravitacija usmerjena pravokotno na zemeljsko površino zaradi majhnosti njenega upogiba, kot je opisano zgoraj. Coriolisov pospešek je enak in usmerjen vzporedno z osjo y proti zahodu. Coriolisova vztrajnostna sila je usmerjena v nasprotno smer. Enačbo relativnega gibanja projiciramo na os: Rešitev prve enačbe daje: Začetne pogoje: Rešitev tretje enačbe daje: Začetne pogoje: Tretja enačba ima obliko: Začetni pogoji: Njena rešitev daje: Dobljeno rešitev kaže, da se telo ob padcu odmakne proti vzhodu. Izračunajmo vrednost tega odstopanja, na primer pri padcu z višine 100 m. Čas padca najdemo iz rešitve druge enačbe: Tako je vpliv Zemljine rotacije na gibanje teles izjemno majhen. za praktične višine in hitrosti in se pri tehničnih izračunih ne upošteva. Rešitev druge enačbe pomeni tudi obstoj hitrosti vzdolž osi y, ki bi prav tako morala povzročiti in povzročiti ustrezen pospešek in Coriolisovo vztrajnostno silo. Vpliv te hitrosti in z njo povezane vztrajnostne sile na spremembo gibanja bo celo manjši od obravnavane Coriolisove vztrajnostne sile, povezane z navpično hitrostjo.

18 diapozitiv
Predavanje 6 Dinamika mehanskega sistema. Sistem materialnih točk ali mehanski sistem - Nabor materialnih točk ali tistih materialnih točk, ki jih združujejo splošni zakoni interakcije (položaj ali gibanje vsake od točk ali telesa je odvisno od položaja in gibanja vseh drugih). sistem prostih točk - katerega gibanje ni omejeno z nobenimi povezavami (na primer planetarni sistem, v katerem se planeti obravnavajo kot materialne točke). Sistem neprostih točk ali neprosti mehanski sistem - gibanje materialnih točk ali teles je omejeno z omejitvami, ki so naložene sistemu (na primer mehanizem, stroj itd.). 16 Sile, ki delujejo na sistem. Poleg predhodno obstoječe klasifikacije sil (aktivne in reaktivne sile) se uvaja nova klasifikacija sil: 1. Zunanje sile (e) - delujejo na točke in telesa sistema iz točk ali teles, ki niso del tega sistem. 2. Notranje sile (i) - sile interakcije med materialnimi točkami ali telesi, vključenimi v dani sistem. Ista sila je lahko tako zunanja kot notranja sila. Vse je odvisno od tega, kateri mehanski sistem se upošteva. Na primer: V sistemu Sonca, Zemlje in Lune so vse gravitacijske sile med njimi notranje. Če upoštevamo sistem Zemlje in Lune, so gravitacijske sile, ki delujejo s strani Sonca, zunanje: CZL Na podlagi zakona delovanja in reakcije vsaka notranja sila Fk ustreza drugi notranji sili Fk', enaki po absolutni vrednosti in nasprotni po smer. Iz tega sledita dve izjemni lastnosti notranjih sil: Glavni vektor vseh notranjih sil sistema je enak nič: Glavni moment vseh notranjih sil sistema glede na katero koli središče je enak nič: Ali v projekcijah na koordinato osi: Opomba. Čeprav so te enačbe podobne ravnotežnim enačbam, niso, saj notranje sile delujejo na različne točke ali telesa sistema in lahko povzročijo, da se te točke (telesa) premikajo ena glede na drugo. Iz teh enačb izhaja, da notranje sile ne vplivajo na gibanje sistema, ki ga obravnavamo kot celoto. Masno središče sistema materialnih točk. Za opis gibanja sistema kot celote je uvedena geometrijska točka, imenovana središče mase, katere polmer je določen z izrazom, kjer je M masa celotnega sistema: ali v projekcijah na koordinato osi: Formule za težišče so podobne tistim za težišče. Vendar je pojem središča mase bolj splošen, saj ni povezan z gravitacijskimi silami ali silami gravitacije.

19 diapozitiv
6. predavanje (nadaljevanje 6.2) 17 Izrek o gibanju masnega središča sistema - Razmislimo o sistemu n materialnih točk. Sile, ki delujejo na vsako točko, razdelimo na zunanje in notranje ter jih nadomestimo z ustreznima rezultantama Fke in Fki. Za vsako točko zapišimo osnovno enačbo dinamike: ali Te enačbe seštejmo po vseh točkah: Na levi strani enačbe bomo uvedli mase pod predznakom odvoda in vsoto odvodov zamenjali z izpeljanko. od vsote: Iz definicije središča mase: Nadomestimo v dobljeno enačbo: dobimo ali: Zmnožek mase sistema in pospeška njegove mase središča je enak glavnemu vektorju zunanjih sil. V projekcijah na koordinatne osi: Masno središče sistema se premika kot materialna točka z maso, enaka masi celoten sistem, na katerega delujejo vse zunanje sile, ki delujejo na sistem. Posledice iz izreka o gibanju masnega središča sistema (zakoni ohranjanja): 1. Če je v časovnem intervalu glavni vektor zunanjih sil sistema nič, Re = 0, potem je hitrost središča mase je konstantna, vC = const (središče mase se giblje enakomerno pravokotno - zakon ohranjanja gibanja središča mase). 2. Če je v časovnem intervalu projekcija glavnega vektorja zunanjih sil sistema na os x enaka nič, Rxe = 0, potem je hitrost središča mase vzdolž osi x konstantna, vCx = const (središče mase se premika enakomerno vzdolž osi). Podobne trditve veljajo za osi y in z. Primer: Dve osebi z maso m1 in m2 sta v čolnu mase m3. V začetnem trenutku je čoln z ljudmi miroval. Določite premik čolna, če se je oseba z maso m2 premaknila do premca čolna na razdalji a. 3. Če je v časovnem intervalu glavni vektor zunanjih sil sistema enak nič, Re = 0 in je v začetnem trenutku hitrost središča mase nič, vC = 0, potem je vektor polmera središče mase ostane konstantno, rC = const (središče mase miruje je zakon o ohranitvi položaja središča mase). 4. Če je v časovnem intervalu projekcija glavnega vektorja zunanjih sil sistema na os x enaka nič, je Rxe = 0 in je v začetnem trenutku hitrost središča mase vzdolž te osi enaka nič , vCx = 0, potem ostane koordinata središča mase vzdolž osi x konstantna, xC = const (središče mase se ne premika vzdolž te osi). Podobne trditve veljajo za osi y in z. 1. Predmet gibanja (čoln z ljudmi): 2. Odvržemo povezave (voda): 3. Povezavo zamenjamo z reakcijo: 4. Seštejemo aktivne sile: 5. Zapiši izrek o masnem središču: Projektirajte na os x: O Ugotovite, kako daleč morate prenesti do osebe z maso m1, da bo čoln ostal na mestu: Čoln se bo premaknil za razdaljo l v nasprotni smeri.

20 diapozitiv
Predavanje 7 Impulz sile je mera mehanske interakcije, ki označuje prenos mehanskega gibanja od sil, ki delujejo na točko za določeno časovno obdobje: 18 Pri projekcijah na koordinatne osi: V primeru konstantne sile: V projekcijah na koordinatne osi: na točko sile v istem časovnem intervalu: Pomnožimo z dt: Integriraj v danem časovnem intervalu: Zagon točke je mera mehanskega gibanja, določena z vektorjem, enakim zmnožku mase točka in njen vektor hitrosti: Izrek o spremembi gibalne količine sistema - Razmislite o sistemu n materialnih točk. Sile, ki delujejo na vsako točko, razdelimo na zunanje in notranje ter jih nadomestimo z ustreznima rezultantama Fke in Fki. Za vsako točko zapišemo osnovno enačbo dinamike: ali Količina gibanja sistema materialnih točk - geometrijska vsota količin gibanja materialnih točk: Po definiciji težišča mase: Vektor gibalne količine sistema je enak zmnožku mase celotnega sistema in vektorja hitrosti središča mase sistema. Nato: V projekcijah na koordinatne osi: Časovni izvod vektorja gibalne obremenitve sistema je enak glavnemu vektorju zunanjih sil sistema. Seštejmo te enačbe po vseh točkah: Na levi strani enačbe uvedemo mase pod predznakom odvoda in nadomestimo vsoto odvodov z izpeljanko vsote: Iz definicije gibalne količine sistema: V projekcijah na koordinatne osi:

21 diapozitiv
Eulerjev izrek - Uporaba izreka o spremembi gibalne količine sistema na gibanje neprekinjenega medija (vode). 1. Za predmet gibanja izberemo prostornino vode, ki se nahaja v krivolinijskem kanalu turbine: 2. Priključke zavržemo in njihovo delovanje nadomestimo z reakcijami (Rpov - rezultanta površinskih sil) 3. Dodajte aktivne sile (Rb - rezultanta telesnih sil): 4. Zapiši izrek o spremembi gibalne količine sistema: Količina gibanja vode v časih t0 in t1 bo predstavljena kot vsote: Sprememba količine gibalne količine vode v časovnem intervalu : Sprememba gibalne količine vode v neskončno majhnem časovnem intervalu dt: , kjer F1 F2 Če vzamemo zmnožek gostote, površine preseka in hitrosti na sekundno maso, dobimo: Nadomestimo diferencial gibalne količine sistema v izrek o spremembi , dobimo: Posledice iz izreka o spremembi gibalne količine sistema (zakoni ohranjanja): 1. Če je v časovnem intervalu glavni vektor zunanjih sil sistema enak nič, Re = 0, potem je v časovnem intervalu glavni vektor zunanjih sil sistema enak nič. kvantitetno vektorsko gibanje je konstantno, Q = const je zakon o ohranitvi gibalne količine sistema). 2. Če je v časovnem intervalu projekcija glavnega vektorja zunanjih sil sistema na os x enaka nič, Rxe = 0, potem je projekcija gibalne količine sistema na os x konstantna, Qx = konst. Podobne trditve veljajo za osi y in z. 7. predavanje (nadaljevanje 7.2) Primer: Granata mase M, ki je letela s hitrostjo v, je eksplodirala na dva dela. Hitrost enega od drobcev mase m1 se je v smeri gibanja povečala na vrednost v1. Določite hitrost drugega fragmenta. 1. Predmet gibanja (granata): 2. Objekt je prosti sistem, ni povezav in njihovih reakcij. 3. Dodajte aktivne sile: 4. Zapišite izrek o spremembi zagona: Projektirajte na os: β Razdelite spremenljivke in integrirajte: Desni integral je skoraj nič, ker čas eksplozije t

22 diapozitiv
Predavanje 7 (nadaljevanje 7.3) 20 Kotni moment točke ali kinetični moment gibanja glede na določeno središče je mera mehanskega gibanja, določena z vektorjem, ki je enak vektorskemu produktu vektorja polmera materialne točke in vektor njegove gibalne količine: kinetični moment sistema materialnih točk glede na določeno središče je geometrijski vsota momentov števila gibov vseh materialnih točk glede na isto središče: v projekcijah na os: v projekcijah na os: Izrek o spremembi momenta gibalne količine sistema - Razmislite o sistemu n materialnih točk. Sile, ki delujejo na vsako točko, razdelimo na zunanje in notranje ter jih nadomestimo z ustreznima rezultantama Fke in Fki. Za vsako točko zapišimo osnovno enačbo dinamike: ali Seštejmo te enačbe za vse točke: Vsoto odvodov zamenjamo z izpeljanko vsote: Izraz v oklepaju je moment gibanja sistema. Od tukaj: Vsako od enakosti vektorsko pomnožimo s polmerom-vektorjem na levi: Poglejmo, ali je mogoče predznak odvoda vzeti izven vektorskega produkta: Tako smo dobili: center. V projekcijah na koordinatne osi: Odvod momenta gibanja sistema glede na neko os v času je enak glavnemu momentu zunanjih sil sistema glede na isto os.

23 diapozitiv
Predavanje 8 21 ■ Posledice iz izreka o spremembi gibalne količine sistema (ohranjevalni zakoni): 1. Če je v časovnem intervalu vektor glavnega momenta zunanjih sil sistema glede na določeno središče enak. na nič, MOe = 0, potem je vektor kotne količine sistema glede na isto središče konstanten, KO = const je zakon o ohranitvi gibalne količine sistema). 2. Če v časovnem intervalu Glavna točka zunanje sile sistema glede na os x enake nič, Mxe = 0, potem je kotni moment sistema glede na os x konstanten, Kx = const. Podobne trditve veljajo za osi y in z. 2. Vztrajnostni moment togega telesa okoli osi: Vztrajnostni moment materialne točke okoli osi je enak zmnožku mase točke in kvadrata razdalje točke do osi. Vztrajnostni moment togega telesa okoli osi je enak vsoti produktov mase vsake točke in kvadrata oddaljenosti te točke od osi. ■ Elementi teorije vztrajnostnih momentov - Pri rotacijskem gibanju togega telesa je mera vztrajnosti (upora proti spremembi gibanja) vztrajnostni moment okoli osi vrtenja. Razmislite o osnovnih konceptih definicije in metodah za izračun vztrajnostnih momentov. 1. Vztrajnostni moment materialne točke okoli osi: Pri prehodu iz diskretne majhne mase v neskončno majhno maso točke je meja takšne vsote določena z integralom: aksialni vztrajnostni moment togega telesa. . Poleg aksialnega vztrajnostnega momenta togega telesa obstajajo še druge vrste vztrajnostnih momentov: centrifugalni vztrajnostni moment togega telesa. polarni vztrajnostni moment togega telesa. 3. Izrek o vztrajnostnih momentih togega telesa glede vzporednih osi - formula za prehod na vzporedne osi: Vztrajnostni moment okoli referenčne osi Statični vztrajnostni momenti glede referenčnih osi Telesna masa Razdalja med osi z1 in z2 Tako : trenutki so nič:

24 diapozitiv
Predavanje 8 (nadaljevanje 8.2) 22 Vztrajnostni moment enotne palice konstantnega prereza okoli osi: xz L Izberite elementarni volumen dV = Adx na razdalji x: x dx Osnovna masa: Izračunajte vztrajnostni moment okoli osrednje osi (prehaja skozi težišče), je dovolj, da spremenite lokacijo osi in nastavite meje integracije (-L/2, L/2). Tukaj prikazujemo formulo za prehod na vzporedne osi: zС 5. Vztrajnostni moment homogenega trdnega valja okoli osi simetrije: H dr r Izpostavimo elementarni volumen dV = 2πrdrH (tanek valj polmera r) : Osnovna masa: Tukaj uporabljamo formulo volumna valja V=πR2H. Za izračun vztrajnostnega momenta votlega (debelega) valja je dovolj, da nastavite integracijske meje od R1 do R2 (R2> R1): 6. Vztrajnostni moment tankega valja okoli osi simetrije (t

25 diapozitiv
Predavanje 8 (nadaljevanje 8.3) 23 ■ Diferencialna enačba vrtenja togega telesa okoli osi: Napišimo izrek o spreminjanju kotne količine togega telesa, ki se vrti okoli nepremične osi: Moč vrtenja togega telesa je: Moment zunanjih sil okoli osi vrtenja je enak navoru (reakcije in sila ne ustvarjajo gravitacijskih momentov): V izrek nadomestimo kinetični moment in navor Primer: Dve osebi enake teže G1 = G2 visita na vrženi vrvi nad trdnim blokom z utežjo G3 = G1/4. V nekem trenutku je eden od njiju začel plezati po vrvi z relativno hitrostjo u. Določite hitrost dviga vsake osebe. 1. Izberite predmet gibanja (blok z ljudmi): 2. Zavrzite povezave (podporna naprava bloka): 3. Zamenjajte povezavo z reakcijami (ležaj): 4. Dodajte aktivne sile (teža): 5. Zapišite izrek o spreminjanju kinetičnega momenta sistema glede na os vrtenja bloka: R Ker je moment zunanjih sil enak nič, mora kinetični moment ostati konstanten: V začetnem trenutku časa t = 0 je je bila ravnotežna in Kz0 = 0. Po začetku gibanja ene osebe glede na vrv se je celoten sistem začel premikati, vendar mora kinetični moment sistema ostati enak nič: Kz = 0. Kotni moment sistem je vsota kotnih momentov obeh ljudi in bloka: Tukaj je v2 hitrost druge osebe, enaka hitrosti kabla, Primer: Določite obdobje majhnih prostih nihanj homogene palice mase M in dolžine l, obešena z enim koncem na fiksno vrtilno os. Ali: v primeru majhnih nihanj sinφ φ: obdobje nihanja: vztrajnostni moment droga:

26 diapozitiv
Predavanje 8 (nadaljevanje 8.4 - dodatno gradivo) 24 ■ Osnovna teorija žiroskopa: Žiroskop je togo telo, ki se vrti okoli osi simetrije materiala, katerega ena od točk je fiksna. Prosti žiroskop je pritrjen tako, da njegovo središče mase ostane nepremično, os vrtenja pa poteka skozi središče mase in lahko zavzame poljuben položaj v prostoru, t.j. os vrtenja spreminja svoj položaj kot os lastne rotacije telesa med sferičnim gibanjem. Glavna predpostavka približne (elementarne) teorije žiroskopa je, da velja, da je vektor zagona (kinetični moment) rotorja usmerjen vzdolž lastne osi vrtenja. Tako se kljub dejstvu, da v splošnem primeru rotor sodeluje v treh vrtenjih, upošteva le kotno hitrost lastnega vrtenja ω = dφ/dt. Razlog za to je, da se v sodobni tehnologiji rotor žiroskopa vrti s kotno hitrostjo reda 5000-8000 rad/s (približno 50000-80000 vrt/min), medtem ko sta drugi dve kotni hitrosti povezani s precesijo in nutacijo lastne osi. vrtenja deset tisočkrat manjša od te hitrosti. Glavna lastnost prostega žiroskopa je, da os rotorja ohranja isto smer v prostoru glede na inercialni (zvezdni) referenčni sistem (dokazuje Foucaultovo nihalo, ki ohranja ravnino nihanja nespremenjeno glede na zvezde, 1852). To izhaja iz zakona o ohranjanju kinetičnega momenta glede na središče mase rotorja, pod pogojem, da se zanemari trenje v ležajih osi vzmetenja rotorja, zunanjega in notranjega okvirja: Delovanje sile na os prostega žiroskop. V primeru sile, ki deluje na os rotorja, moment zunanjih sil glede na središče mase ni enak nič: sila ω ω С in proti vektorju momenta te sile, t.j. se ne vrti okoli osi x (notranje vzmetenje), ampak okoli y-osi (zunanje vzmetenje). Po prenehanju sile bo os rotorja ostala v enakem položaju, ki ustreza zadnjemu času sile, ker od tega trenutka postane trenutek zunanjih sil spet enak nič. V primeru kratkotrajnega delovanja sile (udarca) os žiroskopa praktično ne spremeni svojega položaja. Tako hitro vrtenje rotorja daje žiroskopu možnost, da se zoperstavi naključnim vplivom, ki želijo spremeniti položaj osi vrtenja rotorja, in s stalnim delovanjem sile ohranja položaj ravnine, pravokotne na delovna sila, v kateri leži os rotorja. Te lastnosti se uporabljajo pri delovanju inercialnih navigacijskih sistemov.
Kot del vsakega učnega načrta se študij fizike začne z mehaniko. Ne iz teoretične, ne iz uporabne in ne računske, ampak iz dobre stare klasične mehanike. Ta mehanika se imenuje tudi Newtonova mehanika. Po legendi se je znanstvenik sprehajal po vrtu, videl padec jabolka in prav ta pojav ga je spodbudil, da je odkril zakon univerzalne gravitacije. Seveda je zakon vedno obstajal in Newton mu je dal le obliko, razumljivo ljudem, vendar je njegova zasluga neprecenljiva. V tem članku ne bomo čim bolj podrobno opisovali zakonov Newtonove mehanike, ampak bomo orisali osnove, osnovna znanja, definicije in formule, ki vam lahko vedno igrajo na roko.
Mehanika je veja fizike, veda, ki preučuje gibanje materialnih teles in interakcije med njimi.
Sama beseda je grškega izvora in se prevaja kot "umetnost gradnje strojev". Toda pred gradnjo strojev nas čaka še dolga pot, zato pojdimo po stopinjah naših prednikov in preučevali bomo gibanje kamnov, vrženih pod kotom proti obzorju, in jabolk, ki padajo na glave z višine h.

Zakaj se študij fizike začne z mehaniko? Ker je povsem naravno, ne da bi ga začeli iz termodinamičnega ravnovesja?!
Mehanika je ena najstarejših ved, zgodovinsko pa se je študij fizike začel prav pri temeljih mehanike. Postavljeni v okvir časa in prostora, ljudje pravzaprav ne bi mogli začeti iz nečesa drugega, ne glede na to, kako so si želeli. Gibajoča se telesa so prva stvar, na katero smo pozorni.
Kaj je gibanje?
Mehansko gibanje je sprememba položaja teles v prostoru drug glede na drugega skozi čas.
Po tej definiciji povsem naravno pridemo do koncepta referenčnega okvira. Spreminjanje položaja teles v prostoru glede na drugo. Ključne besede tukaj: drug glede na drugega . Konec koncev se potnik v avtomobilu giblje glede na osebo, ki stoji ob cesti, z določeno hitrostjo in počiva glede na soseda na bližnjem sedežu in se premika z neko drugo hitrostjo glede na potnika v avtomobilu, ki jih prehiteva.

Zato potrebujemo, da bi normalno izmerili parametre premikajočih se predmetov in se ne zmedli referenčni sistem - togo medsebojno povezano referenčno telo, koordinatni sistem in ura. Zemlja se na primer giblje okoli sonca v heliocentričnem referenčnem okviru. V vsakdanjem življenju skoraj vse meritve izvajamo v geocentričnem referenčnem sistemu, ki je povezan z Zemljo. Zemlja je referenčno telo, glede na katerega se premikajo avtomobili, letala, ljudje, živali.

Mehanika ima kot znanost svojo nalogo. Naloga mehanike je, da v vsakem trenutku pozna položaj telesa v prostoru. Z drugimi besedami, mehanika konstruira matematični opis gibanja in najde povezave med fizikalnimi količinami, ki ga označujejo.
Za napredek potrebujemo pojem » materialna točka ". Pravijo, da je fizika eksaktna znanost, a fiziki vedo, koliko približkov in predpostavk je treba narediti, da bi se strinjali prav o tej natančnosti. Nihče še ni videl materialne točke ali vohal idealnega plina, vendar obstajajo! Le z njimi je veliko lažje živeti.
Materialna točka je telo, katerega velikost in obliko lahko v kontekstu tega problema zanemarimo.
Odseki klasične mehanike
Mehanika je sestavljena iz več delov
- Kinematika
- Dinamika
- Statika
Kinematika od fizična točka vid preučuje, kako se telo premika. Z drugimi besedami, ta razdelek obravnava kvantitativne značilnosti gibanja. Najdi hitrost, pot - tipične naloge kinematike
Dinamika rešuje vprašanje, zakaj se premika tako, kot se. To pomeni, da upošteva sile, ki delujejo na telo.
Statika preučuje ravnotežje teles pod delovanjem sil, torej odgovarja na vprašanje: zakaj sploh ne pade?
Meje uporabnosti klasične mehanike
Klasična mehanika ne trdi več, da je znanost, ki razlaga vse (na začetku prejšnjega stoletja je bilo vse povsem drugače) in ima jasen obseg uporabnosti. Na splošno veljajo zakoni klasične mehanike za svet, ki ga poznamo po velikosti (makrosvet). Nehajo delovati v primeru sveta delcev, ko klasično mehaniko nadomesti kvantna mehanika. Tudi klasična mehanika ni uporabna za primere, ko se gibanje teles odvija s hitrostjo, ki je blizu svetlobni. V takih primerih postanejo izraziti relativistični učinki. Grobo rečeno, v okviru kvantne in relativistične mehanike - klasične mehanike, je to poseben primer, ko so dimenzije telesa velike, hitrost pa majhna.

Na splošno kvantni in relativistični učinki nikoli ne izginejo; potekajo tudi med običajnim gibanjem makroskopskih teles s hitrostjo, ki je veliko nižja od svetlobne. Druga stvar je, da je delovanje teh učinkov tako majhno, da ne presega najbolj natančnih meritev. Klasična mehanika tako nikoli ne bo izgubila svojega temeljnega pomena.
V prihodnjih člankih bomo nadaljevali s preučevanjem fizikalnih osnov mehanike. Za boljše razumevanje mehanike se lahko vedno obrnete na naših avtorjev, ki so posamezno osvetlili temno točko najtežje naloge.
Teoretična mehanika- To je veja mehanike, ki določa osnovne zakone mehanskega gibanja in mehanske interakcije materialnih teles.
Teoretična mehanika je veda, v kateri se proučujejo gibanja teles skozi čas (mehanska gibanja). Služi kot osnova za druge oddelke mehanike (teorija elastičnosti, odpornost materialov, teorija plastičnosti, teorija mehanizmov in strojev, hidroaerodinamika) in številne tehnične discipline.
mehansko gibanje- to je sčasoma sprememba relativnega položaja materialnih teles v prostoru.
Mehanska interakcija- to je takšna interakcija, zaradi katere se spremeni mehansko gibanje ali se spremeni relativni položaj delov telesa.
Statika togega telesa
Statika- To je veja teoretične mehanike, ki se ukvarja s problemi ravnotežja trdnih teles in pretvorbe enega sistema sil v drugega, njemu enakovrednega.
- Osnovni pojmi in zakoni statike
- Popolnoma togo telo(trdno telo, telo) je materialno telo, v katerem se razdalja med nobenimi točkami ne spreminja.
- Materialna točka je telo, katerega dimenzije glede na pogoje problema lahko zanemarimo.
- ohlapno telo je telo, katerega gibanje ni omejeno.
- Nesvobodno (vezano) telo je telo, katerega gibanje je omejeno.
- Povezave- to so telesa, ki preprečujejo gibanje obravnavanega predmeta (telo ali sistem teles).
- Komunikacijska reakcija je sila, ki označuje delovanje vezi na togo telo. Če silo, s katero togo telo deluje na vez, upoštevamo kot delovanje, potem je reakcija vezi protiukrep. V tem primeru se sila - delovanje nanaša na povezavo, reakcija povezave pa na trdno telo.
- mehanski sistem je skupek med seboj povezanih teles ali materialnih točk.
- Trdno lahko obravnavamo kot mehanski sistem, katerega položaji in razdalja med točkami se ne spreminjajo.
- Moč je vektorska količina, ki označuje mehansko delovanje enega materialnega telesa na drugega.
Za silo kot vektor je značilna točka uporabe, smer delovanja in absolutna vrednost. Merska enota za modul sile je Newton. - črta sile je ravna črta, vzdolž katere je usmerjen vektor sile.
- Koncentrirana moč je sila, ki deluje na eni točki.
- Porazdeljene sile (razporejena obremenitev)- to so sile, ki delujejo na vse točke volumna, površine ali dolžine telesa.
Porazdeljena obremenitev je podana s silo, ki deluje na enoto prostornine (površina, dolžina).
Dimenzija porazdeljene obremenitve je N / m 3 (N / m 2, N / m). - Zunanja sila je sila, ki deluje iz telesa, ki ne spada v obravnavani mehanski sistem.
- notranja moč je sila, ki deluje na materialno točko mehanskega sistema iz druge materialne točke, ki pripada obravnavanemu sistemu.
- Sistem sile je celota sil, ki delujejo na mehanski sistem.
- Ploščati sistem sil je sistem sil, katerih linije delovanja ležijo v isti ravnini.
- Prostorski sistem sil je sistem sil, katerih linije delovanja ne ležijo v isti ravnini.
- Sistem konvergentnih sil je sistem sil, katerih linije delovanja se sekajo v eni točki.
- Samovoljni sistem sil je sistem sil, katerih linije delovanja se v eni točki ne sekajo.
- Ekvivalentni sistemi sil- to so sistemi sil, katerih zamenjava enega za drugega ne spremeni mehanskega stanja telesa.
Sprejeta oznaka: . - Ravnotežje Stanje, v katerem telo miruje ali se enakomerno giblje v ravni črti pod delovanjem sil.
- Uravnotežen sistem sil- to je sistem sil, ki ob delovanju na prosto trdno telo ne spremeni svojega mehanskega stanja (ne uravnoteži ga).
 .
. - rezultantna sila je sila, katere delovanje na telo je enakovredno delovanju sistema sil.
 .
. - Trenutek moči je vrednost, ki označuje rotacijsko sposobnost sile.
- Močni par je sistem dveh vzporednih enakih po absolutni vrednosti nasprotno usmerjenih sil.
Sprejeta oznaka: .
Pod delovanjem nekaj sil bo telo izvedlo rotacijsko gibanje. - Projekcija sile na os- to je odsek, zaprt med pravokotnici, potegnjenimi od začetka in konca vektorja sile na to os.
Projekcija je pozitivna, če smer segmenta sovpada s pozitivno smerjo osi. - Projekcija sile na ravnino je vektor na ravnini, zaprti med navpičnicama, vlečenima od začetka in konca vektorja sile na to ravnino.
- Zakon 1 (zakon vztrajnosti). Izolirana materialna točka miruje ali se giblje enakomerno in pravolinijsko.
Enakomerno in pravocrtno gibanje materialne točke je gibanje po vztrajnosti. Stanje ravnotežja materialne točke in togega telesa se ne razume le kot stanje mirovanja, temveč tudi kot gibanje po vztrajnosti. Za togo telo obstajajo različne vrste vztrajnostnega gibanja, na primer enakomerno vrtenje togega telesa okoli fiksne osi. - zakon 2. Togo telo je v ravnotežju pod delovanjem dveh sil le, če sta ti sili enaki po velikosti in usmerjeni v nasprotni smeri vzdolž skupne črte delovanja.
Ti dve sili se imenujeta uravnoteženi.
Na splošno velja, da so sile uravnotežene, če togo telo, na katerega delujejo te sile, miruje. - Zakon 3. Ne da bi motili stanje (beseda "stanje" tukaj pomeni stanje gibanja ali mirovanja) togega telesa, lahko dodajamo in zavržemo uravnovešajoče sile.
Posledica. Brez motenj v stanju togega telesa se sila lahko prenese vzdolž njegove linije delovanja na katero koli točko telesa.
Dva sistema sil se imenujeta enakovredna, če je mogoče enega od njiju nadomestiti z drugim, ne da bi pri tem motili stanje togega telesa. - Zakon 4. Rezultanta dveh sil, ki delujeta na eni točki, deluje na isti točki, je po absolutni vrednosti enaka diagonali paralelograma, zgrajenega na teh silah, in je usmerjena vzdolž tega
diagonale.
Modul rezultanta je: - Zakon 5 (zakon enakosti delovanja in reakcije). Sili, s katerimi dve telesi delujeta drug na drugega, sta enaki po velikosti in usmerjeni v nasprotni smeri vzdolž ene premočrtne črte.
Upoštevati je treba, da dejanje- sila, ki deluje na telo B, In opozicija- sila, ki deluje na telo AMPAK, niso uravnoteženi, saj so pritrjeni na različna telesa. - Zakon 6 (zakon utrjevanja). Ravnotežje netrdnega telesa se ne poruši, ko se strdi.
Ne smemo pozabiti, da so ravnotežni pogoji, ki so nujni in zadostni za togo telo, nujni, vendar nezadostni za ustrezno netogo telo. - Zakon 7 (zakon o sprostitvi obveznic). Neprosto trdno snov se lahko šteje za prosto, če je duševno osvobojeno vezi, pri čemer delovanje vezi nadomesti z ustreznimi reakcijami vezi.
- Povezave in njihove reakcije
- Gladka površina omejuje gibanje vzdolž normale na podporno površino. Reakcija je usmerjena pravokotno na površino.
- Zgibna premična opora omejuje gibanje telesa vzdolž normale na referenčno ravnino. Reakcija je usmerjena vzdolž normale na podporno površino.
- Zgibna fiksna podpora preprečuje vsako gibanje v ravnini, pravokotni na os vrtenja.
- Zgibna breztežna palica preprečuje gibanje telesa vzdolž linije palice. Reakcija bo usmerjena vzdolž linije palice.
- Slepa prekinitev preprečuje kakršno koli gibanje in vrtenje v ravnini. Njegovo delovanje je mogoče nadomestiti s silo, predstavljeno v obliki dveh komponent in par sil z momentom.




Kinematika
Kinematika- del teoretične mehanike, ki obravnava splošne geometrijske lastnosti mehanskega gibanja kot procesa, ki se dogaja v prostoru in času. Premikajoči se predmeti obravnavajo kot geometrijske točke ali geometrijska telesa.
- Osnovni pojmi kinematike
- Zakon gibanja točke (telesa) je odvisnost položaja točke (telesa) v prostoru od časa.
- Točkovna pot je lokus položajev točke v prostoru med njenim gibanjem.
- Točkovna (telesna) hitrost- to je značilnost časovne spremembe položaja točke (telesa) v prostoru.
- Točkovni (telesni) pospešek- to je značilnost spremembe v času hitrosti točke (telesa).
- Določanje kinematičnih značilnosti točke
- Točkovna pot
V vektorskem referenčnem sistemu je trajektorija opisana z izrazom: .
V koordinatnem referenčnem sistemu je trajektorija določena po zakonu gibanja točke in je opisana z izrazi z = f(x,y) v vesolju, oz y = f(x)- v letalu.
V naravnem referenčnem sistemu je pot vnaprej določena. - Določanje hitrosti točke v vektorskem koordinatnem sistemu
Pri določanju premika točke v vektorskem koordinatnem sistemu se razmerje gibanja in časovnega intervala imenuje povprečna vrednost hitrosti v tem časovnem intervalu: .
Če vzamemo časovni interval kot neskončno majhno vrednost, dobimo vrednost hitrosti v danem času (trenutna vrednost hitrosti): .
.
Vektor povprečne hitrosti je usmerjen vzdolž vektorja v smeri gibanja točke, vektor trenutne hitrosti je usmerjen tangencialno na trajektorijo v smeri gibanja točke.
Izhod: hitrost točke je vektorska količina, ki je enaka izvodu zakona gibanja glede na čas.
Lastnost izpeljanega finančnega instrumenta: časovni izvod katere koli vrednosti določa hitrost spremembe te vrednosti. - Določanje hitrosti točke v koordinatnem referenčnem sistemu
Stopnja spremembe koordinat točke: .
.
Modul polne hitrosti točke s pravokotnim koordinatnim sistemom bo enak: .
.
Smer vektorja hitrosti je določena s kosinusi krmilnih kotov: ,
,
kjer so koti med vektorjem hitrosti in koordinatnimi osmi. - Določanje hitrosti točke v naravnem referenčnem sistemu
Hitrost točke v naravnem referenčnem sistemu je opredeljena kot izpeljanka zakona gibanja točke: .
Glede na prejšnje ugotovitve je vektor hitrosti usmerjen tangencialno na trajektorijo v smeri gibanja točke in je v osi določen z eno samo projekcijo.
- Kinematika trdega telesa
- V kinematiki togih teles sta rešena dva glavna problema:
1) naloga gibanja in določanje kinematičnih značilnosti telesa kot celote;
2) določitev kinematičnih značilnosti točk telesa. - Translacijsko gibanje togega telesa
Translacijsko gibanje je gibanje, pri katerem ravna črta, potegnjena skozi dve točki telesa, ostane vzporedna s svojim prvotnim položajem.
izrek: pri translacijskem gibanju se vse točke telesa gibljejo po enakih trajektorijah in imajo v vsakem trenutku enake hitrosti in pospeške po velikosti in smeri.
Izhod: translacijsko gibanje togega telesa je določeno z gibanjem katere koli njegove točke, zato je naloga in študija njegovega gibanja reducirana na kinematiko točke. - Rotacijsko gibanje togega telesa okoli fiksne osi
Rotacijsko gibanje togega telesa okoli fiksne osi je gibanje togega telesa, pri katerem dve točki, ki pripadata telesu, ostaneta ves čas gibanja negibni.
Položaj telesa je določen s kotom vrtenja. Merska enota za kot je radian. (Radian je osrednji kot kroga, katerega dolžina loka je enaka polmeru, polni kot kroga vsebuje 2π radian.)
Zakon rotacijskega gibanja telesa okoli fiksne osi.
Kotno hitrost in kotni pospešek telesa bomo določili z diferenciacijsko metodo:
— kotna hitrost, rad/s;
— kotni pospešek, rad/s².
Če telo prerežemo z ravnino, pravokotno na os, izberemo točko na osi vrtenja IZ in poljubna točka M, potem bistvo M bo opisal okoli točke IZ krog polmera R. Med dt obstaja elementarna rotacija skozi kot , medtem ko točka M se bo premikal vzdolž poti za določeno razdaljo .
.
Modul linearne hitrosti: .
.
točkovni pospešek M z znano potjo določajo njegove komponente: ,
,
kje .
.
Kot rezultat dobimo formule
tangencialni pospešek: ;
;
normalen pospešek: .
.

Dinamika
Dinamika- To je veja teoretične mehanike, ki preučuje mehanska gibanja materialnih teles, odvisno od vzrokov, ki jih povzročajo.
- Osnovni pojmi dinamike
- vztrajnost- to je lastnost materialnih teles, da vzdržujejo stanje mirovanja ali enakomernega pravokotnega gibanja, dokler zunanje sile ne spremenijo tega stanja.
- Utež je kvantitativno merilo vztrajnosti telesa. Enota za maso je kilogram (kg).
- Materialna točka je telo z maso, katere dimenzije so pri reševanju tega problema zanemarjene.
- Masno središče mehanskega sistema je geometrijska točka, katere koordinate so določene s formulami:
kje m k , x k , y k , z k- masa in koordinate k- ta točka mehanskega sistema, m je masa sistema.
V enotnem gravitacijskem polju položaj težišča sovpada s položajem težišča. - Vztrajnostni moment materialnega telesa okoli osi je kvantitativna mera vztrajnosti med rotacijskim gibanjem.
Vztrajnostni moment materialne točke okoli osi je enak zmnožku mase točke in kvadrata oddaljenosti točke od osi: .
.
Vztrajnostni moment sistema (telesa) okoli osi je enak aritmetični vsoti vztrajnostnih momentov vseh točk:
- Sila vztrajnosti materialne točke je vektorska količina, ki je po absolutni vrednosti enaka zmnožku mase točke in modula pospeška in usmerjena nasprotno vektorju pospeška:
- Vztrajnostna sila materialnega telesa je vektorska količina, ki je po absolutni vrednosti enaka produktu telesne mase in modulu pospeška masnega središča telesa in usmerjena nasprotno vektorju pospeška središča mase: ,
kjer je pospešek težišča telesa. - Impulz elementarne sile je vektorska količina, enaka produktu vektorja sile z neskončno majhnim časovnim intervalom dt:
.
Skupni impulz sile za Δt je enak integralu osnovnih impulzov: .
. - Osnovno delo sile je skalar dA, enako skalarju
Ogled: ta članek je bil prebran 32852 krat
Pdf Izberite jezik... Ruski Ukrajinski Angleščina
Kratek pregled
Celotno gradivo je preneseno zgoraj, po izbiri jezika
- Statika
- Osnovni pojmi statike
- Vrste sile
- Aksiomi statike
- Povezave in njihove reakcije
- Sistem konvergentnih sil
- Metode za določanje rezultantnega sistema konvergentnih sil
- Ravnotežni pogoji za sistem konvergentnih sil
- Moment sile okoli središča kot vektor
- Algebraična vrednost momenta sile
- Lastnosti momenta sile okoli središča (točke)
- Teorija parov sil
- Seštevanje dveh vzporednih sil v isti smeri
- Seštevanje dveh vzporednih sil, usmerjenih v nasprotni smeri
- Pari moči
- Par izrekov o silah
- Pogoji za ravnotežje sistema parov sil
- Ročica vzvoda
- Samovoljni ravninski sistem sil
- Primeri zmanjševanja ravnega sistema sil na več navaden pogled
- Pogoji analiznega ravnotežja
- Center vzporednih sil. Težišče
- Center vzporednih sil
- Težišče togega telesa in njegove koordinate
- Težišče prostornine, ravnine in črte
- Metode za določanje položaja težišča
- Osnove Racsetov za moč
- Problemi in metode odpornosti materialov
- Razvrstitev obremenitve
- Razvrstitev konstrukcijskih elementov
- Deformacije palice
- Glavne hipoteze in načela
- Notranje sile. Metoda odseka
- Napetost
- Napetost in stiskanje
- Mehanske značilnosti materiala
- Dovoljene napetosti
- Trdota materiala
- Izrisi vzdolžnih sil in napetosti
- Shift
- Geometrijske značilnosti odsekov
- Torzija
- upogib
- Diferencialne odvisnosti pri upogibanju
- Upogibna trdnost
- normalni stresi. Izračun moči
- Strižne napetosti pri upogibanju
- Upogibna togost
- Elementi splošne teorije stresnega stanja
- Teorije moči
- Upogibanje z zasukom
- Kinematika
- Kinematika točke
- Točkovna pot
- Metode za določanje premikanja točke
- Točkovna hitrost
- točkovni pospešek
- Kinematika trdega telesa
- Translacijsko gibanje togega telesa
- Rotacijsko gibanje togega telesa
- Kinematika zobniških mehanizmov
- Ravnovzporedno gibanje togega telesa
- Kompleksno gibanje točk
- Kinematika točke
- Dinamika
- Osnovni zakoni dinamike
- Dinamika točke
- Diferencialne enačbe proste materialne točke
- Dva problema točkovne dinamike
- Dinamika togega telesa
- Klasifikacija sil, ki delujejo na mehanski sistem
- Diferencialne enačbe gibanja mehanskega sistema
- Splošni izreki dinamike
- Izrek o gibanju masnega središča mehanskega sistema
- Izrek o spremembi zagona
- Izrek o spremembi kotne količine
- Izrek o spremembi kinetične energije
- Sile, ki delujejo v strojih
- Sile pri vklopu čelnega zobnika
- Trenje v mehanizmih in strojih
- Drsno trenje
- kotalno trenje
- Učinkovitost
- Strojni deli
- Mehanski menjalniki
- Vrste mehanskih zobnikov
- Osnovni in izpeljani parametri mehanskih zobnikov
- prestave
- Zobniki s prilagodljivimi členi
- gredi
- Namen in razvrstitev
- Dizajnerski izračun
- Preverite izračun gredi
- Ležaji
- Drsni ležaji
- Kotalni ležaji
- Povezava delov stroja
- Vrste snemljivih in trajnih povezav
- Povezave s ključem
- Mehanski menjalniki
- Standardizacija norm, zamenljivost
- Tolerance in pristanki
- Enotni sistem toleranc in pristankov (ESDP)
- Odstopanje oblike in položaja
Format: pdf
Velikost: 4MB
ruski jezik
Primer izračuna čelnega zobnika
Primer izračuna čelnega zobnika. Izvedeni so bili izbor materiala, izračun dovoljenih napetosti, izračun kontaktne in upogibne trdnosti.
Primer reševanja problema upogibanja žarka
V primeru so narisani diagrami prečnih sil in upogibnih momentov, najde se nevaren odsek in izbran I-žarek. V problemu je bila analizirana konstrukcija diagramov z uporabo diferencialnih odvisnosti, izvedena je bila primerjalna analiza različnih prerezov žarkov.
Primer reševanja problema torzije gredi
Naloga je preizkusiti trdnost jeklene gredi za dani premer, material in dovoljene napetosti. Med reševanjem se gradijo diagrami navorov, strižnih napetosti in zavojnih kotov. Lastna teža gredi se ne upošteva
Primer reševanja problema napetosti-stiskanja palice
Naloga je preizkusiti trdnost jeklene palice pri danih dovoljenih napetostih. Med reševanjem se gradijo grafe vzdolžnih sil, normalnih napetosti in premikov. Lastna teža palice se ne upošteva
Uporaba izreka o ohranjanju kinetične energije
Primer reševanja problema uporabe izreka o ohranjanju kinetične energije mehanskega sistema
Določanje hitrosti in pospeška točke po danih enačbah gibanja
Primer reševanja problema določanja hitrosti in pospeška točke po danih enačbah gibanja
Določanje hitrosti in pospeška točk togega telesa med ravninsko vzporednim gibanjem
Primer reševanja problema določanja hitrosti in pospeška točk togega telesa med ravninsko vzporednim gibanjem
Določanje sil v ravninskih nosilnih palicah
Primer reševanja problema določanja sil v palicah ravne rešetke po Ritterjevi metodi in metodi rezanja vozla
državna avtonomna ustanova
Kaliningradska regija
strokovna izobraževalna organizacija
Visoka šola za storitve in turizem
Tečaj predavanj s primeri praktičnih nalog
"Osnove teoretične mehanike"
po discipliniTehnična mehanika
za študente3 seveda
posebnost20.02.04 Požarna varnost
Kaliningrad
ODOBRITE
Namestnik direktorja za SD GAU KO VEO KSTN.N. Myasnikov
ODOBREN
Metodološki svet GAU KO VET KST
UPOŠTEVAN
Na seji PCC
Uredniška ekipa:
Kolganova A.A., metodologinja
Falaleeva A.B., učiteljica ruskega jezika in književnosti
Cvetaeva L.V., predsednica PCCsplošne matematične in naravoslovne discipline
Sestavil:
Nezvanova I.V. Predavatelj GAU KO VET KST
Vsebina
Teoretični podatki
Teoretični podatki
Primeri reševanja praktičnih problemov
Dinamika: osnovni pojmi in aksiomi
Teoretični podatki
Primeri reševanja praktičnih problemov
Bibliografija
Teoretični podatki
Statika: osnovni pojmi in aksiomi.
Statika - del teoretične mehanike, ki obravnava lastnosti sil, ki delujejo na točke togega telesa, in pogoje za njihovo ravnotežje. Glavne naloge:
1. Preoblikovanje sistemov sil v enakovredne sisteme sil.
2. Določanje pogojev za ravnotežje sistemov sil, ki delujejo na togo telo.
materialna točka imenujemo najpreprostejši model materialnega telesa
katero koli obliko, katere dimenzije so dovolj majhne in jo je mogoče vzeti kot geometrijsko točko z določeno maso. Mehanski sistem je kateri koli niz materialnih točk. Popolnoma togo telo je mehanski sistem, katerega razdalje med točkami se ne spreminjajo pri nobeni interakciji.
Moč je merilo mehanske interakcije materialnih teles med seboj. Sila je vektorska količina, saj jo določajo trije elementi:
številčna vrednost;
smer;
točka uporabe (A).
Enota sile je Newton (N).

Slika 1.1
Sistem sil je niz sil, ki delujejo na telo.
Uravnotežen (enak nič) sistem sil je sistem, ki ob uporabi telesa ne spremeni svojega stanja.
Sistem sil, ki delujejo na telo, lahko nadomestimo z eno rezultanto, ki deluje kot sistem sil.
Aksiomi statike.
Aksiom 1: Če na telo uporabimo uravnotežen sistem sil, se giblje enakomerno in pravocrtno ali miruje (zakon vztrajnosti).
2. aksiom:
Absolutno togo telo je v ravnotežju pod delovanjem dveh sil, če in samo če sta ti sili po absolutni vrednosti enaki, delujeta v eni ravni črti in sta usmerjeni v nasprotni smeri. Slika 1.2
3. aksiom:
Mehansko stanje telesa ne bo moteno, če sistemu sil, ki nanj delujejo, dodamo ali odštejemo uravnotežen sistem sil.
4. aksiom: Rezultanta dveh sil, ki delujeta na telo, je enaka njuni geometrijski vsoti, to pomeni, da je izražena v absolutni vrednosti in smeri z diagonalo paralelograma, zgrajenega na teh silah kot na straneh.
Slika 1.3.
Aksiom 5:
Sile, s katerimi dve telesi delujeta drug na drugega, so po absolutni vrednosti vedno enake in usmerjene vzdolž ene premočrtne črte v nasprotni smeri.
Slika 1.4.
Vrste vezi in njihove reakcije
povezave
imenujemo vse omejitve, ki preprečujejo gibanje telesa v prostoru. Telo, ki se želi pod delovanjem uporabljenih sil premikati, kar mu preprečuje povezava, bo nanj delovalo z določeno silo, imenovano sila pritiska na povezavo
. Po zakonu enakosti delovanja in reakcije bo povezava delovala na telo z enakim modulom, vendar nasprotno usmerjeno silo.
Imenuje se sila, s katero ta povezava deluje na telo in preprečuje eno ali drugo gibanje reakcijska sila (reakcija) vezi
.
Eno od temeljnih načel mehanike je načelo osvoboditve
:
vsako nesvobodno telo lahko štejemo za prosto, če zavržemo vezi in njihovo delovanje nadomestimo z reakcijami vezi.
Reakcija vezi je usmerjena v nasprotni smeri, kjer vez ne dopušča premikanja telesa. Glavne vrste vezi in njihove reakcije so prikazane v tabeli 1.1.
Tabela 1.1
Vrste vezi in njihove reakcije
Ime komunikacije
1
Gladka površina (podpora)
- površina (podpora), trenje, na katerem lahko dano telo zanemarimo.
Z brezplačno podporo, reakcijaje usmerjena pravokotno na tangento skozi točkoAMPAK
telesni stik1
s podporno površino2
.

2
Nit (fleksibilna, neraztegljiva). Povezava, izdelana v obliki neraztegljive niti, ne omogoča, da se telo odmakne od točke vzmetenja. Zato je reakcija niti usmerjena vzdolž niti do točke njenega vzmetenja.

3
breztežna palica
– palica, katere težo lahko zanemarimo v primerjavi z zaznano obremenitvijo.
Reakcija breztežne zgibne premočrtne palice je usmerjena vzdolž osi palice.

4
Premični tečaj, zgibna premična podpora. Reakcija je usmerjena vzdolž normale na podporno površino.

7
Trdo zapiranje.
V ravnini toge vgradnje bosta dve komponenti reakcije,
in moment para sil, ki preprečuje obračanje žarka1
glede na točkoAMPAK
.
Toga pritrditev v prostoru telesu 1 odvzame vseh šest stopenj svobode - tri premike vzdolž koordinatnih osi in tri rotacije okoli teh osi.
V prostorski togi vgradnji bodo tri komponente,
,
in tri momente parov sil![]() .
.

Sistem konvergentnih sil
Sistem konvergentnih sil
imenujemo sistem sil, katerih linije delovanja se v eni točki sekajo. Dve sili, ki se zbližujeta v eni točki, lahko po tretjem aksiomu statike nadomestimo z eno silo -rezultat
.
Glavni vektor sistema sil
- vrednost, ki je enaka geometrijski vsoti sil sistema.
Rezultanta ravninskega sistema konvergentnih sil je mogoče določitigrafično in analitično.
Dodajanje sistema sil . Dodajanje ravnega sistema konvergentnih sil se izvede bodisi z zaporednim seštevanjem sil s konstrukcijo vmesne rezultante (slika 1.5), bodisi z izgradnjo poligona sil (slika 1.6).


Slika 1.5Slika 1.6
Projekcija sile na os
- algebraična količina, enaka zmnožku modula sile in kosinusa kota med silo in pozitivno smerjo osi.
ProjekcijaFx(sl.1.7) sile na os Xpozitivno, če je α akutno, negativno, če je α tupo. Če močje pravokotna na os, potem je njena projekcija na os enaka nič.

Slika 1.7
Projekcija sile na ravnino Ohu– vektor , sklenjena med projekcijama začetka in konca silena to letalo. tiste. projekcija sile na ravnino je vektorska količina, za katero ni značilna le številčna vrednost, temveč tudi smer v ravniniOhu (slika 1.8).

Slika 1.8
Nato projekcijski modul na letalo Ohu bo enako:
Fxy = F cosα,
kjer je α kot med smerjo sile in njegova projekcija.
Analitični način določanja sil
.
Za analitično metodo določanja siletreba je izbrati sistem koordinatnih osiOhz, glede na katerega bo določena smer sile v prostoru.
Vektor, ki prikazuje moč, je mogoče konstruirati, če so znani modul te sile in koti α, β, γ, ki jih tvori sila s koordinatnimi osmi. DotAMPAK uporaba sile ločeno po svojih koordinatahX,
pri,
z. Silo lahko nastavite z njenimi projekcijamifx,
fy,
fzna koordinatnih osih. Modul sile v tem primeru je določen s formulo:
![]()
in kosinus smeri:
,
.
Analitična metoda seštevanja sil : projekcija vektorja vsote na neko os je enaka algebraični vsoti projekcij členov vektorjev na isto os, t.j., če:
potem , , .
Poznavanje Rx, Ry, Rz, lahko definiramo modul
![]()
in kosinus smeri:
, , .
Slika 1.9
Za ravnotežje sistema konvergentnih sil je potrebno in zadostno, da je rezultanta teh sil enaka nič.1) Pogoj geometrijskega ravnotežja za konvergentni sistem sil : Za ravnotežje sistema konvergirajočih sil je potrebno in zadostno, da je poligon, zgrajen iz teh sil
je bil zaprt (konec vektorja zadnjega izraza
sila mora sovpadati z začetkom vektorja prvega člena sile). Potem bo glavni vektor sistema sil enak nič ()
2)
Pogoji analiznega ravnotežja
.
Modul glavnega vektorja sistema sil je določen s formulo.
![]() =0. V kolikor , potem je korenski izraz lahko enak nič le, če vsak člen hkrati izgine, t.j.
=0. V kolikor , potem je korenski izraz lahko enak nič le, če vsak člen hkrati izgine, t.j.
Rx= 0, Ry= 0, R z = 0.
Zato je za ravnotežje prostorskega sistema konvergentnih sil potrebno in zadostno, da so vsote projekcij teh sil na vsako od treh koordinat osi enake nič:
Za ravnotežje ravnega sistema konvergentnih sil je potrebno in zadostno, da je vsota projekcij sil na vsako od obeh koordinatnih osi enaka nič:
Seštevanje dveh vzporednih sil v isti smeri.

Slika 1.9
Dve vzporedni sili, usmerjeni v isto smer, se zmanjšata na eno rezultantno silo, vzporedno z njima in usmerjeno v isto smer. Velikost rezultante je enaka vsoti velikosti teh sil in točka njene uporabe C razdeli razdaljo med linijami delovanja sil znotraj na dele, ki so obratno sorazmerni z velikostjo teh sil, tj.B A C
R=F 1 +F 2
Seštevek dveh neenakih vzporednih sil, usmerjenih v nasprotni smeri.
Dve neenaki antiparalelni sili se zmanjšata na eno rezultantno silo, ki je vzporedna z njima in usmerjena proti večji sili. Velikost rezultante je enaka razliki med velikostmi teh sil, točka njenega delovanja, C, pa deli razdaljo med zunanjima linijama delovanja sil na dele, ki so obratno sorazmerni z velikostjo teh sil, tj. je
Par sil in moment sile okoli točke.
Trenutek sile
glede na točko O se imenuje z ustreznim predznakom produkt velikosti sile z razdaljo h od točke O do premice sile . Ta izdelek je vzet z znakom plus, če je sila teži k vrtenju telesa v nasprotni smeri urinega kazalca in z znakom -, če je sila teži k vrtenju telesa v smeri urinega kazalca, tj . Dolžina navpičnice h se imenujeramo moči
točka O. Učinek delovanja sile t.j. večji je kotni pospešek telesa, večja je velikost momenta sile.
Slika 1.11
Par sil Sistem imenujemo sistem, sestavljen iz dveh vzporednih sil enake velikosti, usmerjenih v nasprotni smeri. Razdalja h med linijama delovanja sil se imenujeramenski pari . Trenutek para sil m(F,F") je zmnožek vrednosti ene od sil, ki sestavljajo par, in kraka para, vzete z ustreznim predznakom.Zapiše se takole: m(F, F")= ± F × h, kjer je zmnožek vzet s predznakom plus, če se par sil nagiba k vrtenju telesa v nasprotni smeri urinega kazalca in z znakom minus, če se par sil teži za vrtenje telesa v smeri urinega kazalca.
Izrek o vsoti momentov sil para.
Vsota momentov sil para (F,F") glede na katero koli točko 0, vzeto v ravnini delovanja para, ni odvisna od izbire te točke in je enaka momentu para.
Izrek o enakovrednih parih. Posledice.
Izrek. Dva para, katerih momenti so med seboj enaki, sta enakovredna, t.j. (F, F") ~ (P, P")
Posledica 1 . Par sil je mogoče prenesti na katero koli mesto v ravnini njegovega delovanja, pa tudi zasukati na kateri koli kot in spremeniti roko in velikost sil para, pri tem pa ohraniti moment para.
Posledica 2. Par sil nima rezultante in ga ni mogoče uravnotežiti z eno silo, ki leži v ravnini para.

Slika 1.12
Seštevanje in ravnotežni pogoj za sistem parov na ravnini.
1. Izrek o seštevanju parov, ki ležijo v isti ravnini. Sistem parov, poljubno nameščenih v isti ravnini, lahko nadomestimo z enim parom, katerega moment je enak vsoti momentov teh parov.
2. Izrek o ravnotežju sistema parov na ravnini.
Da absolutno togo telo miruje pod delovanjem sistema parov, poljubno nameščenih v isti ravnini, je potrebno in zadostno, da je vsota momentov vseh parov enaka nič, tj.
Težišče
Sila gravitacije - rezultanta privlačnih sil na Zemljo, razporejenih po celotnem volumnu telesa.
Težišče telesa - to je taka točka, ki je vedno povezana s tem telesom, skozi katero poteka linija delovanja sile gravitacije danega telesa v katerem koli položaju telesa v prostoru.
Metode za iskanje težišča
1. Metoda simetrije:
1.1. Če ima homogeno telo simetrično ravnino, potem težišče leži v tej ravnini
1.2. Če ima homogeno telo simetrično os, potem težišče leži na tej osi. Težišče homogenega vrtilnega telesa leži na osi vrtenja.
1.3 Če ima homogeno telo dve simetrični osi, je težišče na točki njunega preseka.
2. Metoda razdelitve: Telo je razdeljeno na najmanjše število delov, katerih sile teže in položaj težišč so znane.
3. Metoda negativnih mas: Pri določanju težišča telesa s prostimi votlinami je treba uporabiti metodo razdelitve, vendar je treba maso prostih votlin šteti za negativno.
Koordinate težišča ravne figure:

Položaje težišč preprostih geometrijskih figur je mogoče izračunati z uporabo dobro znanih formul. (Slika 1.13)

Opomba: Težišče simetrije figure je na osi simetrije.
Težišče palice je na sredini višine.
1.2. Primeri reševanja praktičnih problemov
Primer 1:
Utež je obešena na palici in je v ravnotežju. Določite sile v palici. (Slika 1.2.1)
rešitev:
Sile, ki nastanejo v pritrdilnih palicah, so po velikosti enake silam, s katerimi palice podpirajo obremenitev. (5. aksiom)
Določimo možne smeri reakcij vezi "toge palice".
Prizadevanja so usmerjena vzdolž palic.
Slika 1.2.1.
Točko A osvobodimo vezi in zamenjamo delovanje vezi z njihovimi reakcijami. (Slika 1.2.2)
Začnimo konstrukcijo z znano silo, tako da narišemo vektorFv nekem obsegu.
Od konca vektorjaFnarišite črte, vzporedne z reakcijamiR 1 inR 2 .
Slika 1.2.2
Črte, ki se križajo, tvorijo trikotnik. (Slika 1.2.3.). Če poznamo merilo konstrukcij in izmerimo dolžino stranic trikotnika, je mogoče določiti velikost reakcij v palicah.
Za natančnejše izračune lahko uporabite geometrijske odnose, zlasti sinusni izrek: razmerje med stranico trikotnika in sinusom nasprotnega kota je konstantna vrednost
![]()
za ta primer:
Slika 1.2.3
![]()
Komentar: Če se smer vektorja (reakcija spajanja) na dani shemi in v trikotniku sil ne ujema, bi morala biti reakcija na shemi usmerjena v nasprotno smer.
2. primer:
Na analitični način določite velikost in smer nastalega ploščatega sistema konvergentnih sil.
rešitev:
Slika 1.2.4
1. Določimo projekcije vseh sil sistema na Ox (slika 1.2.4)Z algebračnim seštevanjem projekcij dobimo projekcijo rezultante na os Ox.

Znak označuje, da je rezultanta usmerjena v levo.
2. Določimo projekcije vseh sil na os Oy:
Če algebraično seštejemo projekcije, dobimo projekcijo rezultante na os Oy.
Znak označuje, da je rezultanta usmerjena navzdol.
3. Določite modul rezultante z velikostmi projekcij:
4. Določite vrednost kota rezultante z osjo Ox:
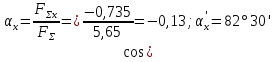
in vrednost kota z osjo y:

3. primer:
Izračunajte vsoto momentov sil glede na točko O (slika 1.2.6).
OA= AB= IND=DE=CB=2m
Slika 1.2.6
rešitev:
1. Moment sile glede na točko je številčno enak zmnožku modula in kraka sile.
2. Moment sile je enak nič, če poteka črta delovanja sile skozi točko.
4. primer:
Določite položaj težišča slike, prikazane na sliki 1.2.7
rešitev:
Sliko razdelimo na tri:
1-pravokotnik
AMPAK 1 =10*20=200 cm 2
2-trikotnik
AMPAK 2 =1/2*10*15=75 cm 2
3-krog
AMPAK 3 =3,14*3 2 = 28,3 cm 2
Slika 1 CG: x 1 =10 cm, y 1 = 5 cm
Slika 2 CG: x 2 =20+1/3*15=25cm, u 2 =1/3*10=3,3 cm
Slika 3 CG: x 3 =10 cm, y 3 = 5 cm
Podobno je opredeljen za od = 4,5 cm
Kinematika: osnovni pojmi.
Osnovni kinematični parametri
Pot - črta, ki jo začrta materialna točka, ko se premika v prostoru. Pot je lahko ravna črta in krivulja, ravna in prostorska črta.
Enačba poti za gibanje ravnine: y =f ( x)
Prevožena razdalja. Pot se meri vzdolž poti v smeri vožnje. Oznaka -S, merske enote - metri.
Enačba gibanja točke je enačba, ki določa položaj gibljive točke kot funkcijo časa.
Slika 2.1
Položaj točke v vsakem trenutku je mogoče določiti z razdaljo, prevoženo vzdolž trajektorije od neke fiksne točke, ki se šteje za izhodišče (slika 2.1). Takšno gibanje se imenujenaravno . Tako lahko enačbo gibanja predstavimo kot S = f (t).

Slika 2.2
Položaj točke lahko določimo tudi, če poznamo njene koordinate kot funkcijo časa (slika 2.2). Nato je treba v primeru gibanja po ravnini podati dve enačbi:V primeru prostorskega gibanja se doda še tretja koordinataz= f 3 ( t)
Takšno gibanje se imenujekoordinirati .
Potovalna hitrost je vektorska količina, ki označuje trenutno hitrost in smer gibanja vzdolž poti.
Hitrost je vektor, usmerjen v vsakem trenutku tangencialno na trajektorijo proti smeri gibanja (slika 2.3).
Slika 2.3
Če točka v enakih časovnih intervalih pokriva enake razdalje, se imenuje gibanjeuniforma .Povprečna hitrost na poti ΔSopredeljeno:
kje∆S- prevožena razdalja v času Δt; Δ t- časovni interval.
Če točka v enakih časovnih intervalih prepotuje neenake poti, se gibanje imenujeneenakomerno . V tem primeru je hitrost spremenljiva in odvisna od časav= f( t)
Trenutna hitrost je definirana kot
točkovni pospešek - vektorska količina, ki označuje hitrost spremembe hitrosti v velikosti in smeri.
Hitrost točke pri premikanju od točke M1 do točke Mg se spremeni po velikosti in smeri. Povprečna vrednost pospeška za to časovno obdobje
Trenutni pospešek:
Običajno se zaradi udobja upoštevata dve medsebojno pravokotni komponenti pospeška: normalna in tangencialna (slika 2.4)
Normalni pospešek a n , označuje spremembo hitrosti za
smer in je opredeljena kot
Normalni pospešek je vedno usmerjen pravokotno na hitrost proti središču loka.
Slika 2.4
Tangencialni pospešek a t , označuje spremembo hitrosti v velikosti in je vedno usmerjen tangencialno na trajektorijo; pri pospeševanju njegova smer sovpada s smerjo hitrosti, pri pojemku pa je usmerjena nasprotno smeri vektorja hitrosti.![]()
Vrednost celotnega pospeška je opredeljena kot:
Analiza vrst in kinematičnih parametrov gibanj
Enotno gibanje - To je gibanje s konstantno hitrostjo:
Za pravokotno enakomerno gibanje:
Za ukrivljeno enakomerno gibanje:
![]()
Zakon enakomernega gibanja :
Enako spremenljivo gibanje – je gibanje s konstantnim tangencialnim pospeškom:
Za pravokotno enakomerno gibanje
Za ukrivljeno enakomerno gibanje:
![]()
Zakon enakomernega gibanja:
![]()
Kinematični grafi
Kinematični grafi - To so grafi sprememb poti, hitrosti in pospeška, odvisno od časa.
Enotno gibanje (slika 2.5)

Slika 2.5
Enako spremenljivo gibanje (slika 2.6)

Slika 2.6
Najpreprostejši gibi togega telesa
Gibanje naprej imenujemo gibanje togega telesa, pri katerem vsaka ravna črta na telesu med gibanjem ostane vzporedna s svojim začetnim položajem (slika 2.7)

Slika 2.7
Pri translacijskem gibanju se vse točke telesa premikajo na enak način: hitrosti in pospeški so v vsakem trenutku enaki.
Prirotacijskega gibanja
vse točke telesa opisujejo kroge okoli skupne fiksne osi.
Imenuje se fiksna os, okoli katere se vrtijo vse točke telesaos vrtenja.
Samo za opis rotacijskega gibanja telesa okoli fiksne osikotne možnosti. (Slika 2.8)
φ je kot vrtenja telesa;
ω – kotna hitrost, določa spremembo kota vrtenja na enoto časa;
Sprememba kotne hitrosti s časom je določena s kotnim pospeškom:
2.2. Primeri reševanja praktičnih problemov
Primer 1: Podana je enačba gibanja točke. Določite hitrost točke na koncu tretje sekunde gibanja in povprečno hitrost prve tri sekunde.
![]()
rešitev:
1. Enačba hitrosti
2. Hitrost ob koncu tretje sekunde (t=3 c)
3. Povprečna hitrost
2. primer: Po podanem zakonu gibanja določite vrsto gibanja, začetno hitrost in tangencialni pospešek točke, čas ustavljanja.
![]()
rešitev:
1. Vrsta gibanja: enako spremenljivo (![]() )
)
2. Pri primerjavi enačb je očitno, da
- začetna pot, prevožena pred začetkom odštevanja 10m;
- začetna hitrost 20m/s
- konstantni tangencialni pospešek ![]()
- pospešek je negativen, zato je gibanje počasno, pospešek je usmerjen v nasprotno smer od hitrosti gibanja.
3. Določite lahko čas, ko bo hitrost točke enaka nič.
3. Dinamika: osnovni pojmi in aksiomi
Dinamika - odsek teoretične mehanike, v katerem se vzpostavi povezava med gibanjem teles in silami, ki nanje delujejo.
V dinamiki se rešujeta dve vrsti problemov:
določiti parametre gibanja glede na dane sile;
določi sile, ki delujejo na telo, glede na dane kinematične parametre gibanja.
Spodajmaterialna točka
pomenijo določeno telo, ki ima določeno maso (tj. vsebuje določeno količino snovi), vendar nima linearnih dimenzij (neskončno majhen volumen prostora).
Izolirana
upošteva se materialna točka, na katero druge materialne točke ne vplivajo. V resničnem svetu izolirane materialne točke, pa tudi izolirana telesa, ne obstajajo, ta koncept je pogojen.
Pri translacijskem gibanju se vse točke telesa premikajo na enak način, zato lahko telo vzamemo kot materialno točko.
Če so dimenzije telesa majhne v primerjavi s potjo, ga lahko štejemo tudi za materialno točko, medtem ko točka sovpada s težiščem telesa.
Med rotacijskim gibanjem telesa se točke morda ne premikajo na enak način, v tem primeru lahko nekatere določbe dinamike uporabimo le za posamezne točke, materialni predmet pa lahko obravnavamo kot množico materialnih točk.
Zato se dinamika deli na dinamiko točke in dinamiko materialnega sistema.
Aksiomi dinamike
Prvi aksiom ( načelo vztrajnosti): v katera koli izolirana materialna točka je v stanju mirovanja ali enakomernega in pravokotnega gibanja, dokler je uporabljene sile ne vzamejo iz tega stanja.
To stanje se imenuje državavztrajnost. Odstranite točko iz tega stanja, t.j. dajte mu nekaj pospeška, morda zunanjo silo.
Vsako telo (točka) imavztrajnost. Merilo vztrajnosti je masa telesa.
maša poklicalkoličino snovi v telesu v klasični mehaniki velja za konstantno vrednost. Enota mase je kilogram (kg).
Drugi aksiom (Newtonov drugi zakon je osnovni zakon dinamike)
F=ma
kjeT - masa točke, kg;ampak - točkovni pospešek, m/s 2 .
Pospešek, ki ga materialni točki daje sila, je sorazmeren z velikostjo sile in sovpada s smerjo sile.
Gravitacija deluje na vsa telesa na Zemlji, daje telesu pospešek prostega pada, usmerjenega proti središču Zemlje:
G = mg
kjeg- 9,81 m/s², pospešek prostega padca.
Tretji aksiom (Newtonov tretji zakon): sSile medsebojnega delovanja dveh teles so enake po velikosti in usmerjene vzdolž iste premice v različne smeri.
Pri interakciji so pospeški obratno sorazmerni z masami.
Četrti aksiom (zakon neodvisnosti delovanja sil): toVsaka sila sistema sil deluje tako, kot bi delovala sama.
Pospešek, ki ga točki daje sistem sil, je enak geometrijski vsoti pospeškov, ki jih točki daje vsaka sila posebej (slika 3.1):

Slika 3.1
Koncept trenja. Vrste trenja.
Trenje-
upor, ki nastane zaradi gibanja enega grobega telesa po površini drugega. Drsno trenje povzroči drsno trenje, kotalno trenje pa trenje zibanja.
Drsno trenje
Slika 3.2.
Razlog je mehanski vprijem izrastkov. Sila upora proti gibanju med drsenjem se imenuje sila drsnega trenja (slika 3.2)Zakoni drsnega trenja:
1. Sila drsnega trenja je neposredno sorazmerna s silo normalnega tlaka: 
kjeR- sila normalnega tlaka, usmerjena pravokotno na podporno površino;f- koeficient drsnega trenja.
Slika 3.3.
V primeru, da se telo premika po nagnjeni ravnini (slika 3.3)kotalno trenje
Kotalni upor je povezan z medsebojno deformacijo tal in kolesa in je veliko manjši od trenja drsenja.
Za enakomerno kotaljenje kolesa je potrebno uporabiti siloF dv (Slika 3.4)
Pogoj kotalnega kolesa je, da premični moment ne sme biti manjši od upornega momenta:
Slika 3.4.
Primer 1: 2. primer: Na dve materialni točki masem 1 = 2 kg inm 2 = delujejo enake sile 5 kg. Hitreje primerjajte vrednosti.rešitev:
Po tretjem aksiomu je dinamika pospeška obratno sorazmerna z masami: ![]()
3. primer:
Določite delo teže pri premikanju bremena od točke A do točke C po nagnjeni ravnini (slika 3. 7). Sila težnosti telesa je 1500N. AB=6m, BC=4m. 3. primer:
Določite delo rezalne sile v 3 minutah. Hitrost vrtenja dela je 120 vrt/min, premer obdelovanca je 40 mm, rezalna sila je 1 kN. (Slika 3.8)
rešitev:
1. Delo z rotacijskim gibanjem:
2. Kotna hitrost 120 vrt./min
Slika 3.8.
3. Število vrtljajev za določen čas jez\u003d 120 * 3 \u003d 360 vrt.Kot vrtenja v tem času φ=2πz\u003d 2 * 3,14 * 360 \u003d 2261 rad
4. Delajte 3 obrate:W\u003d 1 * 0,02 * 2261 \u003d 45,2 kJ
Bibliografija
Olofinskaya, V.P. "Tehnična mehanika", Moskva "Forum" 2011
Erdedi A.A. Erdedi N.A. Teoretična mehanika. Trdnost materialov.- R-n-D; Phoenix, 2010